Bài 3. Phép cộng và phép trừ hai số nguyên (Phần 2: Bài 7 đến Bài 12) trang 52 Vở bài tập toán lớp 6 tập 1 NXB Chân Trời Sáng Tạo
\(7\). Tính nhanh các tổng sau:
a) \((67-5759) + 5759; \)
b) \((- 3023) – (765 – 3023); \)
c) \(631 + [587-(287 + 231)]; \)
d) \((-524)-[(476 + 245)-45].\)
Giải
a)
\((67-5759) + 5759\)
\(= 67 + (– 5759) + 5759\)
\(= 67.\)
b)
\((-3023)-(765-3023)\)
\(= (-3023)-765 + 3023\)
\(= (-3023) + 3023 + (– 765)\)
\(=-765.\)
c)
\(631 + [587-(287 + 231)]\)
\(= 631 + 587-287-231\)
\(= 631-231 + 587-287\)
\(= 400 + 300\)
\(=700.\)
d)
\((-524)-[(476 + 245)-45]\)
\(= (-524)-476-245 + 45\)
\(= (-524) + (– 476) + (– 245) + 45\)
\(=-(524+476)-(245-45)\)
\(=-1000-200\)
\(=-1200.\)
\(\)
\(8\). Thuỷ ngân là một kim loại ở thể lỏng trong điều kiện nhiệt độ thông thường. Nhiệt độ nóng chảy của thuỷ ngân là \(–39^\text{o}C.\) Nhiệt độ sôi của thuỷ ngân là \(357^\text{o}C.\) Tính số độ chênh lệch giữa nhiệt độ sôi và nhiệt độ nóng chảy của thuỷ ngân.
Giải
Số độ chênh lệch giữa nhiệt độ sôi và nhiệt độ nóng chảy của thuỷ ngân là:
\(357–(–39) = 357 + 39 = 396^{\text{o}}C.\)
\(\)
\(9\). Vào một buổi trưa nhiệt độ ở New York (Niu Oóc) là \(–5^\text{o}C.\) Nhiệt độ đêm hôm đó ở New York là bao nhiêu, biết nhiệt độ đêm đó giảm \(7^\text{o}C?\)
Giải
Nhiệt độ đêm hôm đó ở New York là \(-5-7 = -12^\text{o}C.\)
\(\)
\(10\). Tính tổng các số nguyên \(x\) thoả mãn mỗi điều kiện sau:
a) \(−7<x<8;\)
b) \(−10<x<9;\)
c) \(−12<x<12;\)
d) \(−15≤x<15.\)
Giải
a)
Ta có: \(−7\lt x \lt8 \Rightarrow x =\{−6;−5;…;7\}.\)
Tổng của chúng là \(T = (-6) + (-5) + (-4) + \cdots + 4 + 5 + 6 + 7\)
\(= (-6) + 6 + (-5) + 5 + (-4) + 4 + \cdots + 0 + 7= 7.\)
b)
Ta có: \(−10\lt x \lt9 \Rightarrow x =\{−9;−8;…;−1;0;1;…;8\}.\)
Tổng của chúng là \(T = (-9) + (-8) + \cdots + (-1) + 0 + 1 + \cdots + 8\)
\(= (-9) + (-8) + 8 + (-7) + 7 + \cdots + (-1) + 1 + 0= -9.\)
c)
Ta có: \(−12\lt x \lt12 \Rightarrow x =\{−11;−10;…;−1;0;1;…;11\}.\)
Tổng của chúng là \(T = (-11) + \cdots + (-1) + 0 + 1 + \cdots + 11\)
\(= (-11) + 11 + (-10) + 10 + \cdots + (-1) + 1= 0.\)
d)
Ta có: \(−15 \le x\lt15 \Rightarrow x =\{−15;−14;−13;…;−1;0;1;…;14\}.\)
Tổng của chúng là \(T = (-15) + (-14) + (-13) + (-12) + \cdots + 12 + 13 + 14= -15.\)
\(\)
\(11\). Trong bóng đá, nhiều trường hợp để xếp hạng các đội bóng sau một mùa giải, người ta phải tính kết quả của hiệu số bàn thắng – thua. Hãy tính hiệu số bàn thắng – thua của các đội bóng đá nam trong bảng dưới đây.
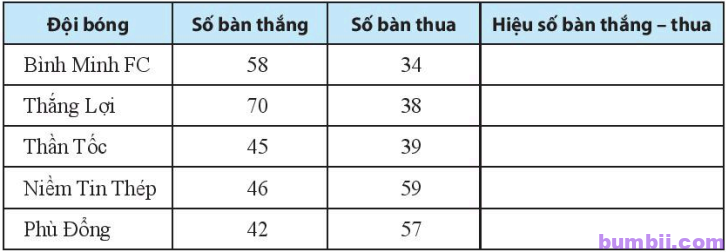
Giải
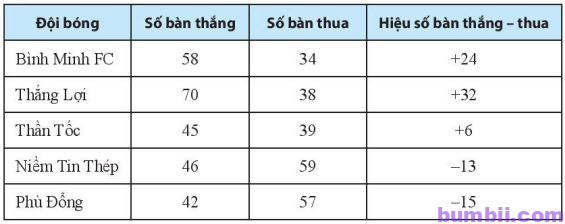
\(\)
\(12\). Hai số nguyên có một chữ số có tổng bằng \(-9.\) Hãy tìm hai số đó. Bài toán có bao nhiêu đáp số?
Giải
Gọi \(2\) số nguyên cần tìm là \(a\) và \(b,\) với \(a,b \in \mathbb{Z}.\)
Nếu có một số là số nguyên dương, giả sử \(a > 0\). Khi đó \(b = -9-a =-(9 +a)\) là số có nhiều hơn một chữ số \( \Rightarrow a,b \in \{−9;−8;…;0\}.\)
Mặt khác, ta có \(-9 = (-9) + 0 = (-8) + (-1) = (-7) + (-2) = (-6) + (-3) = (-5) + (-4).\)
Vậy hai số nguyên đó là \(-9\) và \(0;\) \(-8\) và \(-1;\) \(-7\) và \(-2;\) \(-6\) và \(-3;\) \(-5\) và \(-4.\)
\(\)
Xem bài giải trước: Bài 3. Phép cộng và phép trừ hai số nguyên (Phần 1: Bài 1 đến Bài 6)
Xem bài giải tiếp theo: Bài 4. Phép nhân và phép chia hết hai số nguyên
Xem các bài giải khác: Giải bài tập Toán Lớp 6 – NXB Chân Trời Sáng Tạo

Đường tuy ngắn không đi không đến; Việc tuy nhỏ không làm không nên.