Chương \(4\) – Bài \(4\): Định lí và chứng minh định lí trang \(86\) vở bài tập toán lớp \(7\) tập \(1\) NXB Chân Trời Sáng Tạo.
\(1.\) Ta gọi hai góc có tổng bằng \(180^o\) là hai góc bù nhau. Hãy viết giả thiết, kết luận bằng kí hiệu và chứng minh định lí: “Hai góc cùng bù một góc thứ ba thì hai góc đó bằng nhau”.
Giải
Viết giả thiết và kết luận:

Chứng minh định lí:
Theo GT ta có:
\(\widehat{A}\) và \(\widehat{C}\) là hai góc bù nhau. Suy ra \(\widehat{A} + \widehat{C} = 180^o.\) Vậy \(\widehat{A} = 180^o – \widehat{C};\) \((1)\)
\(\widehat{B}\) và \(\widehat{C}\) là hai góc bù nhau. Suy ra \(\widehat{B} + \widehat{C} = 180^o.\) Vậy \(\widehat{B} = 180^o – \widehat{C}.\) \((2)\)
Từ \((1)\) và \((2)\) suy ra kết luận \(\widehat{A} = \widehat{B}.\)
\(\)
\(2.\) Cho định lí “Hai góc đối đỉnh thì bằng nhau”.
a) Hãy vẽ hình minh hoạ, phát biểu giả thiết của định lí trên.
b) Hãy chứng minh định lí đó.
Giải
a) Hình minh họa:
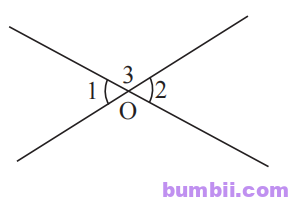
Viết giả thiết kết luận:
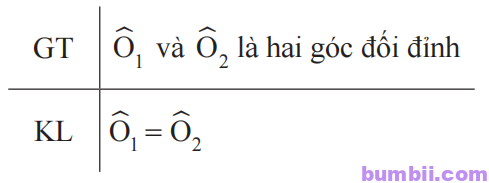
b) Chứng minh định lí:
Theo GT ta có
\(\widehat{O_1}\) và \(\widehat{O_3}\) là hai góc kề bù. Suy ra \(\widehat{O_1} + \widehat{O_3} = 180^o.\) Vậy \(\widehat{O_1} = 180^o – \widehat{O_3};\) \((1)\)
\(\widehat{O_2}\) và \(\widehat{O_3}\) là hai góc kề bù. Suy ra \(\widehat{O_2} + \widehat{O_3} = 180^o.\) Vậy \(\widehat{O_2} = 180^o – \widehat{O_3}.\) \((2)\)
Từ \((1)\) và \((2)\) suy ra kết luận \(\widehat{O_1} = \widehat{O_2}.\)
\(\)
\(3.\) Chứng minh định lí: “Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông”.
Giải
Hình minh họa:
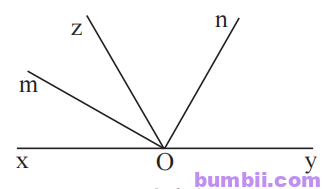
Viết giả thiết kết luận:

Chứng minh:
Vì Om là tia phân giác của \(\widehat{xOz}\) nên \(\widehat{xOm} = \widehat{mOz} = \displaystyle\frac{\widehat{xOz}}{2}.\ (1)\)
Vì Om là tia phân giác của \(\widehat{zOy}\) nên \(\widehat{zOn} = \widehat{nOy} = \displaystyle\frac{\widehat{zOy}}{2}.\ (2)\)
Từ \(1\) và \(2\) ta có \(\widehat{mOz} = \widehat{zOn} = \displaystyle\frac{1}{2}(\widehat{xOz} + \widehat{zOy}).\)
Suy ra \(\widehat{mOz} + \widehat{zOn} = \displaystyle\frac{1}{2}.180^o = 90^o\) (vì \(\widehat{xOz}\) và \(\widehat{zOy}\) là hai góc kề bù)
Hay \(\widehat{mOn} = 90^o.\)
\(\)
\(4.\) Chứng minh định lí: “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau”.
Giải
Hình minh họa:
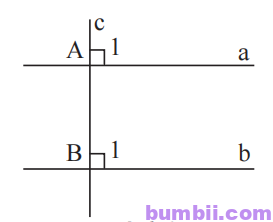
Viết giả thiết kết luận:

Chứng minh:
Ta có \(a \bot c\) suy ra \(\widehat{A_1} = 90^o\) và \(b \bot c\) suy ra \(\widehat{B_1} = 90^o.\) Vậy \(\widehat{A_1} = \widehat{B_1}.\)
Mà hai góc \(\widehat{A_1},\ \widehat{B_1}\) là hai góc đồng vị. Suy ra a//b.
\(\)
\(5.\) Hãy phát biểu phần kết luận còn thiếu của các định lí sau:
a) Hai góc cùng phụ một góc thứ ba thì .?.
b) Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì .?.
Giải
a) Hai góc cùng phụ một góc thứ ba thì bằng nhau.
b) Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì hai đường thẳng đó song song với nhau.
\(\)
Xem bài giải trước: Bài 3: Hai đường thẳng song song
Xem bài giải tiếp theo: Bài tập cuối chương 4
Xem thêm các bài giải khác tại: Giải Bài tập Toán Lớp 7 – NXB Chân Trời Sáng Tạo
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech
