Chương \(3\) – Bài \(2\): Diện tích xung quanh và thể tích của hình hộp chữ nhật, hình lập phương trang \(53\) vở bài tập toán lớp \(7\) tập \(1\) NXB Chân Trời Sáng Tạo.
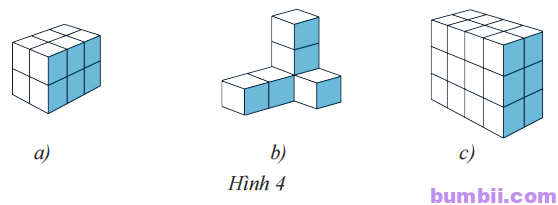
\(1.\) Biết mỗi khối đơn vị có thể tích \(1 cm^3\). Tính thể tích các khối trong Hình \(4\).
Giải
a) Hình \(4\ a),\) có \(12\) khối đơn vị, thể tích của khối hộp là: \(12.1\ cm^3=12\ cm^3\).
b) Hình \(4\ b),\) có \(6\) khối đơn vị, thể tích của khối hộp là \(6.1\ cm^3=6\ cm^3\).
c) Hình \(4\ c)\), có \(24\) khối đơn vị, thể tích của khối hộp là \(24.1\ cm^3=24\ cm^3\).
\(\)
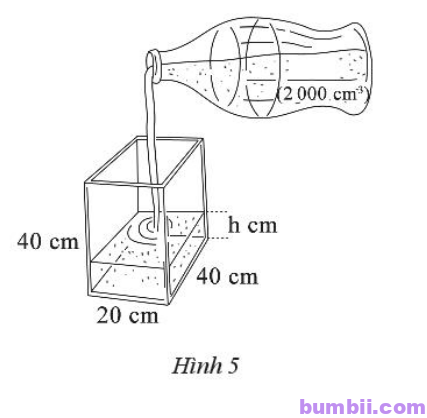
\(2.\) Một cái bể hình hộp chữ nhật và một cái chai có kích thước và thể tích như Hình \(5.\) Cho biết một chai nước đầy rót hết vào bể.
a) Tính thể tích của cái bể.
b) Tính chiều cao mực nước sau khi rót hết một chai nước vào bể.
c) Nếu rót đầy bể thì cần bao nhiêu chai nước.
Giải
a)Thể tích của bể là: \(V = 20 . 40 . 40 = 32 000\ (cm^3).\)
b) Chiều cao của mực nước sau khi rót hết một chai nước là:
\(h = \displaystyle\frac{V_{chai \ nước}}{S} = \displaystyle\frac{2000}{20.40}=2,5\ (cm).\)
c) Số chai nước là: \(32\ 000 : 2\ 000 = 16\) (chai).
\(\)
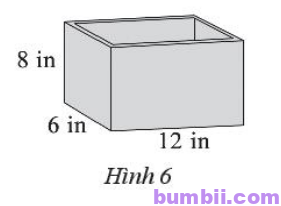
\(3.\) Một cái bể có kích thước như Hình \(6.\) Bề dày bể cả bốn phía và đáy là \(\displaystyle\frac{1}{4}\) inch. Tính thể tích của bể.
Giải
Chiều rộng của lòng bể (không kể phần thành bể) là: \(6-\displaystyle\frac{1}{4}-\displaystyle\frac{1}{4} = \displaystyle\frac{11}{2}\) (in).
Chiều dài của lòng bể (không kể phần thành bể) là: \(12 – \displaystyle\frac{1}{4} – \displaystyle\frac{1}{4} =\displaystyle\frac{23}{2}\)(in).
Chiều cao của lòng bể (không kể phần thành bể) là: \(8-\displaystyle\frac{1}{4} = \displaystyle\frac{31}{4}\) (in). (do bể không có nắp nên ta chỉ cần trừ đi bề dày của phần đáy bể).
Thể tích của bể là: V = \(\displaystyle\frac{11}{2}.\displaystyle\frac{23}{2}.\displaystyle\frac{31}{4}=\displaystyle\frac{7843}{16} =490,1875\ (in^3).\)
\(\)
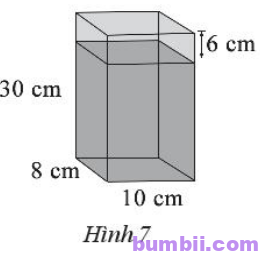
\(4.\) Một bình hình lăng trụ có kích thước đáy và chiều cao như Hình \(7.\) Nam đổ vào đó một lượng nước, rồi đo khoảng cách từ mực nước sau khi đổ tới miệng bình được \(6\) cm. Số lít nước đổ vào là bao nhiêu?
Giải
Chiều cao của mực nước đổ vào bình là: \(30 – 6 = 24\) (cm).
Thể tích phần mực nước đổ vào bình là: \(V = 8 . 10 . 24 = 1 920\) (cm3).
Đổi: \(1 920\ cm^3 = 1,92 \ dm^3 = 1,92\) lít.
Vậy số lít nước đổ vào bình là \(1,92\) lít.
\(\)
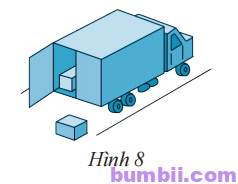
\(5.\) Một chiếc xe chở hàng có kích thước thùng xe là \(19\) ft, \(8\) ft và \(8\) ft (Hình \(8\)) (\(1\) fl \(\approx 30,48\) cm). Một thùng hàng có kích thước \(2\) ft, \(2\) ft và \(1\) ft. Thùng xe có thể chở tối đa bao nhiêu thùng hàng nếu biết cách sắp xếp hợp lí.
Giải
Thùng xe và thùng hàng đều có dạng hình hộp chữ nhật.
Thể tích của thùng xe là: \(V = 19 . 8 . 8 = 1\ 216 \ (ft^3).\)
Thể tích của một thùng hàng là: \(v = 2 . 2 . 1 = 4 \ (ft^3).\)
Số thùng hàng có thể chở nếu biết cách sắp xếp hợp lí là: \(1\ 216 : 4 = 304\) (thùng).
Ta có thể xếp trong thùng xe thành \(8\) dãy thùng hàng, mỗi dãy gồm \(38\) thùng hàng.
\(\)
\(6.\) Một bể cá có kích thước đáy \(1\) m, \(0,5\) m (Hình \(9\)), chiều cao mực nước cho phép là \( 0,4\) m. Một cái can có dung tích \(10\) lít, hỏi đổ bao nhiêu can nước thì tới mực nước cho phép?

Giải
Thể tích bể có chiều cao từ đáy tới mực nước cho phép là:
\(V = 1\ .\ 0,5\ .\ 0,4\ =\ 0,2 \ (m^3) = 200\) (lít).
Số can nước là: \(200 : 10 = 20\) (can).
\(\)
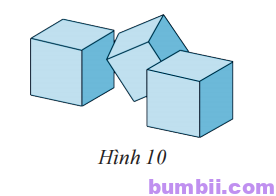
\(7.\) Bạn Nam có \(20\) khối lập phương cạnh \(4\) cm (Hình \(10\)), các khối lập phương này phải được đóng vào hộp để chuyển đi cho Khánh. Mỗi hộp có kích thước \(8\) cm, \(10\) cm, \(8\) cm. Phải cần bao nhiêu hộp để đóng cho đủ \(20\) khối lập phương trên?
Giải
Mỗi hộp chứa tối đa được: \(8\) khối lập phương.
Mà \(20 : 8 = 2\) còn dư \(4.\)
Vậy cần \(3\) chiếc hộp để chứa \(20\) khối lập phương.
\(\)
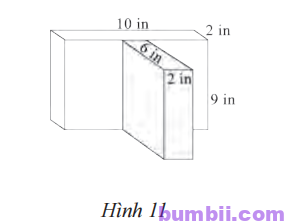
\(8.\) Hai hình hộp chữ nhật được ghép với nhau như Hình \(11.\)
a) Tính thể tích của khối ghép.
b) Tính diện tích toàn phần của khối ghép.
Giải
a) Khối hộp chữ nhật phía sau có kích thước \(10\) in, \(2\) in, \(9\) in nên có thể tích là:
\(V_1 = 10 . 2 . 9 = 180\ (in^3).\)
Khối hộp chữ nhật phía trước có kích thước 6 in, 2 in, 9 in nên có thể tích là:
\(V_2 = 6 . 2 . 9 = 108\ (in^3).\)
Hai khối hộp chữ nhật được ghép lại như Hình 11 có thể tích là:
\(V = V_1 + V_2 = 180 + 108 = 288\ (in^3).\)
b) Diện tích toàn phần của khối ghép bằng tổng diện tích toàn phần của hai khối trừ đi hai lần diện tích mặt tiếp xúc nhau.
Diện tích toàn phần của khối hộp chữ nhật bằng tổng diện tích xung quanh và diện tích \(2\) đáy.
Diện tích toàn phần của khối hộp chữ nhật phía sau là:
\(S_1 = 2 . (10 + 2) . 9 + 2 . 10 . 2 = 256\ (in^2).\)
Diện tích toàn phần của khối hộp chữ nhật phía trước là:
\(S_2 = 2 . (6 + 2) . 9 + 2 . 6 . 2 = 168\ (in^2).\)
Phần tiếp xúc nhau của hai khối hộp trên là một hình chữ nhật có kích thước là \(2\) in và \(9\) in.
Diện tích toàn phần của khối ghép là:
\(S = (S_1 + S_2) – 2 . 2 . 9\) \(= (256 + 168) – 36 = 388\ (in^2).\)
\(\)
Xem bài giải trước: Bài 1: Hình hộp chữ nhật – Hình lập phương
Xem bài giải tiếp theo: Bài 3: Hình lăng trụ đứng tam giác – Hình lăng trụ đứng tứ giác
Xem thêm các bài giải khác tại: Giải Bài tập Toán Lớp 7 – NXB Chân Trời Sáng Tạo
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech
