Bài 10. Số nguyên tố. Hợp số. Phân tích một số ra thừa số nguyên tố (Phần 1: Bài 1 đến Bài 5) trang 28 Vở bài tập toán lớp 6 tập 1 NXB Chân Trời Sáng Tạo
\(1\). Gọi \(P\) là tập hợp các số nguyên tố. Điền kí hiệu \(\in, \notin\) thích hợp vào chỗ chấm.
\(41\) … \(P\);
\(57\) … \(P\);
\(83\) … \(P\);
\(95\) … \(P\).
Giải
\(41\in P\);
\(57\notin P\) vì \(57\) có thể chia hết cho \(3\);
\(83\in P\);
\(95\notin P\) vì \(95\) có thể chia hết cho \(5\).
\(\)
\(2\). Dùng bảng nguyên tố tìm các số nguyên tố trong các số sau:
\(117;131;313;469;647.\)
Giải
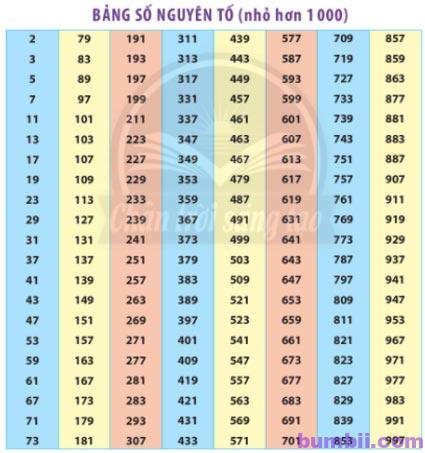
Tra bảng ta được \(131;313;647\) là các số nguyên tố.
\(\)
\(3\). Thay chữ số thích hợp vào dấu * để được mỗi số sau là:
a) hợp số: \(\overline{2∗};\overline{3∗}.\)
b) số nguyên tố: \(\overline{1∗};\overline{4∗}.\)
Giải
a)
Lần lượt thay \(*\) thành \(0,1,2,4,5,6,7,8\) ta sẽ được các hợp số: \(20; 21; 22; 24; 25; 26; 27; 28.\)
Lần lượt thay \(*\) thành \(0,2,3,4,5,6,8,9\) ta sẽ được các hợp số: \(30; 32; 33; 34; 35; 36; 38; 39.\)
b)
Lần lượt thay \(*\) thành \(1,3,7,9\) ta sẽ được các số nguyên tố: \(11;13;17;19.\)
Lần lượt thay \(*\) thành \(1,3,7\) ta sẽ được các số nguyên tố: \(41;43;47.\)
\(\)
\(4\).
a) Điền “Đ” (đúng), “S”(sai) vào các ô trống cho mỗi kết luận trong bảng sau:

b) Với mỗi kết luận sai trong câu a, hãy cho ví dụ minh hoạ.
Giải
a)
i, ii, iv đúng; iii sai.
b)
Ta có \(14+9=23\) nên iii sai.
\(\)
\(5\).
a) Viết mỗi số sau thành tổng của hai số nguyên tố: \(16; 18; 20.\)
b) Viết \(15\) thành tổng của \(3\) số nguyên tố.
Giải
Tra bảng nguyên tố ta được:
a)
\(16 = 3 + 13 = 5 + 11;\)
\(18 = 5 + 13 = 7 + 11 ;\)
\(20 = 3 + 17 = 7 + 13.\)
b)
\(15 = 3 + 5 + 7.\)
\(\)
Xem bài giải trước: Bài 9. Ước và bội
Xem bài giải tiếp theo: Bài 10. Số nguyên tố. Hợp số. Phân tích một số ra thừa số nguyên tố (Phần 2: Bài 6 đến Bài 10)
Xem các bài giải khác: Giải bài tập Toán Lớp 6 – NXB Chân Trời Sáng Tạo

Đường tuy ngắn không đi không đến; Việc tuy nhỏ không làm không nên.