Bài tập cuối chương \(4\) (Phần \(2\): bài \(8\) đến bài \(14\)) trang \(88\) Vở bài tập toán lớp \(7\) tập \(1\) NXB Chân Trời Sáng Tạo.
\(8.\) Quan sát Hình \(5\), hãy chứng tỏ rằng xy // zt.
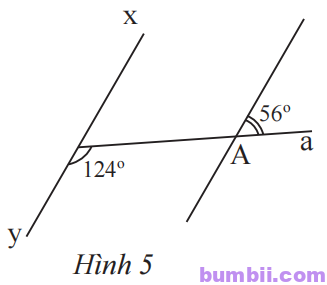
Giải
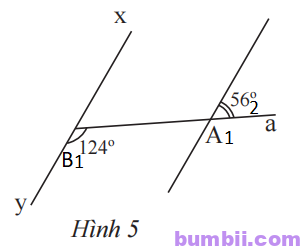
Đặt các góc \(\widehat{A_1} , \widehat{A_2}\) và \(\widehat{B_1}\) như hình vẽ.
Ta có \(\widehat{A_1}\) và \(\widehat{A_2}\) là hai góc kề bù nên:
\(\widehat{A_1} + \widehat{A_2} = 180^o\)
Suy ra \(\widehat{A_1} = 180^o – \widehat{A_2} = 180^o – 56^o = 124^o\)
Do \(\widehat{A_1} = \widehat{B_1} = 124^o\)
Mà \(\widehat{A_1}\) và \(\widehat{B_1}\) ở vị trí đồng vị
Nên xy//zt.
\(\)
\(9.\) Quan sát Hình \(6\), hãy chứng tỏ rằng MN // EF.
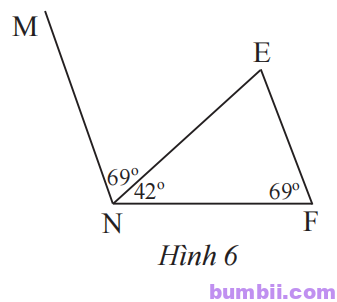
Giải
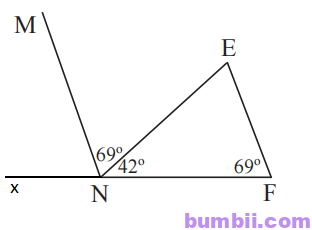
\(\widehat{MNE} + \widehat{ENF} = \widehat{MNF}\) (hai góc kề nhau)
Suy ra \(\widehat{MNF} = 69^o + 42^o = 111^o.\)
Vẽ tia Ox là tia đối của NF.
Khi đó \(\widehat{xNM}\) và \(\widehat{MNF}\) là hai góc kề bù nên:
\(\widehat{xNM} + \widehat{MNF} = 180^o\)
Suy ra \(\widehat{xNM} = 180^o – \widehat{MNF} = 180^o – 111^o = 69^o\)
Do \(\widehat{xNM} = \widehat{NFE} = 69^o\).
Mà \(\widehat{xNM}\) và \(\widehat{NFE}\) ở vị trí đồng vị
Suy ta MN//EF.
\(\)
\(10.\) Quan sát Hình \(7.\)
a) Chứng minh rằng MN // RS.
b) Cho \(\widehat{O_1} =142^o\). Tính \(\widehat{N_1},\ \widehat{S_1}.\)
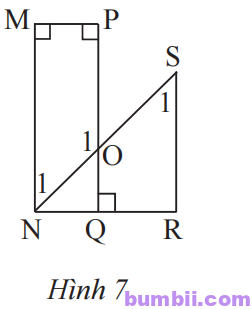
Giải
a) Ta có MN // PQ (vì cùng vuông góc với MP).
Ta lại có PQ // RS (vì cùng vuông góc với QR).
Suy ra MN // RS.
b) \(\widehat{QOS} + \widehat{S_1} = 180^o\)
Suy ra \(\widehat{S_1} = 180^o – \widehat{QOS} = 180^o – 142^o = 38^o\).
Vì MN // RS nên ta có:
\(\widehat{N_1} = \widehat{S_1} = 38^o\) (hai góc so le trong).
\(\)
\(11.\) Quan sát Hình \(8\).
a) Chứng minh rằng m // n.
b) Cho \(\widehat{N_2} =142^o\). Tính \(\widehat{M_1},\ \widehat{M_2}.\)
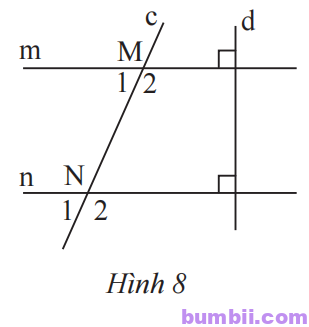
Giải
a) Ta có m \(⊥\) d và n \(⊥\) d.
Do đó m // n (hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song).
Vậy m // n.
b) Vì m // n nên \(\widehat{M_2} = \widehat{N_2} = 70^o\) (hai góc đồng vị.)
Mà \(\widehat{M_1}\) và \(\widehat{M_2}\) là hai góc kề bù nên:
\(\widehat{M_1} + \widehat{M_2} = 180^o\).
Suy ra \(\widehat{M_1} = 180^o – \widehat{M_2} = 180^o – 70^o = 110^o\).
Vậy \(\widehat{M_2} = 70^o\) và \(\widehat{M_1} = 110^o\).
\(\)
\(12.\) Hãy phát biểu phần kết luận còn thiếu của định lí sau:
a) Nếu một đường thẳng cắt hai đường thẳng song song thì tạo thành các cặp góc đồng vị .?.
b) Nếu hai đường thẳng cùng tạo với một đường thẳng các góc so le trong bằng nhau thì .?.
Giải
a) Nếu một đường thẳng cắt hai đường thẳng song song thì tạo thành các cặp góc đồng vị bằng nhau.
b) Nếu hai đường thẳng cùng tạo với một đường thẳng các góc so le trong bằng nhau thì hai đường thẳng đó song song với nhau.
\(\)
\(13.\) Hãy phát biểu phần kết luận còn thiếu của định lí sau:
a) Hai góc cùng bù một góc thứ ba thì .?.
b) Hai đường phân giác của hai góc kề bù thì .?.
Giải
a) Hai góc cùng bù một góc thứ ba thì bằng nhau.
b) Hai đường phân giác của hai góc kề bù thì vuông góc.
\(\)
\(14.\) Cho định lí: “Nếu một đường thẳng cắt hai đường thẳng sao cho có một cặp góc so le trong bằng nhau thì các cặp góc đồng vị có được cũng bằng nhau”.
a) Hãy vẽ hình minh họa định lí trên.
b) Viết giả thiết và kết luận của định lí.
c) Hãy chứng minh định lí trên.
Giải
a) Hình minh họa:
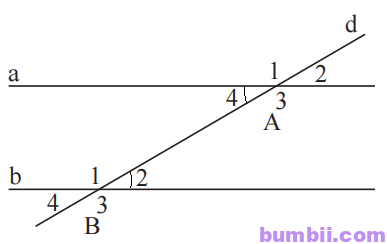
b) Viết giả thiết và kết luận:
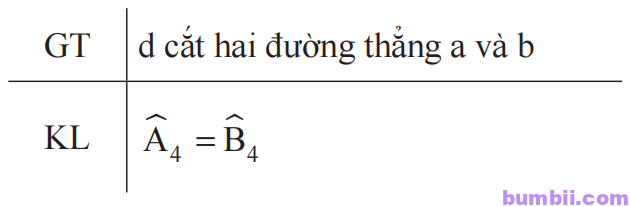
c) Chứng minh định lí trên
Ta có \(\widehat{B_4} = \widehat{B_2}\) (góc đối đỉnh) và \(\widehat{A_4} = \widehat{B_2}\) (giả thiết) suy ra \(\widehat{A_4} = \widehat{B_4}\).
\(\)
Xem bài giải trước: Bài 4: Định lí và chứng minh một định lí
Xem bài giải tiếp theo: Bài 1: Thu thập và phân loại dữ liệu
Xem thêm các bài giải khác tại: Giải Bài tập Toán Lớp 7 – NXB Chân Trời Sáng Tạo
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech
