Chương 8 – Bài 3: Tam giác cân trang 49 sách bài tập toán lớp 7 tập 2 NXB Chân Trời Sáng Tạo.
\(1.\) Cho tam giác MNP cân tại M. Kể tên các cạnh bên, cạnh đáy, góc ở đỉnh, góc ở đáy của tam giác cân đó.
Giải
Tam giác MNP cân tại M có: các cạnh bên là MN và MP, cạnh đáy là NP, góc ở đỉnh là \(\widehat{M}\), góc ở đáy là \(\widehat{N}\) và \(\widehat{P}\).
\(\)
\(2.\) a) Tam giác có hai góc bằng \(60^o\) có phải là tam giác cân hay không? Hãy tìm góc còn lại của tam giác này.
b) Tam giác có hai góc bằng \(45^o\) có phải tam giác cân hay không? Hãy tìm góc còn lại của tam giác này.
Giải
a) Tam giác có hai góc bằng \(60^o\) thì góc còn lại bằng \(180^o\ -60^o\ -60^o=60^o\). Tam giác này vừa là tam giác đều vừa là tam giác cân tại ba đỉnh.
b) Tam giác có hai góc bằng \(45^o\) thì góc còn lại bằng \(180^o\ -45^o\ -45^o=90^o\). Tam giác này vừa là tam giác cân vừa là tam giác vuông và gọi tắt là tam giác vuông cân.
\(\)
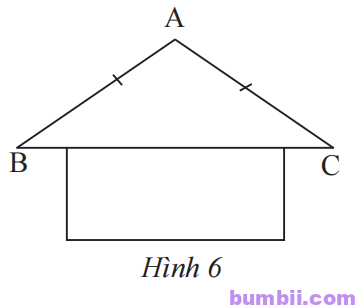
\(3.\) Trong Hình 6, tính góc B và góc C biết \(\widehat{A} = 138^o\).
Giải
Ta có: AB = AC nên \(\Delta ABC\) cân tại A suy ra \(\widehat{B} =\widehat{C} =\displaystyle\frac{180^o-138^o}{2}=21^o.\)
\(\)
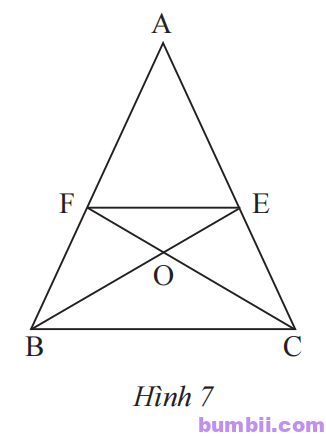
\(4.\) Cho Hình 7, biết AB = AC và BE là tia phân giác của \(\widehat{ABC}\); CF là tia phân giác của \(\widehat{ACB}\). Chứng minh rằng:
a) \(\Delta ABE=\Delta ΔACF;\)
b) Tam giác OEF cân.
Giải
a) Ta có AB = AC nên \(\Delta ABC\) cân tại A suy ra \(\widehat{ABC} = \widehat{ACB}\).
BE là tia phân giác của \(\widehat{ABC}\); CF là tia phân giác của \(\widehat{ACB}\)
Do đó \(\widehat{FCA} = \widehat{EBA}.\)
Xét \(\Delta ACF\) và \(\Delta ABE\) ta có:
AB = AC (giả thiết)
\(\widehat{A}\) là góc chung
\(\widehat{FCA} = \widehat{EBA}\) (chứng minh trên)
Vậy \(\Delta ACF=\Delta ABE\) (g.c.g).
b) Ta có \(\Delta ABE=\Delta ACF\), suy ra BE = CF (1).
Ta lại có \(\widehat{OBC}=\widehat{OCB}\) nên tam giác OBC cân tại O, suy ra OB = OC (2)
Từ (1) và (2) suy ra OE = OF.
Vậy tam giác OEF cân tại O.
\(\)
\(5.\) Cho tam giác MEF cân tại M có \(\widehat{M} =80^o.\)
a) Tính \(\widehat{E},\ \widehat{F}\)
b) Gọi N, P lần lượt là trung điểm của ME, MF. Chứng minh rằng tam giác MNP cân.
c) Chứng minh rằng NP//EF.
Giải
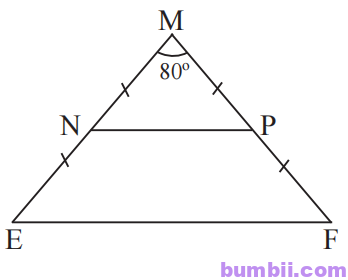
a) Ta có tam giác MEF cân tại M nên: \(\widehat{E} = \widehat{F} =\displaystyle\frac{180^o-80^o}{2}=50^o.\)
b) \(\Delta MEF\) cân tại M, do đó ME = MF.
Mà N, P lần lượt là trung điểm của ME, MF.
Suy ra \(MN=\displaystyle\frac{ME}{2}=\displaystyle\frac{MF}{2}=MP.\)
Vậy tam giác MNP cân tại M.
c) Trong tam giác cân MEF, ta có \(\widehat{N} =\widehat{P} =\displaystyle\frac{180^o-80^o}{2}=50^o\)
Ta lại có \(\widehat{MNP} =\widehat{NEF} =50^o\), suy ra NP//EF (vì có hai góc đồng vị bằng nhau)
\(\)
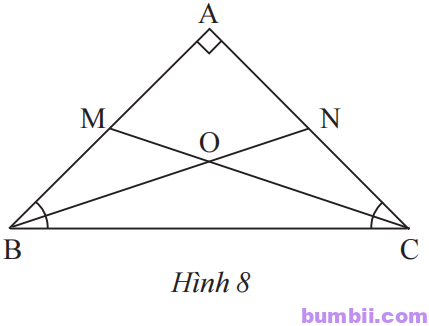
\(6.\) Cho tam giác ABC vuông cân tại A. Tia phân giác của góc B cắt AC tại N, tia phân giác của góc C cắt AB tại M. Gọi O là giao điểm của BN và CM.
a) Tính số đo các góc OBC, OCB.
b) Chứng minh rằng tam giác OBC cân.
c) Tính số đo góc BOC.
Giải
a) Ta có \(\widehat{ABC} =\widehat{ACB}\) (tam giác ABC vuông cân tại A).
BO là tia phân giác \(\widehat{ABC}\), CO là tia phân giác \(\widehat{ACB}.\)
Do đó \(\widehat{OBC} =\widehat{OCB} =\displaystyle\frac{180^o-90^o}{2}=22,5^o.\)
b) Tam giác OBC có \(\widehat{OBC} =\widehat{OCB}\) nên là tam giác cân tại O.
c) Ta có \(\widehat{BOC} = 180^o – \widehat{OBC}\ – \widehat{OCB}\)
\(=180^o-22,5^o-22,5^o=135^o.\)
\(\)
Xem bài giải trước: Bài 2: Tam giác bằng nhau
Xem bài giải tiếp theo: Bài 4: Đường vuông góc và đường xiên
Xem thêm các bài giải khác tại: Giải Bài tập Toán Lớp 7 – NXB Chân Trời Sáng Tạo
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech
