Bài 2. Tính chất cơ bản của phân số trang 11 Vở bài tập toán lớp 6 tập 2 NXB Chân Trời Sáng Tạo
\(1\). Quy đồng mẫu số các phân số sau:
a) \(\displaystyle \frac{11}{-12} \text{ và } \displaystyle \frac{-17}{18};\)
b) \(\displaystyle \frac{-9}{15} \text{ và } \displaystyle \frac{17}{-20};\)
c) \(\displaystyle \frac{-5}{6}; \displaystyle \frac{-2}{5} \text{ và } \displaystyle \frac{7}{-12}.\)
Giải
a)
Vì \(BCNN(12,18)=36\) nên ta chọn mẫu số chung là \(36.\)
\(\displaystyle \frac{11}{-12}=\displaystyle \frac{-11.3}{12.3}=\displaystyle \frac{-33}{36}.\)
\(\displaystyle \frac{-17}{18}=\displaystyle \frac{-17.2}{18.2}=\displaystyle \frac{-34}{36}.\)
b)
Vì \(BCNN(15,20)=60\) nên ta chọn mẫu số chung là \(60.\)
\(\displaystyle \frac{-9}{15}=\displaystyle \frac{-9.4}{15.4}=\displaystyle \frac{-36}{60}.\)
\(\displaystyle \frac{17}{-20}=\displaystyle \frac{-17.3}{20.3}=\displaystyle \frac{-51}{60}.\)
c)
Vì \(BCNN(6,5,12)=60\) nên ta chọn mẫu số chung là \(60.\)
\(\displaystyle \frac{-5}{6}=\displaystyle \frac{-5.10}{6.10}=\displaystyle \frac{-50}{60}.\)
\(\displaystyle \frac{-2}{5}=\displaystyle \frac{-2.12}{5.12}=\displaystyle \frac{-24}{60}.\)
\(\displaystyle \frac{7}{-12}=\displaystyle \frac{-7.5}{12.5}=\displaystyle \frac{-35}{60}.\)
\(\)
\(2\). Viết các số sau thành các phân số có cùng mẫu số (chọn mẫu số chung là số dương nhỏ nhất nếu được)
a) \(-5;\displaystyle \frac{17}{-20} \text{ và } \displaystyle \frac{-16}{9};\)
b) \(\displaystyle \frac{13}{-15}; \displaystyle \frac{-18}{25} \text{ và } -3.\)
Giải
a)
Vì \(BCNN(20,9)=180\) nên ta chọn mẫu số chung là \(180.\)
\(-5=\displaystyle \frac{-5.180}{1.180}=\displaystyle \frac{-900}{180}.\)
\(\displaystyle \frac{17}{-20}=\displaystyle \frac{-17.9}{20.9}=\displaystyle \frac{-153}{180}.\)
\(\displaystyle \frac{-16}{9}=\displaystyle \frac{-16.20}{9.20}=\displaystyle \frac{-320}{180}.\)
b)
Vì \(BCNN(15,25)=75\) nên ta chọn mẫu số chung là \(75.\)
\(\displaystyle \frac{13}{-15}=\displaystyle \frac{-13.5}{15.5}=\displaystyle \frac{-65}{75}.\)
\(\displaystyle \frac{-18}{25}=\displaystyle \frac{-18.3}{25.3}=\displaystyle \frac{-54}{75}.\)
\(-3=\displaystyle \frac{-3.75}{1.75}=\displaystyle \frac{-225}{75}.\)
\(\)
\(3\). Rút gọn các phân số sau:
a) \(\displaystyle \frac{390}{-240};\)
b) \(\displaystyle \frac{-60}{84};\)
c) \(\displaystyle \frac{6262}{-6666};\)
d) \(\displaystyle \frac{-2020}{2024}.\)
Giải
a)
\(\displaystyle \frac{390}{-240}=\displaystyle \frac{39}{-24}=\displaystyle \frac{13}{-8}.\)
b)
\(\displaystyle \frac{-60}{84}=\displaystyle \frac{-10}{14}=\displaystyle \frac{-5}{7}.\)
c)
\(\displaystyle \frac{6262}{-6666}=\displaystyle \frac{3131}{-3333}=\displaystyle \frac{3131:101}{-3333:101}=\displaystyle \frac{31}{-33}.\)
d)
\(\displaystyle \frac{-2020}{2024}=\displaystyle \frac{-2020:4}{2024:4}=\displaystyle \frac{-505}{506}.\)
\(\)
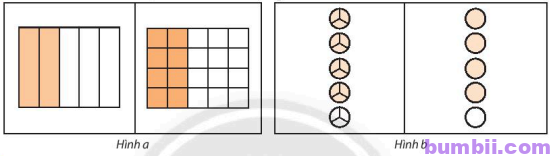
\(4\). Hình vẽ sau minh hoạ tính chất nào của phân số?
Giải
Hình a) minh họa tính chất \(1\) (Quy đồng) của phân số: \(\displaystyle \frac{2}{5}=\displaystyle \frac{2.4}{5.4}=\displaystyle \frac{8}{20}.\)
Hình b) minh họa tính chất \(2\) (Rút gọn) của phân số: \(\displaystyle \frac{12}{15}=\displaystyle \frac{12:3}{15:3}=\displaystyle \frac{4}{5}.\)
\(\)
\(5\). Nêu hai cách giải thích các phân số sau bằng nhau (dùng khái niệm bằng nhau và dùng tính chất)
a) \(\displaystyle \frac{-15}{33} \text{ và } \displaystyle \frac{5}{-11};\)
b) \(\displaystyle \frac{7}{-12} \text{ và } \displaystyle \frac{35}{-60};\)
c) \(\displaystyle \frac{-8}{14} \text{ và } \displaystyle \frac{12}{-21}.\)
Giải
a)
Ta có \(\displaystyle \frac{-15}{33} = \displaystyle \frac{5}{-11}\) vì:
Cách 1: \((-15).(-11)=5.33.\)
Cách 2: \(\displaystyle \frac{-15}{33} = \displaystyle \frac{-15:(-3)}{33:(-3)} = \displaystyle \frac{5}{-11}.\)
b)
Ta có \(\displaystyle \frac{7}{-12} = \displaystyle \frac{35}{-60}\) vì:
Cách 1: \(7.(-60)=35.(-12).\)
Cách 2: \(\displaystyle \frac{7}{-12} = \displaystyle \frac{7.5}{(-12).5} = \displaystyle \frac{35}{-60}\)
c)
Ta có \(\displaystyle \frac{-8}{14}=\displaystyle \frac{12}{-21}\) vì:
Cách 1:
\((-8).(-21)=12.14.\)
Cách 2:
\(\displaystyle \frac{-8}{14}=\displaystyle \frac{-8.3}{14.3}=\displaystyle \frac{-24}{42}.\)
\(\displaystyle \frac{12}{-21}=\displaystyle \frac{12.(-2)}{-21.(-2)}=\displaystyle \frac{-24}{42}.\)
\(\)
\(6\). Dùng phân số để viết các đại lượng khối lượng sau theo tạ, theo tấn.
a) \(223 \) kg;
b) \(18 \) kg;
c) \(2020 \) kg;
d) \(7 \) kg.
Giải
a) \(223\) kg \(= \displaystyle \frac{223}{100}\) tạ \(= \displaystyle \frac{223}{1000}\) tấn.
b) \(18\) kg \(= \displaystyle \frac{18}{100}\) tạ \(= \displaystyle \frac{9}{50}\) tạ = \(\displaystyle \frac{9}{500}\) tấn.
c) \(2020\) kg \(= \displaystyle \frac{2020}{100}\) tạ \(= \displaystyle \frac{101}{5}\) tạ = \(\displaystyle \frac{101}{50}\) tấn.
d) \(7\) kg \(= \displaystyle \frac{7}{100}\) tạ \(= \displaystyle \frac{7}{1000}\) tấn.
\(\)
\(7\). Dùng phân số với mẫu số dương nhỏ nhất để viết các đại lượng dung tích sau theo lít.
a) \(600 \) ml;
b) \(280 \) ml;
c) \(1300 \) ml;
d) \(970 \) ml.
Giải
a) \(600\) ml \(= \displaystyle \frac{600}{1000}\) l = \(\displaystyle \frac{6}{10}\) l = \(\displaystyle \frac{3}{5}\) l.
b) \(280\) ml \(= \displaystyle \frac{280}{1000}\) l = \(\displaystyle \frac{28}{100}\) l = \(\displaystyle \frac{7}{25}\) l.
c) \(1300\) ml \(= \displaystyle \frac{1300}{1000}\) l = \(\displaystyle \frac{13}{10}\) l.
d) \(970\) ml \(= \displaystyle \frac{970}{1000}\) l = \(\displaystyle \frac{97}{100}\) l.
\(\)
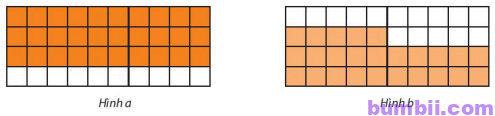
\(8\). Dùng phân số với mẫu số dương nhỏ nhất để biểu thị phần tô màu trong mỗi hình vẽ sau:
Giải
a)
Phân số biểu thị phần tô màu là \(\displaystyle \frac{30}{40} = \displaystyle \frac{3}{4}.\)
b)
Phân số biểu thị phần tô màu là \(\displaystyle \frac{25}{40} = \displaystyle \frac{5}{8}.\)
\(\)
Xem bài giải trước: Bài 1. Phân số với tử số và mẫu số là số nguyên
Xem bài giải tiếp theo: Bài 3. So sánh phân số
Xem các bài giải khác: Giải bài tập Toán Lớp 6 – NXB Chân Trời Sáng Tạo

Đường tuy ngắn không đi không đến; Việc tuy nhỏ không làm không nên.