Bài tập cuối chương I

Chương \(I\) – Bài tập cuối chương trang \(27\) SGK Toán Lớp \(10\) Tập \(1\) NXB Chân trời sáng tạo. Các em hãy cùng Bumbii giải các bài tập sau.

Bài \(1\). Xét tính đúng sai của mỗi mệnh đề sau:

\(a) \{a\} \in \{ a; b; c; d \}\);

\(b) \emptyset = \{ 0 \}\);

\(c) \{ a; b; c; d = \{ b; a; d; c \}\);

\(a) \{ a; b; c\} \not\subset \{ a; b; c \}\).

Trả lời:

\(a)\) Mệnh đề \(a)\) sai vì:

\(\{a\}, \{a; b; c; d\}\) là kí hiệu của tập hợp nên không dùng \(\in\) mà cần dùng kí hiệu \(\subset\) như sau:

\(\{a\} \subset \{a; b; v; d\} \).

\(b)\) Mệnh đề \(b)\) sai vì \(\emptyset\) là tập hợp không có phần tử nào, \(\{0\}\) là tập hợp chứa \(1\) phần tử là \(0\).

\(c)\) Ta có: \(\{a; b; c; d\} = \{ b; a; d; c\}\) nên mệnh đề \(c)\) đúng.

\(d)\) Vì mỗi tập hợp là tập con của chính nó nên \(\{ a; b; c \} \subset \{a; b; c\}\).

Vậy mệnh đề \(d)\) là mệnh đề sai.

\(\)

Bài \(2\). Xét tính đúng sai của mỗi mệnh đề sau:

\(a)\) Nếu \(2a \ – \ 1 > 0 \) thì \(a > 0\) (\(a\) là số thực cho trước).

\(b) a \ – \ 2 > b\) nếu và chỉ nếu \( a > b + 2 \) (\(a, b\) là hai số thực cho trước).

Trả lời:

\(a)\) Ta có: \( 2a \ – \ 1 > 0 \Leftrightarrow 2a > 1 \Leftrightarrow a > \displaystyle\frac{1}{2} > 0\)

\(\Leftrightarrow a > 0\)

Do đó mệnh đề \(a)\) đúng.

\(b)\) Với \(a, b\) là hai số thực cho trước ta có:

\( a \ – \ 2 > b \Leftrightarrow a \ – \ 2 + 2 > b + 2\) (Liên hệ giữa thứ tự và phép cộng).

\(\Leftrightarrow a > b + 2\)

Vì vậy mệnh đề \(b)\) đúng.

\(\)

Bài \(3\). Sử dụng thuật ngữ “điều kiện cần”, “điều kiện đủ”, phát biểu lại các định lí sau:

\(a)\) Nếu \(B \subset A\) thì \( A \cup B = A\) ( \(A, B \) là hai tập hợp);

\(b)\) Một hình bình hành \( ABCD\) có hai đường chéo vuông góc với nhau thì nó là hình thoi.

Trả lời:

Sử dụng thuật ngữ “điều kiện cần”, “điều kiện đủ” ta phát biểu lại các định lý như sau:

\(a)\) \(B \subset A\) là điều kiện đủ để có \(A \cup B = A\).

\(A \cup B = A\) là điều kiện cần để có \(B \subset A\).

\(b)\) Một hình bình hành \(ABCD\) có hai đường chéo vuông góc với nhau là điều kiện đủ để nó là hình thoi.

Hình bình hành \(ABCD\) là hình thoi là điều kiện cần để hai đường chéo của nó vuông góc với nhau.

\(\)

Bài \(4\). Cho định lí:

\(” \forall x \in \mathbb{R}, x \in \mathbb{Z}\) nếu và chỉ nếu \( x + 1 \in \mathbb{Z}”\).

Phát biểu lại định lí này , sử dụng thuật ngữ “điều kiện cần và đủ”.

Trả lời:

Sử dụng thuật ngữ “điều kiện và đủ”, định lý được phát biểu lại như sau:

\( \forall x \in \mathbb{R}\), điều kiện cần và đủ để \( x \in \mathbb{Z}\) là \( x + 1 \in \mathbb{Z}\).

\(\)

Bài \(5\). Xét tính đúng sai của các mệnh đề sau:

\(a) \forall x \in \mathbb{N}, x^3 > x \);

\(b) \exists x \in \mathbb{Z}, x \notin \mathbb{N}\);

\(c) \forall x \in \mathbb{R}\), nếu \( x \in \mathbb{Z}\) thì \( x \in \mathbb{Q}\).

Trả lời:

\(a)\) Xét với \(x = 0 \in \mathbb{N}\) ta có:

\( x ^ 3 = 1^ 3= 1 = x \Rightarrow \exists\) giá trị \(x\) không thoả mãn \( x ^ 3 > x\)

Do đó mệnh đề \(a\) là mệnh đề sai.

\(b)\) Xét với \( x = \ – \ 1\)

Ta có \( \ – \ 1 \in \mathbb{Z}, \ – \ 1 \notin \mathbb{N}\).

Do đó mệnh đề \(b\) là mệnh đề đúng.

\(c)\) Ta có \( \mathbb{Z} \subset \mathbb{Q}\) nên mệnh đề \(c\) là mệnh đề đúng.

\(\)

Bài \(6\). Xét quan hệ bao hàm giữa các tập hợp dưới đây. Vẽ biểu đồ Ven để thể hiện các quan hệ bao hàm đó.

\(A\) là tập hợp các hình tứ giác;

\(B\) là tập hợp các hình bình hành;

\(C\) là tập hợp các hình chữ nhật;

\(D\) là tập hợp các hình vuông;

\(E\) là tập hợp các hình thoi.

Trả lời: Ta có:

• Hình bình hành là tứ giác có một cặp cạnh đối song song và bằng nhau \(\Rightarrow B \subset A\)

• Hình chữ nhật là hình bình hành có một góc vuông \(\Rightarrow C \subset B\)

• Hình vuông là hình chữ nhật có hai cạnh kề bằng nhau \(\Rightarrow D \subset C\)

• Hình vuông là hình thoi có một góc vuông \(\Rightarrow D \subset E\)

• Hình thoi là hình bình hành có hai cạnh kề bằng nhau \(\Rightarrow E \subset B\)

Tập hợp các hình vừa là hình chữ nhật vừa là hình thoi (hình chữ nhật có bốn cạnh bằng nhau) là các hình vuông \( \Leftrightarrow D = C \cap E\)

Kết hợp lại, ta có:

\( \left \{\begin{matrix} D \subset C \subset B \subset A\\ D \subset E \subset B \subset A\\ C \cap E = D \end{matrix} \right.\).

Ta vẽ được biểu đồ Ven sau:

\(\)

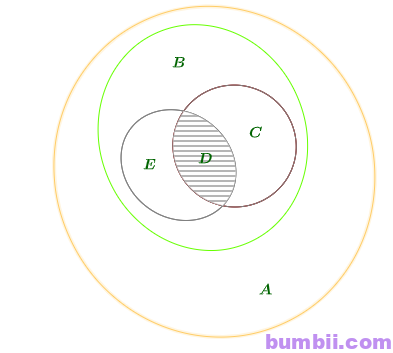
Bài \(7. a)\) Hãy viết tất cả các tập con của tập hợp \(A = \{a; b; c\}\).

\(b)\) Tìm tất cả các tập hợp \(B\) thoả mãn điều kiện \(\{a; b\} \subset B \subset \{a; b; c; d\}\).

Trả lời:

\(a)\) Các tập con của tập \(A\) gồm:

• Tập không có phần tử nào: \(\emptyset\);

• Tập có một phần tử: \(\{a\}; \{b\}; \{c\}\);

• Tập có hai phần tử: \(\{a; b\}; \{a; c\}; \{b; c\}\);

• Tập có ba phần tử: \(\{a; b; c\}\)

Vậy các tập hợp con của tập \(A\) gồm: \(\{\emptyset\}; \{a\}; \{b\}; \{c\}; \{a; b\}; \{a; c\}; \{b; c\}; \{a;b;c\}\).

\(b)\) Các tập hợp \(B\) thoả mãn điều kiện \(\{a; b\} \subset B \subset \{a; b; c; d\}\) là:

\(B = \{a; b; c; d\}; \{a; b; c\}; \{ a; b; d\}; \{a; b\}\).

Vậy \(B = \{a; b; c; d\}; \{a; b; c\}; \{ a; b; d\}; \{a; b\}\).

\(\)

Bài \(8\). Cho \(A = \{ x \in \mathbb{R} \ | \ x^2 \ – \ 5x \ – \ 6 = 0\}\),

\(B = \{x \in \mathbb{R} \ | \ x^2 = 1\}\).

Tìm \( A \cap B, A \cup B, A \setminus B, B \setminus A\).

Trả lời: Ta có:

• \(x^2 \ – \ 5x \ – \ 6 = 0 \Leftrightarrow (x + 1 )(x \ – \ 6) = 0\)

\(\Leftrightarrow \left [ \begin{matrix} x = \ – \ 1\\ x = 6 \end{matrix} \right.\)

\(\Rightarrow A = \{\ – \ 1; 6\}\).

• \( x ^ 2 = 1 \Leftrightarrow \left [ \begin{matrix} x = 1\\ x = \ – \ 1 \end{matrix} \right.\)

\(\Rightarrow B = \{ \ – \ 1; 1\}\)

Từ đó suy ra: \( A \cap B = \{ \ – \ 1\}\)

\( A \cup B = \{ \ – \ 1; 1; 6\}\)

\( A \setminus B = \{6\}; B \setminus A = \{1\}\).

\(\)

Bài \(9\). Cho \(A = \{ x \in \mathbb{R} \ | \ 1 \ – \ 2x \leq 0\}\),

\(B = \{ x \in \mathbb{R} \ | \ x \ – \ 2 < 0\}\).

Tìm \( A \cap B, A \cup B\).

Trả lời: Ta có:

• \( 1 \ – \ 2x \leq 0 \Leftrightarrow 2x \geq 1\)

\(\Leftrightarrow x \geq \displaystyle \frac{1}{2}\)

Suy ra \(A = [\displaystyle \frac{1}{2}; +\infty)\)

• \( x \ – 2 < 0 \Leftrightarrow x < 2\)

Suy ra \(B= ( \ – \ \infty; 2)\)

Để xác định \(A \cap B\) ta có sơ đồ sau:

Suy ra \(A \cap B = [ \displaystyle \frac{1}{2}; 2)\).

Để xác định \(A \cup B\) ta có sơ đồ sau:

Suy ra \(A \cup B = ( \ – \ \infty; + \infty )\)

Vậy \( A \cap B = [ \displaystyle \frac{1}{2}; 2); A \cup B = ( \ – \ \infty; + \infty )\).

\(\)

Bài \(10\). Lớp \(10C\) có \(45\) học sinh, trong đó có \(18\) học sinh tham gia cuộc thi vẽ đồ hoạ trên máy tính, \(24\) học sinh tham gia cuộc thi tin học văn phòng cấp trường và \(9\) học sinh không tham gia cả hai cuộc thi này. Hỏi có bao nhiêu học sinh của lớp \(10C\) tham gia đồng thời hai cuộc thi?

Trả lời:

Gọi A là tập hợp số học sinh lớp \(10C\) tham gia cuộc thi vẽ đồ hoạ trên máy tính, B là tập hợp số học sinh lớp \(10C\) tham gia cuộc thi tin học văn phòng cấp trường.

\(Rightarrow\) Số học sinh tham gia ít nhất một cuộc thi vẽ đồ hoạ trên máy tính hoặc cuộc thi tin học văn phòng cấp trường là: \( 45 \ – \ 9 = 36\) (học sinh)

\(\Rightarrow n ( A \cup B) = 36\)

Ta lại có: \( n (A) = 18; n (B) = 24\)

\(\Rightarrow\) Số học sinh tham gia đồng thời cả hai cuộc thi là:

\( n ( A \cap B = n (A) + n (B) \ – \ n ( A \cup B ) = 18 + 24 \ – \ 36 = 6\) (học sinh).

Vậy lớp \(10C\) có \(6\) học sinh tham gia đồng thời hai cuộc thi.

Bài tập cuối chương I

Xem bài giải trước: https://bumbii.com/bai-3-cac-phep-toan-tren-tap-hop/
Xem bài giải tiếp theo: https://bumbii.com/bai-1-bat-phuong-trinh-bac-nhat-hai-an/
Xem các bài giải khác: https://bumbii.com/giai-toan-lop-10-nxb-chan-troi-sang-tao

Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech