Bài tập cuối chương 2 trang 47 sách giáo khoa toán lớp 8 tập 1 NXB Kết nối tri thức với cuộc sống. Các em cùng Bumbii giải các bài tập sau.
A. TRẮC NGHIỆM
Chọn phương án đúng trong mỗi câu sau:
2.28. Đa thức \(x^2-9x+8\) được phân tích thành tích của hai đa thức
A. \(x-1\) và \(x + 8.\)
B. \(x-1\) và \(x-8.\)
C. \(x-2\) và \(x-4.\)
D. \(x-2\) và \(x + 4.\)
Giải
\(x^2-9x+8= (x^2-x)-(8x-8)\)
\(= x(x-1)-8(x-1) = (x-1)(x-8).\)
Chọn đáp án B.
\(\)
2.29. Khẳng định nào sau đây là đúng?
A. \((A-B)(A+B)=A^2+2AB+B^2.\)
B. \((A+B)(A-B)=A^2-2AB+B^2.\)
C. \((A+B)(A-B)=A^2+B^2.\)
D. \((A+B)(A-B)=A^2-B^2.\)
Giải
Chọn đáp án D.
\(\)
2.30. Biểu thức \(25x^2+20xy+4y^2\) viết dưới dạng bình phương của một tổng là:
A. \([5x+(-2y)]^2.\)
B. \([2x+(-5y)]^2.\)
C. \((2x+5y)^2.\)
D. \((5x+2y)^2.\)
Giải
\(25x^2+20xy+4y^2=(5x+2y)^2.\)
Chọn đáp án D.
\(\)
2.31. Rút gọn biểu thức \(A=(2x+1)^3-6x(2x+1)\) ta được
A. \(x^3+8.\)
B. \(x^3+1.\)
C. \(8x^3+1.\)
D. \(8x^3-1.\)
Giải
\(A=(2x+1)^3-6x(2x+1)\)
\(= (2x)^3 + 3 . (2x)^2 . 1 + 3 . 2x . 1^2 + 1^3-12x^2-6x\)
\(= 8x^3 + 12x^2 + 6x + 1-12x^2-6x =8x^3+1.\)
Chọn đáp án C.
\(\)
B. TỰ LUẬN
2.32. Tính nhanh giá trị của các biểu thức:
a) \(x^2-4x+4\) tại \(x = 102;\)
b) \(x^3+3x^2+3x+1\) tại \(x = 999.\)
Giải
a) \(x^2-4x + 4 = (x-2)^2\)
Thay \(x = 102\) vào biểu thức \((x-2)2,\) ta có:
\((102-2)^2 = 100^2 = 10 000.\)
b) \(x^3 + 3x^2 + 3x + 1 = (x + 1)^3\)
Thay \(x = 999\) vào biểu thức \((x + 1)^3,\) ta có:
\((999 + 1)^3 = 100^3 = 1 000 000.\)
\(\)
2.33. Rút gọn các biểu thức:
a) \((2x-5y)(2x+5y)+(2x+5y)^2;\)
b) \((x+2y)(x^2-2xy+4y^2)+(2x-y)(4x^2+2xy+y^2).\)
Giải
a) \((2x-5y)(2x+5y)+(2x+5y)^2\)
\(= (2x + 5y)[(2x-5y) + (2x + 5y)]\)
\(= (2x + 5y)4x=8x^2+20xy.\)
b) \((x+2y)(x^2-2xy+4y^2)+(2x-y)(4x^2+2xy+y^2)\)
\(= (x + 2y)[x^2-x . 2y + (2y)^2] + (2x-y)[(2x)^2 + 2x . y + y^2]\)
\(= x^3 + (2y)^3 + x^3-(2y)^3\)
\(= x^3 + x^3 = 2x^3.\)
\(\)
2.34. Phân tích các đa thức sau thành nhân tử:
a) \(6x^2-24y^2;\)
b) \(64x^3-27y^3;\)
c) \(x^4-2x^3+x^2;\)
d) \((x-y)^3+8y^3.\)
Giải
a) \(6x^2-24y^2=6(x^2-4y^2)=6(x-2y)(x+2y).\)
b) \(64x^3-27y^3= (4x)^3-(3y)^3\)
\(=(4x-3y)(16x^2+12xy+9y^2).\)
c) \(x^4-2x^3+x^2=x^2(x^2-2x+1)=x^2(x-1)^2.\)
d) \((x-y)^3+8y^3= (x-y)^3 + (2y)^3\)
\(= (x-y + 2y)[(x-y)^2 + (x-y) . 2y + (2y)^2]\)
\(=(x+y)(x^2-2xy+y^2-2xy+2y^2+4y^2)\)
\(=(x+y)(x^2-4xy+7y^2).\)
\(\)
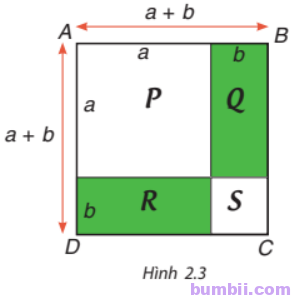
2.35. Sử dụng Hình 2.3. bằng cách tính diện tích hình vuông ABCD theo hai cách, hãy giải thích hằng đẳng thức \((a+b)^2=a^2+2ab+b^2.\)
Giải
Cách 1: Diện tích hình vuông ABCD có độ dài cạnh bằng a + b:
\((a+b)(a+b)=(a+b)^2.\)
Cách 2: Diện tích hình vuông ABCD bằng tổng diện tích các hình P, Q, R, S:
\(P+Q+R+S=a^2+ab+ab+b^2=a^2+2ab+b^2\)
Từ đó, ta có thể giải thích được hằng đẳng thức \((a+b)^2=a^2+2ab+b^2.\)
\(\)
Xem bài giải trước: Luyện tập chung
Xem bài giải tiếp theo: Bài 10. Tứ giác
Xem thêm các bài giải khác tại: Giải bài tập SGK Toán Lớp 8 Kết Nối Tri Thức Với Cuộc Sống
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech
