Chương 2 – Bài 9. Phân tích đa thức thành nhân tử trang 44 sách giáo khoa toán lớp 8 tập 1 NXB Kết nối tri thức với cuộc sống. Các em cùng Bumbii giải các bài tập sau.
2.22. Phân tích các đa thức sau thành nhân tử:
a) \(x^2+xy;\)
b) \(6a^2b-18ab;\)
c) \(x^3-4x;\)
d) \(x^4-8x.\)
Giải
a) \(x^2+xy=x(x+y).\)
b) \(6a^2b-18ab=6ab(a-3).\)
c) \(x^3-4x=x(x^2-4)\) \(=x(x+2)(x-2).\)
d) \(x^4-8x=x(x^3-8)\) \(=x(x-2)(x^2+2x+4).\)
\(\)
2.23. Phân tích các đa thức sau thành nhân tử
a) \(x^2-9+xy+3y;\)
b) \(x^2y+x^2+xy-1.\)
Giải
a) \(x^2-9+xy+3y\)
\(=(x^2-9)+(xy+3y)\)
\(=(x+3)(x-3)+y(x+3)\)
\(=(x+3)(x-3+y).\)
b) \(x^2y+x^2+xy-1\)
\(=(x^2y+xy)+(x^2-1)\)
\(=xy(x+1)+(x-1)(x+1)\)
\(=(x+1)(xy+x-1).\)
\(\)
2.24. Tìm x, biết:
a) \(x^2-4x=0;\)
b) \(2x^3-2x=0.\)
Giải
a) \(x^2-4x=0\)
\(x(x-4)=0\)
\(⇒x=0\) hoặc \(x-4 = 0\)
\(⇒x=0\) hoặc \(x = 4.\)
b) \(2x^3-2x=0\)
\(2x(x-1)=0\)
\(⇒2x=0\) hoặc \(x-1 = 0\)
\(⇒x=0\) hoặc \(x = 1.\)
\(\)
2.25. Một mảnh vườn hình vuông có độ dài cạnh bằng x (mét). Người ta làm đường đi xung quanh mảnh vườn, có độ rộng như nhau và bằng y (mét) (H.2.2)
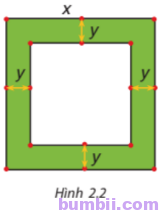
a) Viết biểu thức tính diện tích S của đường bao quanh mảnh vườn theo x và y.
b) Phân tích S thành nhân tử rồi tính S khi x = 102 m, y = 2 m.
Giải
a) Biểu thức tính diện tích S của đường bao quanh mảnh vườn:
\(S=x^2-y^2\ (m^2).\)
b) \(S=x^2-y^2=(x-y)(x+y)\)
Thay \(x = 102\ m,\) \(y = 2\ m\) vào biểu thức S, ta có:
\(S = (102 – 2)(102 + 2)\) \(= 100.104 = 10400\ (m^2).\)
\(\)
Xem bài giải trước: Luyện tập chung
Xem bài giải tiếp theo: Luyện tập chung
Xem thêm các bài giải khác tại: Giải bài tập SGK Toán Lớp 8 Kết Nối Tri Thức Với Cuộc Sống
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech
