Chương 8 – Bài 8: Tính chất ba đường cao của tam giác trang 78 sách giáo khoa toán lớp 7 tập 2 NXB Chân Trời Sáng Tạo.
\(1.\) Cho tam giác ABC vuông tại A. Lấy điểm H thuộc cạnh AB. Vẽ HM vuông góc với BC tại M. Tia MH cắt tia CA tại N. Chứng minh rằng CH vuông góc với NB.
Giải
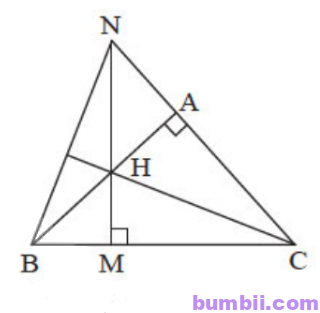
\(\Delta HBN\) có BM và NA là hai đường cao cắt nhau tại C.
Suy ra C là trực tâm của \(\Delta HBN\).
Do đó CH\(\bot\)NB.
\(\)
\(2.\) Cho tam giác ABC vuông tại A. Trên tia BA lấy điểm M sao cho BM = BC. Tia phân giác của góc B cắt AC tại H. Chứng minh rằng MH vuông góc với BC.
Giải
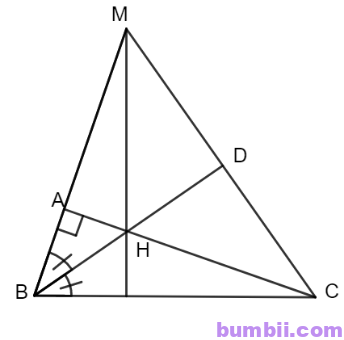
Goi D là giao điểm của BH và MC.
Xét \(\Delta BDM\) và \(\Delta BDC\) có:
\(\widehat{MBD}=\widehat{CBD}\)
BD là cạnh chung
BM = BC
Vậy \(\Delta BDM=\Delta BDC\) (c.g.c)
Suy ra \(\widehat{BDM} = \widehat{BDC} =90^o.\)
CA và BD là hai đường cao của \(\Delta BCM\) cắt nhau tại trực tâm H.
Suy ra MH là đường cao của tam giác BCM.
Vậy MN vuông góc với BC.
\(\)
\(3.\) Cho tam giác ABC vuông cân tại A. Lấy điểm E thuộc cạnh AC. Trên tia đối của tia AB lấy điểm D sao cho AD = AE. Chứng minh rằng:
a) DE vuông góc với BC;
b) BE vuông góc với DC.
Giải
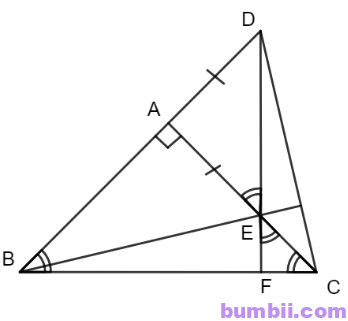
a) DE cắt BC tại F
\(\Delta ABC\) vuông cân tại A suy ra BA\(\bot\)AC hay EA\(\bot\)AD
AD = AE
Suy ra \(\Delta ADE\) vuông cân tại A
=> \(\widehat{AED} = \widehat{ADE} = 45^o\)
\(\widehat{ABC} = \widehat{ACB} = 45^o\) (\(\Delta ABC\) vuông cân tại A)
Xét \(\Delta EFC\) có :
\(\widehat{FEC} + \widehat{FCE} + \widehat{EFC} = 180^o\)
\(45^o + 45^o + \widehat{EFC} = 180^o\)
\(\widehat{EFC} = 180^o – 45^o – 45^o = 90^o\)
Suy ra EF ⊥ BC hay DE ⊥ BC.
\(\)
\(4.\) Cho tam giác nhọn ABC có ba đường cao AD, BE, CF. Biết AD = BE = CF. Chứng minh rằng tam giác ABC đều.
Giải
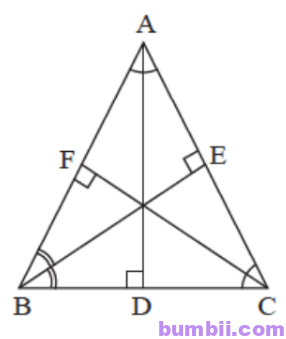
Xét \(\Delta BCF\) vuông tại F và \(\Delta CBE\) vuông tại E có :
BE = CF
BC là cạnh chung
\(\Rightarrow \Delta BCF = \Delta CBE\) (hai tam giác có cạnh huyền và một cạnh góc vuông bằng nhau).
\(\Rightarrow \widehat{CBF} = \widehat{BCE}\).
Xét \(\Delta BAE\) vuông tại E và \(\Delta ABD\) vuông tại D có :
AD = BE
AB là cạnh chung
\(\Rightarrow \Delta BAE = \Delta ABD\) (hai tam giác có cạnh huyền và một cạnh góc vuông bằng nhau).
\(\Rightarrow \widehat{BAE} = \widehat{ABD}\).
Tam giác ABC có ba góc bằng nhau nên là tam giác vuông.
\(\)
Xem bài giải trước: Bài 7: Tính chất ba đường trung tuyến của tam giác
Xem bài giải tiếp theo: Bài 9: Tính chất ba đường phân giác của tam giác
Xem thêm các bài giải khác tại: Giải bài tập SGK Toán Lớp 7 – NXB Chân Trời Sáng Tạo.
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech
