Chương 8 – Bài 6: Tính chất ba đường trung trực của tam giác trang 72 sách giáo khoa toán lớp 7 tập 2 NXB Chân Trời Sáng Tạo.
\(1.\) Vẽ ba tam giác nhọn, vuông, tù.
a) Xác định điểm O cách đều ba đỉnh của mỗi tam giác.
b) Nêu nhận xét của em về vị trí của điểm O trong mỗi trường hợp.
Giải
a) Tan giác nhọn:
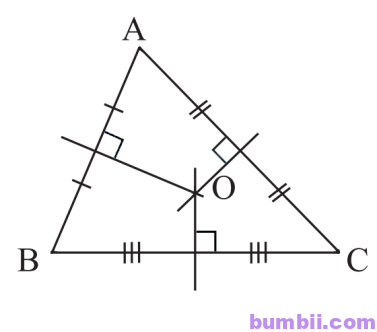
Tan giác vuông:
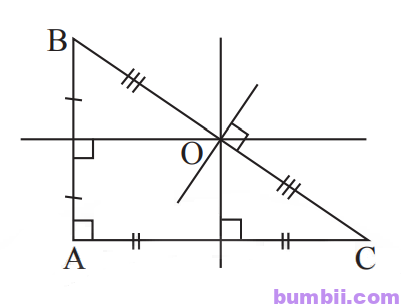
Tam giác tù:

b)

\(\)
\(2.\) Cho tam giác nhọn ABC. Gọi M, N, P lần lượt là trung điểm các cạnh AB, BC, CA và cho O là điểm cách đều ba đỉnh của tam giác ABC. Chứng minh rằng MO vuông góc với AB, NO vuông góc với BC và PO vuông góc với AC.
Giải
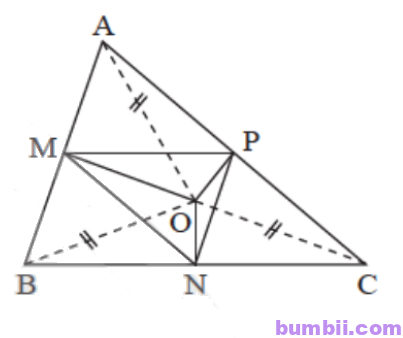
OA = OB, MA = MB suy ra MO là đường trung trực của đoạn thẳng AB, suy ra MO vuông góc với AB.
OC = OA, PC = PA suy ra PO là đường trung trực của đoạn thẳng AC, suy ra PO vuông góc với AC.
OB = OC, NB = NC suy ra NO là đường trung trực của đoạn thẳng BC, suy ra NO vuông góc với BC.
\(\)
\(3.\) Người ta muốn phục chế lại một đĩa cổ hình tròn bị vỡ chỉ còn lại một mảnh (Hình \(6\)). Làm thế nào để xác định được bán kính của đĩa cổ này.

Giải
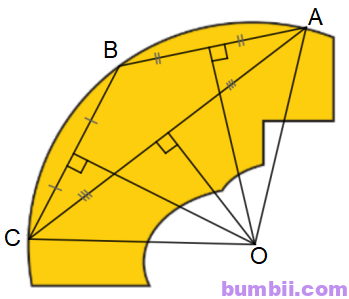
Lấy ba điểm A, B, C trên đoạn cung tròn còn lại của đĩa.
Vẽ hai đường trung trực của AB và AC.
Hai đường trung trực cắt nhau tại O, ta có bán kính R = OA = OB = OC.
\(\)
Xem bài giải trước: Bài 5: Đường trung trực của một đoạn thẳng
Xem bài giải tiếp theo: Bài 7: Tính chất ba đường trung tuyến của tam giác
Xem thêm các bài giải khác tại: Giải bài tập SGK Toán Lớp 7 – NXB Chân Trời Sáng Tạo.
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech
