Chương 2 – Bài 6: Số vô tỉ. Căn bậc hai số học trang 32 sách giáo khoa toán lớp 7 tập 1 NXB Kết nối tri thức với cuộc sống.
2.6. Cho biết \(153^2 = 23\ 409\). Hãy tính \(\sqrt{23\ 409}.\)
Giải
Ta có: \(153^2 = 23409,\ 153 > 0 \Rightarrow \sqrt{23409} = 153\)
\(\)
2.7. Từ các số là bình phương của 12 số tự nhiên đầu tiên, em hãy tìm căn bậc hai số học của các số sau:
a) 9; \(\hspace{3cm}\) b) 16;
c) 81; \(\hspace{2,8cm}\) d) 121.
Giải
a) Ta có: \(9 = 3^2,\ 3 > 0 \Rightarrow \sqrt{9} = 3\)
b) Ta có: \(16 = 4^2,\ 4 > 0 \Rightarrow \sqrt{16} = 4\)
c) Ta có: \(81 = 9^2,\ 9 > 0 \Rightarrow \sqrt{81} = 9\)
d) Ta có: \(121 = 11^2,\ 11 > 0 \Rightarrow \sqrt{121} = 11\)
\(\)
2.8. Khi tìm căn bậc hai số học của một số tự nhiên ta thường phân tích số đó ra thừa số nguyên tố. Chẳng hạn:
Vì \(324 = 2^2 . 3^4 = (2 . 3^2)^2 = 18^2\) nên \(\sqrt{324} = 18.\)
Tính căn bậc hai số học của \(129\ 600.\)
Giải
Cách 1: \(129\ 600=1\ 296\ .\ 100=2^4.3^4.10^2\) \(=4^2.9^2.10^2=(4.9.10)^2=360^2.\)
\(\Rightarrow \sqrt{129\ 600}=\sqrt{360^2}=360.\)
Cách 2: \(129600 = 2^6 . 3^4 . 5^2 = 8^2.9^2.5^2\) \(= (8.9.5)^2 = 360^2.\)
\(\Rightarrow \sqrt{129\ 600}=\sqrt{360^2}=360.\)
\(\)
2.9. Tính độ dài cạnh của hình vuông có diện tích bằng:
a) \(81\ dm^2;\)
b) \(3\ 600\ m^2;\)
c) 1 ha.
Giải
a) Độ dài các cạnh của hình vuông là: \(\sqrt{81}=9\) (dm)
b) Độ dài các cạnh của hình vuông là: \(\sqrt{3\ 600}=60\) (m).
c) Đổi \(1\ ha = 10\ 000\ m^2\)
Độ dài các cạnh của hình vuông là: \(\sqrt{10\ 000}=100\) (m).
\(\)
2.10. Sử dụng máy tính cầm tay tìm căn bậc hai số học của các số sau rồi làm tròn các kết quả với độ chính các 0,005.
a) 3; \(\hspace{2cm}\) b) 41; \(\hspace{2cm}\) c) \(2\ 021.\)
Giải
Làm tròn các kết quả với độ chính xác \(0,005\) tức là làm tròn đến hàng phần trăm.
a) \(\sqrt{3}=1,73205… \approx 1,73\)
b) \(\sqrt{41}=6,40312… \approx 6,40\)
c) \(\sqrt{2021}=44,95553… \approx 44,96\)
\(\)
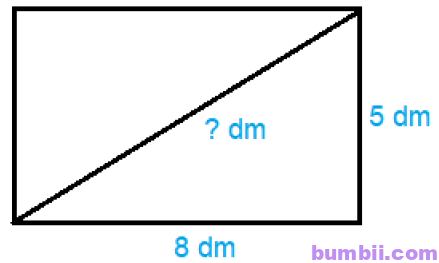
2.11. Biết rằng bình phương độ dài đường chéo của một hình chữ nhật bằng tổng các bình phương độ dài hai cạnh của nó. Một hình chữ nhật có chiều dài 8 dm và chiều rộng là 5 dm. Độ dài đường chéo của hình chữ nhật đó bằng bao nhiêu đềximét? (làm tròn kết quả đến hàng phần mười).
Giải
Bình phương độ dài đường chéo của hình chữ nhật là: \(8^2 + 5^2 = 64 + 25 = 89.\)
Độ dài đường chéo của hình chữ nhật là: \(\sqrt{89}=9,43398…\) (dm).
Làm tròn kết quả đến hàng phần mười được \(\sqrt{89} \approx 9,4.\)
Vậy đường chéo hình chữ nhật dài xấp xỉ \(9,4\) dm.
\(\)
2.12. Để lát một mảnh sân hình vuông có diện tích \(100\ m^2\), người ta cần dùng bao nhiêu viên gạch hình vuông có cạnh dài 50 cm (coi các mạch ghép là không đáng kể)?
Giải
Đổi \(50\ cm = 0,5\ m\)
Diện tích một viên gạch hình vuông là:
\(0,5^2 = 0,25\ (m^2).\)
Số viên gạch cần dùng để lát hết mảnh sân là:
\(100 : 0,25 = 400\) (viên gạch)
Vậy cần \(400\) viên gạch hình vuông cạnh \(50\) cm để lát hết mảnh sân.
\(\)
Xem bài giải trước: Bài 5: Làm quen với số thập phân vô hạn tuần hoàn
Xem bài giải tiếp theo: Bài 7: Tập hợp các số thực
Xem thêm các bài giải khác tại: Giải Bài tập SGK Toán Lớp 7 – NXB Kết Nối Tri Thức Với Cuộc Sống
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech
