Bài \(3\). Đường tròn trong mặt phẳng toạ độ trang \(59\) SGK toán lớp \(10\) tập \(2\) Nhà xuất bản Chân trời sáng tạo. Các em cùng Bumbii giải các bài tập sau.
Bài \(1\). Phương trình nào trong các phương trình sau đây là phương trình đường tròn? Tìm toạ độ tâm và bán kính của đường tròn đó.
\(a)\) \(x^2 + y^2 \ – \ 6x \ – \ 8y + 21 = 0\);
\(b)\) \(x^2 + y^2 \ – \ 2x + 4y + 2 = 0\);
\(c)\) \(x^2 + y^2 \ – \ 3x + 2y + 7 = 0\);
\(d)\) \(2x^2 + 2y^2 + x + y \ – \ 1 = 0\).
Trả lời:
\(a)\) Phương trình đã cho có dạng \(x^2 + y^2 \ – \ 2ax \ – \ 2by + c = 0\) với \(a = 3, b = 4, c = 21\)
Ta có: \(a^2 + b^2 \ – \ c = 3^2 + 4^2 \ – \ 21 = 4 > 0\).
Vậy phương trình đã cho là phương trình đường tròn có tâm \(I(3; 4)\) và bán kính \(R = \sqrt{4} = 2\).
\(b)\) Phương trình đã cho có dạng \(x^2 + y^2 \ – \ 2ax \ – \ 2by + c = 0\) với \(a = 1, b = \ – \ 2, c = 2\)
Ta có: \(a^2 + b^2 \ – \ c = 1^2 + (\ – \ 2)^2 \ – \ 2 = 3 > 0\).
Vậy phương trình đã cho là phương trình đường tròn có tâm \(I(1; \ – \ 2)\) và bán kính \(R = \sqrt{3}\)
\(c)\) Phương trình đã cho có dạng \(x^2 + y^2 \ – \ 2ax \ – \ 2by + c = 0\) với \(a = \displaystyle \frac{3}{2}, b = \ – \ 1, c = 7\)
Ta có: \(a^2 + b^2 \ – \ c = \left(\displaystyle \frac{3}{2} \right)^2 + (\ – \ 1)^2 \ – \ 7 = \ – \ \displaystyle \frac{15}{4} < 0\).
Vậy phương trình đã cho không là phương trình đường tròn.
\(d)\) \(2x^2 + 2y^2 + x + y \ – \ 1 = 0\)
\(\Leftrightarrow x^2 + y^2 + \displaystyle \frac{1}{2}x + \displaystyle \frac{1}{2}y \ – \ \displaystyle \frac{1}{2} = 0\)
Phương trình đã cho có dạng \(x^2 + y^2 \ – \ 2ax \ – \ 2by + c = 0\) với \(a = \ – \ \displaystyle \frac{1}{4}, b = \ – \ \displaystyle \frac{1}{4}, c = \ – \ \displaystyle \frac{1}{2}\)
Ta có: \(a^2 + b^2 \ – \ c = \left(\ – \ \displaystyle \frac{1}{4} \right)^2 + \left( \ – \ \displaystyle \frac{1}{4} \right)^2 + \displaystyle \frac{1}{2} = \displaystyle \frac{5}{8} > 0\)
Vậy phương trình đã cho là phương trình đường tròn có tâm \(I \left(\ – \ \displaystyle \frac{1}{4}; \ – \ \displaystyle \frac{1}{4} \right)\) và bán kính \(R = \sqrt{\displaystyle \frac{5}{8}}\)
\(\)
Bài \(2\). Lập phương trình đường tròn \((C)\) trong các trường hợp sau:
\(a)\) \((C)\) có tâm \(I(1; 5)\) và có bán kính \(r = 4\);
\(b)\) \((C)\) có đường kính \(MN\) với \(M(3; \ – \ 1)\) và \(N(9; 3)\).
\(c)\) \((C)\) có tâm \(I(2; 1)\) và tiếp xúc với đường thẳng \(5x \ – \ 12y + 11 = 0\);
\(d)\) \((C)\) có tâm \(A(1; \ – \ 2)\) và đi qua điểm \(B(4; \ – \ 5)\).
Trả lời:
\(a)\) Phương trình đường tròn \((C)\) có tâm \(I(1; 5)\) và có bán kính \(r = 4\) là:
\((x \ – \ 1)^2 + (y \ – \ 5)^2 = 4^2\)
\(\Leftrightarrow (x \ – \ 1)^2 + (y \ – \ 5)^2 = 16\)
Vậy phương trình đường tròn \((C)\) có tâm \(I(1; 5)\) và có bán kính \(r = 4\) là \((x \ – \ 1)^2 + (y \ – \ 1)^2 = 16\).
\(b)\) Ta có tâm \(I\) của đường tròn \(C\) là trung điểm của đoạn \(MN\)
Khi đó toạ độ điểm \(I\) là \(I(\displaystyle \frac{3 + 9}{2}; \displaystyle \frac{(\ – \ 1) + 3}{2}) = (6; 1)\)
Ta lại có: \(\overrightarrow{MN} = (6; 4)\)
\(\Rightarrow MN = \sqrt{6^2 + 4^2} = \sqrt{52}\)
Vì đường tròn \((C)\) có đường kính \(MN\) nên bán kính của đường tròn \((C)\) là: \(R = \displaystyle \frac{MN}{2} = \displaystyle \frac{\sqrt{52}}{2}\)
Vậy phương trình đường tròn \((C)\) có tâm \(I(6; 1)\) và có bán kính bằng \(\displaystyle \frac{\sqrt{52}}{2}\) là:
\((x \ – \ 6)^2 + (y \ – \ 1)^2 = \left(\displaystyle \frac{\sqrt{52}}{2} \right)^2\)
\(\Leftrightarrow (x \ – \ 6)^2 + (y \ – \ 1)^2 = 13\)
\(c)\) Đường tròn \((C)\) có tâm \(I(2; 1)\) và tiếp xúc với đường thẳng \(5x \ – \ 12y + 11 = 0\) nên bán kính của đường tròn bằng khoảng cách từ tâm \(I\) đến đường thẳng \(5x \ – \ 12y + 11 = 0\) và bằng:
\(\displaystyle \frac{|5. 2 \ – \ 12. 1 + 11|}{\sqrt{5^2 + (\ – \ 12)^2}} = \displaystyle \frac{9}{13}\)
Phương trình đường tròn \((C)\) có tâm \(I(2; 1)\) và bán kính \(R = \displaystyle \frac{9}{13}\) là:
\((x \ – \ 2)^2 + (y \ – \ 1)^2 = \left(\displaystyle \frac{9}{13} \right)^2\)
\(\Leftrightarrow (x \ – \ 2)^2 + (y \ – \ 1)^2 = \displaystyle \frac{81}{169}\)
Vậy phương trình đường tròn \((C)\) cần tìm là:
\((x \ – \ 2)^2 + (y \ – \ 1)^2 = \displaystyle \frac{81}{169}\)
\(d)\) Đường tròn \((C)\) có tâm \(A(1; \ – \ 2)\) và đi qua điểm \(B(4; \ – \ 5)\) nên bán kính đường tròn chính là đoạn thẳng \(AB\)
Ta có: \(\overrightarrow{AB} = (3; \ – \ 3)\)
\(\Rightarrow AB = \sqrt{3^2 + (\ – \ 3)^2} = 3\sqrt{2}\)
Khi đó bán kính \(R = AB = 3\sqrt{2}\)
Phương trình đường tròn tâm \(A(1; \ – \ 2)\), bán kính \(R = 3\sqrt{2}\) là:
\((x \ – \ 1)^2 + (y + 2)^2 = (3\sqrt{2})^2\)
\(\Leftrightarrow (x \ – \ 1)^2 + (y + 3)^2 = 18\)
Vậy phương trình đường tròn \((C)\) cần tìm là: \((x \ – \ 1)^2 + (y + 3)^2 = 18\)
\(\)
Bài \(3\). Lập phương trình đường tròn ngoại tiếp tam giác có toạ độ các đỉnh là:
\(a)\) \(M(2; 5), N(1; 2); P(5; 4)\);
\(b)\) \(A(0; 6), B(7; 7), C(8; 0)\).
Trả lời:
\(a)\) Gọi \((C)\) là đường tròn ngoại tiếp tam giác \(MNP\) có tâm \(I(a; b)\) và bán kính \(R\)
Khi đó: \(MI = NI = PI\)
Lại có: \(MI = \sqrt{(a \ – \ 2)^2 + (b \ – \ 5)^2}\)
\(NI = \sqrt{(a \ – \ 1)^2 + (b \ – \ 2)^2}\)
\(PI = \sqrt{(a \ – \ 5)^2 + (b \ – \ 4)^2}\)
Ta có hệ phương trình sau:
\(\left \{\begin{matrix} MI = NI\\MI = PI \end{matrix} \right.\)
\(\Leftrightarrow \left \{\begin{matrix} \sqrt{(a \ – \ 2)^2 + (b \ – \ 5)^2} = \sqrt{(a \ – \ 1)^2 + (b \ – \ 2)^2}\\\sqrt{(a \ – \ 2)^2 + (b \ – \ 5)^2} = \sqrt{(a \ – \ 5)^2 + (b \ – \ 4)^2} \end{matrix} \right.\)
\(\Leftrightarrow \left \{\begin{matrix} (a \ – \ 2)^2 + (b \ – \ 5)^2 = (a \ – \ 1)^2 + (b \ – \ 2)^2\\ (a \ – \ 2)^2 + (b \ – \ 5)^2= (a \ – \ 5)^2 + (b \ – \ 4)^2 \end{matrix} \right.\)
\(\Leftrightarrow \left \{\begin{matrix} a^2 + b^2 \ – \ 4a \ – \ 10b + 29 = a^2 + b^2 \ – \ 2a \ – \ 4b + 5\\a^2 + b^2 \ – \ 4a \ – \ 10b + 29 = a^2 + b^2 \ – \ 10a \ – \ 8b + 41 \end{matrix} \right.\)
\(\Leftrightarrow \left \{\begin{matrix}a + 3b = 12\\3a \ – \ b = 6 \end{matrix} \right.\)
\(\Leftrightarrow \left \{\begin{matrix}a = 3\\b = 3 \end{matrix} \right.\)
Suy ra tâm \(I(3; 3)\) và bán kính \(R = MI = \sqrt{(3 \ – \ 2)^2 + (3 \ – \ 5)^2} = \sqrt{5}\)
Phương trình đường tròn ngoại tiếp tam giác \(MNP\) có tâm \(I(3; 3)\) và có bán kính \(R = \sqrt{5}\) là:
\((x \ – \ 3)^2 + (y \ – \ 3)^2 = 5\)
\(b)\) Gọi \((C)\) là đường tròn ngoại tiếp tam giác \(ABC\) có tâm \(I(a; b)\) và bán kính \(R\)
Khi đó: \(AI = BI = CI\)
Lại có: \(AI = \sqrt{a^2 + (b \ – \ 6)^2}\)
\(BI = \sqrt{(a \ – \ 7)^2 + (b \ – \ 7)^2}\)
\(CI = \sqrt{(a \ – \ 8)^2 + b^2}\)
Ta có hệ phương trình sau:
\(\left \{\begin{matrix} AI = BI\\AI = CI \end{matrix} \right.\)
\(\Leftrightarrow \left \{\begin{matrix} \sqrt{a^2 + (b \ – \ 6)^2} = \sqrt{(a \ – \ 7)^2 + (b \ – \ 7)^2}\\\sqrt{a^2 + (b \ – \ 6)^2} = \sqrt{(a \ – \ 8)^2 + b^2} \end{matrix} \right.\)
\(\Leftrightarrow \left \{\begin{matrix} a^2 + (b \ – \ 6)^2 =(a \ – \ 7)^2 + (b \ – \ 7)^2\\ a^2 + (b \ – \ 6)^2 = (a \ – \ 8)^2 + b^2 \end{matrix} \right.\)
\(\Leftrightarrow \left \{\begin{matrix} a^2 + b^2 \ – \ 12b + 36 = a^2 + b^2 \ – \ 14a \ – \ 14b + 98\\a^2 + b^2 \ – \ 12b + 36 = a^2 + b^2 \ – \ 16a + 64 \end{matrix} \right.\)
\(\Leftrightarrow \left \{\begin{matrix}14a + 2b = 62\\16a \ – \ 12b = 28 \end{matrix} \right.\)
\(\Leftrightarrow \left \{\begin{matrix}a = 4\\b = 3 \end{matrix} \right.\)
Suy ra tâm \(I(4; 3)\) và bán kính \(R = AI = \sqrt{4^2 + (3 \ – \ 6)^2} = \sqrt{25} = 5\)
Phương trình đường tròn ngoại tiếp tam giác \(ABC\) có tâm \(I(4; 3)\) và có bán kính \(R = 5\) là:
\((x \ – \ 4)^2 + (y \ – \ 3)^2 = 25\).
\(\)
Bài \(4\). Lập phương trình đường tròn tiếp xúc với hai trục toạ độ \(Ox, Oy\) và đi qua điểm \(A(4; 2)\).
Trả lời:
Gọi \(I(a; b)\) là tâm đường tròn cần tìm
Ta có: \(d(I, Ox) = b; d(I, Oy) = a\)
Lại có bán kính đường tròn \(R = IA = \sqrt{(4 \ – \ a)^2 + (2 \ – \ b)^2}\)
Đường tròn tiếp xúc với hai trục toạ độ \(Ox, Oy\) nên khoảng cách từ tâm \(I\) đến hai trục chính là bán kính của đường tròn \((a = b = R)\).
Suy ra ta có hệ phương trình:
\(\left \{\begin{matrix}b = \sqrt{(4 \ – \ a)^2 + (2 \ – \ b)^2}\\a = \sqrt{(4 \ – \ a)^2 + (2 \ – \ b)^2} \end{matrix} \right.\)
Thay \(a = b\) vào phương trình \(\sqrt{(4 \ – \ a)^2 + (2 \ – \ b)^2}\) ta được:
\(a = \sqrt{(4 \ – \ a)^2 + (2 \ – \ a)^2}\)
\(\Rightarrow a^2 = (4 \ – \ a)^2 + (2 \ – \ a)^2\)
\(\Rightarrow a^2 \ – \ 12a + 20 = 0\)
\(\Rightarrow \left[ \begin{matrix}a = 2\\a = 10 \end{matrix} \right.\)
Thay các nghiệm vừa tìm được vào phương trình \(a = \sqrt{(4 \ – \ a)^2 + (2 \ – \ a)^2}\) ta thấy đều thoả mãn.
Với \(a = b = 2\) ta được phương trình đường tròn \((C)\) là:
\((x \ – \ 2)^2 + (y \ – \ 2)^2 = 4\)
Với \(a = b = 10\) ta được phương trình đường tròn \((C)\) là:
\((x \ – \ 10)^2 + (y \ – \ 10)^2 = 100\).
\(\)
Bài \(5\). Cho đường tròn \((C)\) có phương trình: \(x^2 + y^2 \ – \ 2x \ – \ 4y \ – \ 20 = 0\).
\(a)\) Chứng tỏ rằng điểm \(M(4; 6)\) thuộc đường tròn \((C)\).
\(b)\) Viết phương trình tiếp tuyến của \((C)\) tại điểm \(M(4; 6)\).
\(c)\) Viết phương trình tiếp tuyến của \((C)\) song song với đường thẳng \(4x + 3y + 2022 = 0\).
Trả lời:
\(a)\) Thay toạ độ điểm \(M(4; 6)\) vào phương trình đường tròn \((C)\) ta có:
\(4^2 + 6^2 \ – \ 2. 4 \ – \ 4. 6 \ – \ 20 = 16 + 36 \ – \ 8 \ – \ 24 \ – \ 20 = 0\)
Suy ra điểm \(M\) thuộc đường tròn \((C)\) (đpcm)
\(b)\) Đường tròn \((C)\) có tâm \(I(1; 2)\)
Phương trình tiếp tuyến của \((C)\) tại \(M(4; 6)\) là:
\((1 \ – \ 4)(x \ – \ 4) + (2 \ – \ 6)(y \ – \ 6) = 0\)
\(\Leftrightarrow \ – \ 3x + 12 \ – \ 4y + 24 = 0\)
\(\Leftrightarrow 3x + 4y \ – \ 36 = 0\)
\(c)\) Tiếp tuyến của đường tròn song song với đường thẳng \(4x + 3y + 2022 = 0\) nên phương trình có dạng \(\Delta\): \(4x + 3y + c = 0\)
Đường tròn \((C)\) có tâm \(I(1; 2)\) và bán kính \(R = \sqrt{1^2 + 2^2 \ – \ (\ – \ 20)} = 5\)
Khoảng cách từ tâm \(I\) đến tiếp tuyến chính là bán kính đường tròn nên ta có:
\(d(I; \Delta) = \displaystyle \frac{|4. 1 + 3. 2 + c|}{\sqrt{4^2 + 3^2}} = 5\)
\(\Rightarrow \left[ \begin{matrix}c = 15\\c = \ – \ 35 \end{matrix} \right.\)
Vậy có hai tiếp tuyến cần tìm là:
\(\Delta_1 = 4x + 3y + 15 = 0, \Delta_2 = 4x + 3y \ – \ 35 = 0\).
\(\)
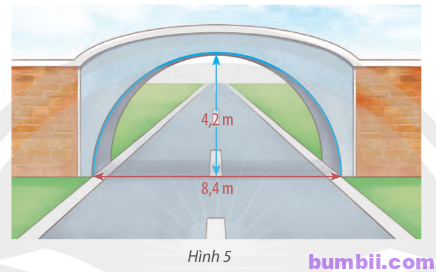
Bài \(6\). Một cái cổng hình bán nguyệt rộng \(8,4 m\), cao \(4,2 m\) như Hình \(5\). Mặt đường dưới cổng được chia thành hai làn cho xe ra vào.
\(a)\) Viết phương trình mô phỏng cái cổng.
\(b)\) Một chiếc xe tải rộng \(2,2 m\) và cao \(2,6 m\) đi đúng làn đường quy định có thể đi qua cổng mà không làm hư hỏng cổng hay không?
Trả lời:
\(a)\) Ta thấy cổng hình bán nguyệt có chiều cao bằng nửa chiều rộng của đường nên cổng có dạng nửa đường tròn.
Gắn trục toạ độ ở tim đường, ta có phương trình mô phỏng cái cổng là:
\(x^2 + y^2 = 4,2^2\) (\(y > 0\) vì cổng luôn nằm phía trên mặt đường)
\(b)\) Điểm cao nhất của chiếc xe có toạ độ \((2,2; 2,6)\)
Để biết xe tải đi đúng làn đường quy định có thể đi qua cổng mà không làm hư hỏng cổng hay không ta đi xét điểm cao nhất của chiếc xe có nằm trong đường tròn mô phỏng cổng hay không hay cách khác là khoảng cách từ tâm đường tròn đến điểm cao nhất của chiếc xe có nhỏ hơn bán kính đường tròn.
Ta có khoảng cách từ tâm đường tròn đến điểm cao nhất của xe là:
\(\sqrt{2,2^2 + 2,6^2} \approx 3,41\)
Ta thấy \(3,41 < R = 4,2\) nên điểm cao nhất của chiếc xe nằm bên trong đường tròn.
Vậy chiếc xe tải rộng \(2,2 m\) và cao \(2,6 m\) đi đúng làn đường quy định có thể đi qua cổng mà không làm hư hỏng cổng.
Bài 3. Đường tròn trong mặt Bài 3. Đường tròn trong mặt Bài 3. Đường tròn trong mặt
Xem bài giải trước: https://bumbii.com/bai-2-duong-thang-trong-mat-phang-toa-do/
Xem bài giải tiếp theo: https://bumbii.com/bai-4-ba-duong-conic-trong-mat-phang-toa-do/
Xem các bài giải khác: https://bumbii.com/giai-toan-lop-10-nxb-chan-troi-sang-tao
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech

Hạnh phúc đạt được khi bạn ngừng chờ đợi điều đó xảy ra và thực hiện các bước để biến nó thành hiện thực.