Bài \(1\). Điểm, đường thẳng và mặt phẳng trang \(88\) Sách giáo khoa Toán lớp \(11\) tập \(1\) Chân trời sáng tạo. Các em cùng Bumbii giải các bài tập sau:
Bài \(1\). Cho hình chóp \(S.ABCD\), gọi \(O\) là giao điểm của \(AC\) và \(BD\). Lấy \(M, N\) lần lượt thuộc các cạnh \(SA, SC\).
\(a)\) Chứng minh đường thẳng \(MN\) nằm trong mặt phẳng \((SAC)\).
\(b)\) Chứng minh \(O\) là điểm chung của hai mặt phẳng \((SAC) \text{ và } (SBD)\).
Trả lời:
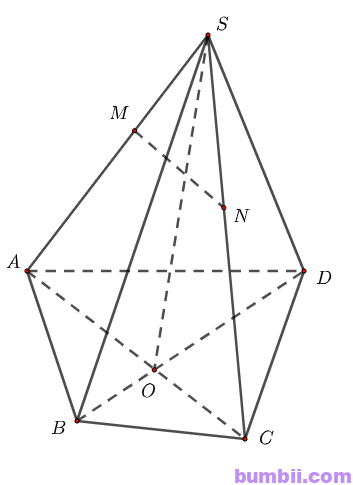
\(a)\) Ta có:
\(\left. \begin{matrix}M \in SA\\SA \subset (SAC) \end{matrix} \right\}\) \(\Rightarrow M \in (SAC)\)
\(\left. \begin{matrix}N \in SC\\SC \subset (SAC) \end{matrix} \right\} \Rightarrow N \in (SAC)\)
Vậy \(MN \in (SAC)\)
\(b)\) Ta cũng có:
\(\left. \begin{matrix} O \in AC\\AC \subset (SAC) \end{matrix} \right\} \Rightarrow O \in (SAC)\)
\(\left. \begin{matrix}O \in BD\\BD \subset (SBD) \end{matrix} \right\} \Rightarrow O \in (SBD)\)
Vậy \(O\) là điểm chung của hai mặt phẳng \((SAC) \text{ và } (SBD)\).
\(\)
Bài \(2\). Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(M\) là trung điểm của \(SC\).
\(a)\) Tìm giao điểm \(I\) của đường thẳng \(AM\) và mặt phẳng \((SBD)\). Chứng minh \(IA = 2 IM\).
\(b)\) Tìm giao điểm \(E\) của đường thẳng \(SD\) và mặt phẳng \((ABM)\).
\(b)\) Gọi \(N\) là một điểm tuỳ ý trên cạnh \(AB\). Tìm giao điểm của đường thẳng \(MN\) và mặt phẳng \((SBD)\).
Trả lời:
Gọi \(O\) là giao điểm của \(AC\) và \(BD\)
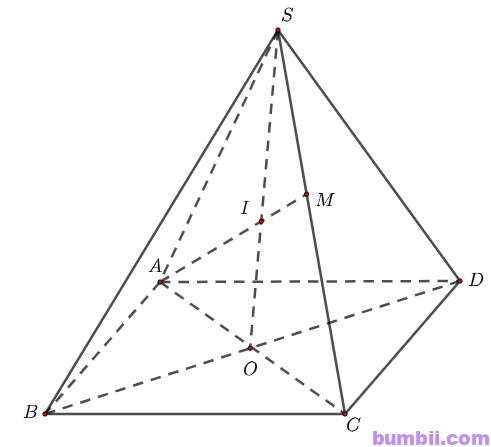
\(a)\) Gọi \(I\) là giao điểm của \(SO\) và \(AM\).
Khi đó \(I \in AM\)
Lại có: \(\left. \begin{matrix}I \in SO\\SO \subset (SBD) \end{matrix} \right\} \Rightarrow I \in (SBD)\)
Vậy \(I\) là giao điểm của \(AM\) với \((SBD)\)
Xét tam giác \(SAC\) ta có:
\(\left. \begin{matrix}\text{ O là trung điểm của AC }\\ \text{ M là trung điểm của SC }\\ \text{ SO cắt AM tại I } \end{matrix} \right\} \Rightarrow I\) là trọng tâm tam giác \(SAC\).
Suy ra \(AI = \displaystyle \frac{2}{3}AM\)
Hay \(AI = 2 IM\)
\(b)\) Trên mặt phẳng \((SCD)\), qua \(M\) dựng đường thẳng song song với \(AB\), cắt \(SD\) tại \(E\)
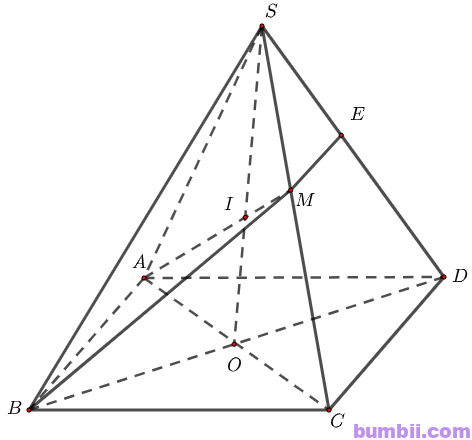
Vì \(ME // AB\) nên bốn điểm \(A, B, M, E\) thuộc cùng một mặt phẳng hay \(E \in (ABM)\)
Mặt khác \(E \in SD\)
Vậy \(E\) là giao điểm của \(SD\) và \((ABM)\).
\(c)\) Xét mặt phẳng \(ABCD\), gọi \(P\) là giao điểm của \(BD\) và \(NC\)
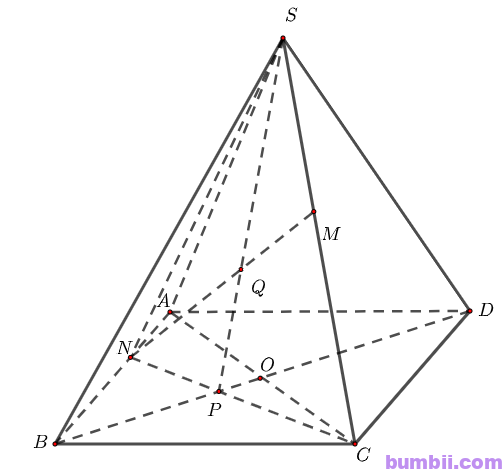
Khi đó ta có \(SP\) là giao tuyến của hai mặt phẳng \((SNC) \text{ và } (SBD)\)
Xét mặt phẳng \((SNC)\). Gọi \(Q\) là giao điểm của \(MN\) và \(SP\).
Suy ra \(Q \in SP\). Mà \(SP \subset (SBD)\) nên \(Q \in (SBD)\)
Vậy \(Q\) là giao điểm của \(MN\) và \((SBD)\)
\(\)
Bài \(3\). Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(O\) là giao điểm của \(AC\) và \(BD\); \(M, N\) lần lượt là trung điểm của \(SB, SD; P\) thuộc đoạn \(SC\) và không là trung điểm của \(SC\).
\(a)\) Tìm giao điểm \(E\) của đường thẳng \(SO\) và mặt phẳng \((MNP)\).
\(b)\) Tìm giao điểm \(Q\) của đường thẳng \(SA\) và mặt phẳng \((MNP)\).
\(c)\) Gọi \(I, J, K\) lần lượt là giao điểm của \(QM\) và \(AB\), \(QP\) và \(AC\), \(QN\) và \(AD\). Chứng minh \(I, J, K\) thẳng hàng.
Trả lời:
\(a)\) Xét trong mặt phẳng \((SBD)\). Gọi \(E\) là giao điểm của \(SO\) và \(MN\)
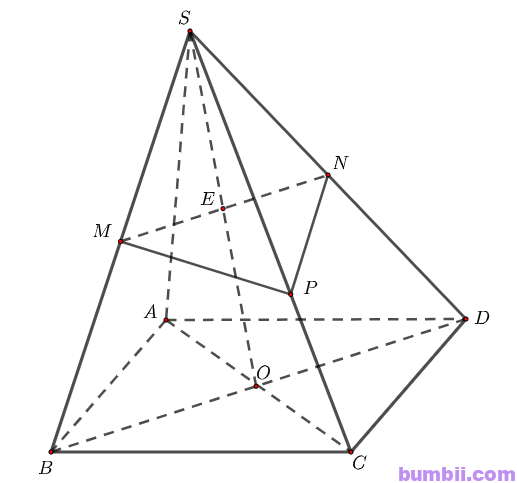
Khi đó ta có \(E \in MN\) nên \(E \in (MNP)\)
Vậy \(E\) là giao điểm của \(SO\) và \((MNP)\).
\(b)\) Xét mặt phẳng \((SAC)\). Gọi \(Q\) là giao điểm của \(PE\) và \(SA\).

Vì \(PE \in (MNP)\) nên \(Q \in (MNP)\)
Vậy \(Q\) là giao điểm của \(SA\) và \((MNP)\).
\(c)\)
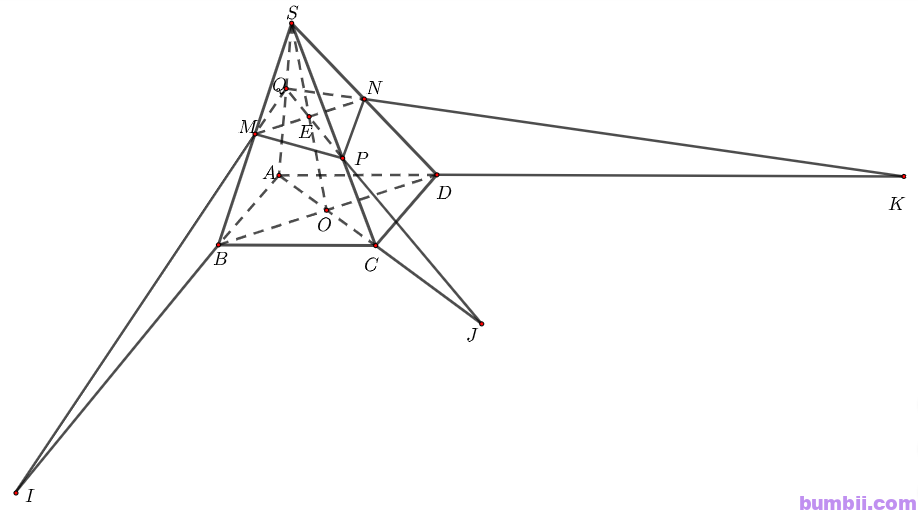
Ta có: \(I, K\) là hai điểm chung của hai mặt phẳng \((MNQ) \text{ và } (ABCD)\)
Suy ra \(IK\) là giao tuyến của hai mặt phẳng \((MNPQ) \text { và } (ABCD)\)
Lại có: \(J \in QP\) mà \(QP \subset (MNPQ)\) nên \(J \in (MNPQ)\)
\(J \in AC\) mà \(AC \subset (MNPQ)\) nên \(J \in (ABCD)\)
\(\Rightarrow J\) là giao điểm của hai mặt phẳng \((MNPQ)\) và \((ABCD)\)
\(\Rightarrow J \in\) giao tuyến \(IK\) của hai mặt phẳng \((MNPQ)\) và \((ABCD)\)
Vậy \(I, J, K\) thẳng hàng.
\(\)
Bài \(4\). Cho tứ diện \(A, B, C, D\). Gọi \(E, F, G\) lần lượt là ba điểm trên ba cạnh \(AB, AC, BD\) sao cho \(EF\) cắt \(BC\) tại \(I (I \neq C)\), \(EG\) cắt \(AD\) tại \(H (H \neq D)\).
\(a)\) Tìm giao tuyến của các mặt phẳng \((EFG) \text{ và } (BCD); (EFG) \text{ và } (ACD)\).
\(b)\) Chứng minh ba đường thẳng \(CD, IG, HF\) cùng đi qua một điểm.
Trả lời:
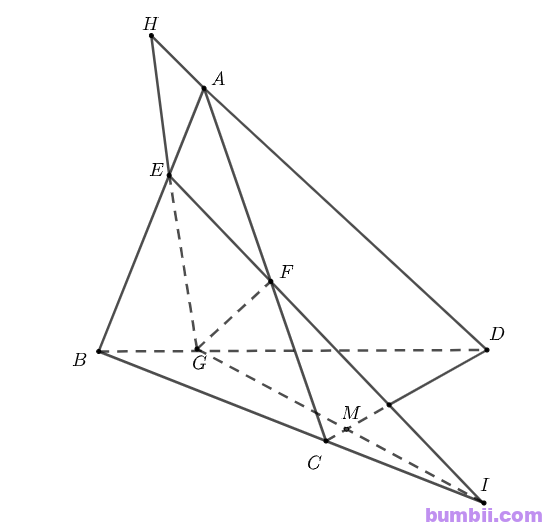
\(a)\) Ta có: \(\left. \begin{matrix}I \in BC, I \in EF\\G \in EG, G \in BD \end{matrix} \right\}\Rightarrow I, G\) là hai giao điểm của hai mặt phẳng \((EFG)\) và \((BCD)\)
Vậy \(IG\) là giao tuyến của hai mặt phẳng \((EFG)\) và \((BCD)\)
Xét mặt phẳng \((BCD)\). Gọi \(M\) là giao điểm của \(GI\) và \(CD\). Khi đó \(M \in (ACD)\)
\(\Rightarrow M, F\) là hai điểm chung của hai mặt phẳng \((EFG)\) và \((ACD)\)
Vậy \(MF\) là giao tuyến của hai mặt phẳng \((EFG)\) và \((ACD)\)
\(b)\) Ta có: \(H \in AD, AD \subset (ACD)\) nên \(H \in (ACD)\)
Lại có: \(H \in EG, EG \subset (EFG)\) nên \(H \in (EFG)\)
Suy ra \(H\) là giao điểm của hai mặt phẳng \((EFG)\) và \((ACD)\) hay \(H\) nằm trên giao tuyến \(MF\) của hai mặt phẳng \((EFG)\) và \((ACD)\)
\(\Rightarrow HF\) đi qua \(M\)
Vậy \(CD, IG, HF\) cùng đi qua điểm \(M\).
\(\)
Bài \(5\). Thước laser phát ra tia laser, khi tia này quay sẽ tạo ra mặt phẳng ánh sáng (Hình \(41\)). Giải thích tại sao các thước kẻ laser lại giúp cho người thợ xây kẻ được đường thẳng trên tường hoặc sàn nhà.

Trả lời:
Khi tia laser quay sẽ tạo ra mặt phẳng ánh sáng và mặt phẳng này sẽ giao với mặt phẳng tường hoặc sàn nhà tại một đường thẳng.
Do đó, người thợ xây khi sử dụng thước laser sẽ kẻ được đường thẳng trên tường hoặc sàn nhà (Giao tuyến của hai mặt phẳng).
Bài 1. Điểm đường thẳng và Bài 1. Điểm đường thẳng và Bài 1. Điểm đường thẳng và Bài 1. Điểm đường thẳng và
Xem bài giải trước: Bài tập cuối chương III
Xem bài giải tiếp theo: Bài 2 – Hai đường thẳng song song
Xem các bài giải khác: Giải bài tập SGK Toán Lớp 11 Chân trời sáng tạo
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech

Hạnh phúc đạt được khi bạn ngừng chờ đợi điều đó xảy ra và thực hiện các bước để biến nó thành hiện thực.