Chương 7 – Bài 10: Tính chất ba đường trung tuyến của tam giác trang 107 sách giáo khoa toán lớp 7 tập 2 NXB Cánh Diều. Các em cùng Bumbii giải các bài tập sau.
1. Cho tam giác ABC. Ba đường trung tuyến AM, BN, CP đồng quy tại G. Chứng minh:
GA + GB + GC = \(\displaystyle\frac{2}{3}\)(AM + BN + CP)
Giải

Ba đường trung tuyến AM, BN, CP cắt nhau tại G nên G là trọng tâm của tam giác ABC.
Suy ra \(GA = \displaystyle\frac{2}{3} AM;\) \(GB = \displaystyle\frac{2}{3} BN;\) \(GC = \displaystyle\frac{2}{3} CP.\)
Do đó GA + GB + GC = \(\displaystyle\frac{2}{3}\)(AM + BN + CP)
\(\)
2. Cho tam giác ABC cân tại A, hai đường trung tuyến BM và CN cắt nhau tại G. Chứng minh:
a) BM = CN;
b) ∆GBC cân tại G.
Giải
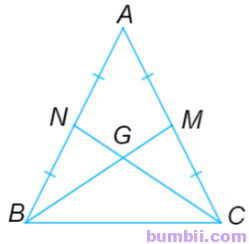
a) Tam giác ABC cân tại A nên AB = AC và \(\widehat{ABC} = \widehat{ACB}.\)
Do BM và CN là hai đường trung tuyến của ∆ABC nên M là trung điểm của AC và N là trung điểm của AB.
Do đó BN = MC.
Xét hai tam giác NBC và MCB có:
BN = MC (chứng minh trên);
\(\widehat{NBC} = \widehat{MCB}\) (chứng minh trên);
BC là cạnh chung.
Do đó ∆NBC = ∆MCB (c.g.c).
Suy ra BM = CN (hai cạnh tương ứng).
b) Tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại G nên G là trọng tâm của ∆ABC.
Suy ra \(GB = \displaystyle\frac{2}{3} BM;\) \(GC = \displaystyle\frac{2}{3} CN.\)
Mà BM = CN nên GB = GC.
Do GB = GC nên ∆GBC cân tại G.
\(\)
3. Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Trên tia đối của tia MA lấy điểm D sao cho MD = MG. Chứng minh:
a) GA = GD;
b) ∆MBG = ∆MCD;
c) CD = 2GN.
Giải

a) Tam giác ABC có hai đường trung tuyến AM, BN cắt nhau tại G nên G là trọng tâm của tam giác ABC.
Suy ra \(GM = \displaystyle\frac{1}{2} GA.\)
Trên tia đối của tia MA lấy điểm D sao cho MD = MG nên M là trung điểm của GD.
Suy ra \(GM = \displaystyle\frac{1}{2} GD.\)
Vậy GA = GD.
b) Do M là trung điểm của GD nên MG = MD.
Xét hai tam giác MBG và MCD có:
MB = MC (giả thiết).
\(\widehat{GMB} = \widehat{DMC}\) (hai góc đối đỉnh).
MG = MD (chứng minh trên).
Do đó ∆MBG = ∆MCD (c.g.c).
c) Do ∆MBG = ∆MCD (c.g.c) nên CD = BG (hai cạnh tương ứng).
Do G là trọng tâm của tam giác ABC nên BG = 2GN.
Mà CD = BG nên CD = 2GN.
\(\)
4. Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Gọi H là hình chiếu của A lên đường thẳng BC. Giả sử H là trung điểm của đoạn thẳng BM. Chứng minh:
a) ∆AHB = ∆AHM;
b) \(AG = \displaystyle\frac{2}{3} AB.\)
Giải
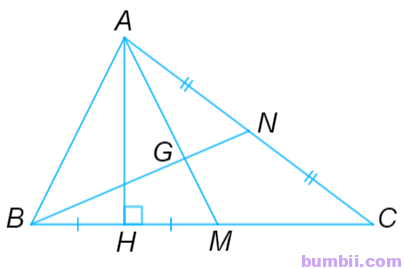
a) Do H là hình chiếu của A trên BC nên AH ⊥ BC.
Xét hai tam giác vuông AHB và AHM có:
AH là cạnh chung.
HB = HM (giả thiết).
Do đó ∆AHB = ∆AHM (hai cạnh góc vuông).
b) Do ∆AHB = ∆AHM nên AB = AM (hai cạnh tương ứng).
Hai đường trung tuyến AM, BN cắt nhau tại G nên G là trọng tâm của ∆ABC.
Suy ra AG = \(\displaystyle\frac{2}{3}\)AM mà AB = AM
Vậy AG = \(\displaystyle\frac{2}{3}\)AM.
\(\)
5. Hình 107 là mặt cắt đứng của một ngôi nhà có mái dốc. Mỗi tầng cao 3,3 m. Mặt cắt mái nhà có dạng tam giác ABC cân tại A với đường trung tuyến AH dài 1,2 m. Tại vị trí O là trọng tâm tam giác ABC, người ta làm tâm cho một cửa sổ có dạng hình tròn.

a) AH có vuông góc với BC không? Vì sao?
b) Vị trí O ở độ cao bao nhiêu mét so với mặt đất?
Giải
a) ∆ABC cân tại A nên AB = AC và \(\widehat{ABH} = \widehat{ACH}\)
AH là đường trung tuyến của \(∆ABC\) nên H là trung điểm của BC.
Do đó BH = CH.
Xét hai tam giác ABH và ACH có:
AB = AC (chứng minh trên);
\(\widehat{ABH} = \widehat{ACH}\) (chứng minh trên);
BH = CH (chứng minh trên).
Do đó ∆ABH = ∆ACH (c.g.c).
Suy ra \(\widehat{AHB} = \widehat{AHC}\) (hai góc tương ứng).
Mà \(\widehat{AHB} + \widehat{AHC} = 180^o\) \(\Rightarrow \widehat{AHB} = \widehat{AHC} = 90^o\) hay AH ⊥ BC.
b) Do O là trọng tâm của ∆ABC nên \(OH = \displaystyle\frac{1}{3}AH = \displaystyle\frac{1}{3} . 1,2 = 0,4\ m.\)
Do mỗi tầng cao \(3,3\ m\) nên vị trí O ở độ cao \(0,4 + 3,3 . 3 = 10,3\ m\) so với mặt đất.
\(\)
Xem bài giải trước: Bài 9: Đường trung trực của một đoạn thẳng
Xem bài giải tiếp theo: Bài 11: Tính chất ba đường phân giác của tam giác
Xem thêm các bài giải khác tại: Giải bài tập SGK Toán Lớp 7 Cánh Diều
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech
