Bài 2. Các phép toán với đa thức nhiều biến

Chương 1 – Bài 2. Các phép toán với đa thức nhiều biến trang 17 SGK toán lớp 8 tập 1 NXB Chân Trời Sáng Tạo. Các em hãy cùng Bumbii giải các bài tập sau.

1. Tính:

a) \(x+2y+(x-y);\)

b) \(2x-y-(3x-5y);\)

c) \(3x^2-4y^2+6xy+7+(-x^2+y^2-8xy\) \(+9x+1);\)

d) \(4x^2y-2xy^2+8-(3x^2y+9xy^2-12xy+6).\)

Giải

a) \(x+2y+(x-y)\)

\(=x+2y+x-y\)

\(=(x+x)+(2y-y)\)

\(=2x+y.\)

b) \(2x-y-(3x-5y)\)

\(=2x-y-3x+5y\)

\(=(2x-3x)+(5y-y)\)

\(=-x+4y\)

c) \(3x^2-4y^2+6xy+7+(-x^2+y^2\) \(-8xy+9x+1)\)

\(=3x^2-4y^2+6xy+7-x^2+y^2-8xy\) \(+9x+1\)

\(=(3x^2-x^2)-(4y^2-y^2)+(6xy-8xy)\) \(+9x+(7+1)\)

\(=2x^2-3y^2-2xy+9x+8.\)

d) \(4x^2y-2xy^2+8-(3x^2y+9xy^2-12xy+6)\)

\(=4x^2y-2xy^2+8-3x^2y-9xy^2+12xy-6\)

\(=(4x^2y-3x^2y)-(2xy^2+9xy^2)+12xy\) \(+(8-6)\)

\(=x^2y-11xy^2+12xy+2.\)

\(\)

2. Tìm độ dài cạnh còn thiếu của tam giác ở Hình 7, biết rằng tam giác có chu vi bằng \(7x+5y.\)

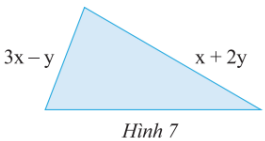
Giải

Độ dài cạnh còn thiếu của tam giác là:

\(7x+5y-(3x-y+x+2y)\)

\(=7x+5y-3x+y-x-2y\)

\(=(7x-3x-x)+(5y+y-2y)\)

\(=3x+4y.\)

\(\)

3. Thực hiện phép nhân.

a) \(3x(2xy-5x^2y);\)

b) \(2x^2y(xy-4xy^2+7y);\)

c) \(\left(-\displaystyle\frac{2}{3}xy^2+6yz^2\right).\left(-\displaystyle\frac{1}{2}xy\right).\)

Giải

a) \(3x(2xy-5x^2y)\)

\(=3x\ .\ 2xy-3x\ .\ 5x^2y\)

\(=(3.2).(x.x).y-(3.5).(x.x^2).y\)

\(=6x^2y-15x^3y.\)

b) \(2x^2y(xy-4xy^2+7y)\)

\(=2x^2y\ .\ xy-2x^2y\ .\ 4xy^2+2x^2y\ .\ 7y\)

\(=2.(x^2.x).(y.y)-(2.4)(x^2.x).(y.y^2)\) \(+ (2.7).x^2.(y.y)\)

\(=2x^3y^2-8x^3y^3+14x^2y^2.\)

c) \(\left(-\displaystyle\frac{2}{3}xy^2+6yz^2\right).\left(-\displaystyle\frac{1}{2}xy\right)\)

\(=-\displaystyle\frac{2}{3}xy^2.\left(-\displaystyle\frac{1}{2}xy\right)+6yz^2.\left(-\displaystyle\frac{1}{2}xy\right)\)

\(=\left[-\displaystyle\frac{2}{3}.\left(-\displaystyle\frac{1}{2}\right)\right].(x.x).(y^2.y)\) \(+\left[6.\left(-\displaystyle\frac{1}{2}\right)\right].x.(y.y).z^2\)

\(=\displaystyle\frac{1}{3}x^2y^3-3xy^2z^2.\)

\(\)

4. Thực hiện phép nhân.

a) \((x-y)(x-5y);\)

b) \((2x+y)(4x^2-2xy+y^2).\)

Giải

a) \((x-y)(x-5y)\)

\(=x.(x-5y)-y.(x-5y)\)

\(=x^2-5xy-xy+5y^2\)

\(=x^2-6xy+5y^2.\)

b) \((2x+y)(4x^2-2xy+y^2)\)

\(=2x.(4x^2-2xy+y^2)+y.(4x^2-2xy+y^2)\)

\(=8x^3-4x^2y+2xy^2+4x^2y-2xy^2+y^3\)

\(=8x^3-4x^2y+4x^2y+2xy^2-2xy^2+y^3\)

\(=8x^3+y^3.\)

\(\)

5. Thực hiện phép chia.

a) \(20x^3y^5:(5x^2y^2);\)

b) \(18x^3y^5:[3(-x)^3y^2].\)

Giải

a) \(20x^3y^5:(5x^2y^2)\)

\(=(20:5).(x^3:x^2).(y^5:y^2)\)

\(=4xy^3.\)

b) \(18x^3y^5:[3(-x)^3y^2]\)

\(=[18:(-3)].(x^3:x).(y^5:y^2)\)

\(=-6y^3.\)

\(\)

6. Thực hiện phép chia.

a) \((4x^3y^2-8x^2y+10xy):(2xy);\)

b) \((7x^4y^2-2x^2y^2-5x^3y^4):(3x^2y).\)

Giải

a) \((4x^3y^2-8x^2y+10xy):(2xy)\)

\(=(4x^3y^2:2xy)+(-8x^2y:2xy)\) \(+(10xy:2xy)\)

\(=(4:2).(x^3:x).(y^2:y)\) \(+(-8:2).(x^2:x).(y:y)\) \(+(10:5).(x:x).(y:y)\)

\(=2x^2y-4x+5.\)

b) \((7x^4y^2-2x^2y^2-5x^3y^4):(3x^2y)\)

\(=(7x^4y^2:3x^2y)+(-2x^2y^2:3x^2y)\) \(+(-5x^3y^4:3x^2y)\)

\(=(7:3).(x^4:x^2).(y^2:y)\) \(+(-2:3).(x^2:x^2).(y^2:y)\) \(+(-5:3).(x^3:x^2).(y^4:y)\)

\(=\displaystyle\frac{7}{3}x^2y-\displaystyle\frac{2}{3}y-\displaystyle\frac{5}{3}xy^3.\)

\(\)

7. Tính giá trị của biểu thức.

a) \(3x^2y-(3xy-6x^2y)+(5xy-9x^2y)\) tại \(x=\displaystyle\frac{2}{3},\ y=-\displaystyle\frac{3}{4};\)

b) \(x(x-2y)-y(y^2-2x)\) tại \(x = 5,\ y = 3.\)

Giải

a) \(3x^2y-(3xy-6x^2y)+(5xy-9x^2y)\)

\(=3x^2y-3xy+6x^2y+5xy-9x^2y\)

\(=(3x^2y+6x^2y-9x^2y)-3xy+5xy\)

\(=2xy.\)

Thay \(x=\displaystyle\frac{2}{3},\ y=-\displaystyle\frac{3}{4}\) vào biểu thức ta có: \(2.\displaystyle\frac{2}{3}.\left(-\displaystyle\frac{3}{4}\right)=-1.\)

b) \(x(x-2y)-y(y^2-2x)\)

\(=x^2-2xy-y^3+2xy\)

\(=x^2-y^3\)

Thay \(x = 5,\ y = 3\) vào biểu thức ta có: \(5^2-3^3=-2.\)

\(\)

8. Trên một dòng sông, để đi được 10 km, một chiếc xuồng tiêu tốn a lít dầu khi xuôi dòng và tiêu tốn (a + 2) lít dầu khi ngược dòng. Viết biểu thức biểu thị số lít dầu mà xuồng tiêu tốn để đi từ bến A ngược dòng đến bến B, rồi quay lại bến A. Biết khoảng cách giữa hai bến là b km.

Giải

Để đi được \(1\) km, chiếc xuồng tiêu tốn \(\displaystyle\frac{a}{10}\) lít dầu khi xuôi dòng và tiêu tốn \(\displaystyle\frac{a+2}{10}\) lít dầu khi ngược dòng.

Số lít dầu mà chiếc xuồng tiêu tốn để đi từ bến A ngược dòng đến bến B, rồi quay lại bến A là:

\(\displaystyle\frac{a+2}{10}.b+\displaystyle\frac{a}{10}.b\)

\(=\displaystyle\frac{ab}{10}+\displaystyle\frac{2b}{10}+\displaystyle\frac{ab}{10}\)

\(=\displaystyle\frac{2ab}{10}+\displaystyle\frac{b}{5}\)

\(=\displaystyle\frac{ab}{5}+\displaystyle\frac{b}{5}\) (lít dầu).

\(\)

9. a) Tính chiều dài của hình chữ nhật có diện tích bằng \(6xy+10y^2\) và chiều rộng bằng \(2y.\)

b) Tính diện tích đáy của hình hộp chữ nhật có thể tích bằng \(12x^3-3xy^2+9x^2y\) và chiều cao bằng \(3x.\)

Giải

a) Chiều dài của hình chữ nhật là:

\((6xy+10y^2):2y\)

\(=6xy:2y+10y^2:2y\)