Chủ đề 1. Bài 4. Hệ nhị phân và dữ liệu số nguyên

Bài 4 hệ nhị phân và dữ liệu số nguyên trang 20 sách giáo khoa Tin Học lớp 10 – NXB Kết Nối Tri Thức Với Cuộc Sống, mời các em tham khảo cùng Bumbii.

Chủ đề 1. Máy tính và xã hội tri thức. Bài 4. Hệ nhị phân và dữ liệu số nguyên.

HỆ NHỊ PHÂN VÀ BIỂU DIỄN SỐ NGUYÊN

Hoạt động 1. Biểu diễn một số dưới dạng tổng các lũy thừa của 2

Em hãy viết số 19 thành tổng các luỹ thừa của 2.

Gợi ý: Hãy lập danh sách các luỹ thừa của 2 như 16, 8, 4, 2, 1 và tách dần khỏi 19 cho đến hết.

Đáp án:

Kết quả phân tích số 19 = 2⁴ + 2¹ + 2⁰

Hay 19 = 1 x 2⁴ + 0 x 2³ + 0 x 2² + 1 x2¹ + 1 x 2⁰

Câu hỏi

1. Em hãy đổi các số sau từ hệ thập phân sang hệ nhị phân.

a) 13.

b) 155.

c) 76.

Đáp án:

a) 13₁₀ = 1101₂.

b) 155₁₀ = 10011011₂.

c) 76₁₀ = 1001100₂.

2. Em hãy đổi các số sau từ hệ nhị phân sang hệ thập phân.

a) 110011.

b) 10011011.

c) 1001110.

Đáp án:

a) 110011₂ = 51₁₀.

b) 10011011₂ = 155₁₀.

c) 1001110₂ = 78₁₀.

CÁC PHÉP TÍNH SỐ HỌC TRONG HỆ NHỊ PHÂN

Hoạt động 2. Phép tính trong hệ nhị phân

Hãy chuyển các toán hạng của hai phép tính sau ra hệ nhị phân để chuẩn bị kiểm tra kết quả thực hiện các phép toán trong hệ nhị phân. (Ví dụ 3 + 4 = 7 sẽ được chuyển dạng thành 11 + 100 = 111).

a) 27 + 26 = 53.

b) 13 x 5 = 65.

Đáp án:

a) 27 + 26 = 53 -> 11011 + 11010 = 110101.

b) 13 x 5 = 65 -> 1101 x 101 = 1000001.

Câu hỏi

Hãy thực hiện các phép tính sau trong hệ nhị phân:

a) 101101 + 11001.

b) 100111 x 1011.

Đáp án:

a) 101101 + 11001 -> 45 + 25 = 70.

b) 100111 x 1011 -> 39 x 11 = 429.

LUYỆN TẬP

Thực hiện tính toán trên máy tính luôn theo quy trình sau:

Quy trình thực hiện phép tính trên máy tính, hệ nhị phân và dữ liệu số nguyên — Hình 4.4. Quy trình thực hiện phép tính trên máy tính

Câu 1. Hãy thực hiện các phép tính sau đây theo quy trình Hình 4.4.

a) 125 + 17.

b) 250 + 175.

c) 75 + 112.

Đáp án:

a) 125 + 17 -> 1111101 + 10001 = 10001110 -> 142.

b) 250 + 175 -> 11111010 + 10101111 = 110101001 -> 425.

c) 75 + 112 -> 1001011 + 1110000 = 10111011 -> 187.

Câu 2. Em hãy thực hiện các phép tính sau đây theo quy trình Hình 4.4.

a) 15 x 6.

b) 11 x 9.

c) 125 x 4.

Đáp án:

a) 15 x 6 -> 1111 x 110 = 1011010 -> 90.

b) 11 x 9 -> 1011 x 1001 = 1100011 -> 99.

c) 125 x 4 -> 1111101 x 100 = 111110100 -> 500.

VẬN DỤNG

Câu 1. Em hãy tìm hiểu trên Internet hoặc các tài liệu khác cách đổi phần thập phân của một số trong hệ thập phân sang hệ đếm nhị phân.

Đáp án:

Cách đổi phần thập phân của một số sang hệ nhị phân bằng cách nhân 2 và tách phần nguyên liên tiếp qua ví dụ đổi số 0,72.

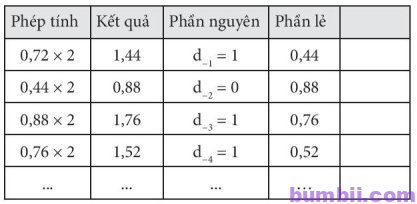
Vậy 0,72₁₀ = 0,1011100…₂

Lưu ý: Quá trình này có thể không bao giờ kết thúc. Chúng ta sẽ phải dừng ở một bước nào đó và chịu một sai số làm trò.

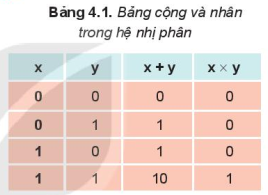
Phép cộng, phép nhân hai số nhị phân được thực hiện tương tự trong hệ thập phân, thực hiện từ phải sang trái.

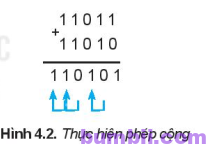
Khi phép cộng hai bit có kết quả là 10 thì ghi 0 ở hàng tương ứng dưới tổng và nhớ 1 sang hàng bên trái. Có thể xảy ra trường hợp cộng hai bit 1 mà phải nhớ 1 từ hàng trước chuyển sang thì kết quả sẽ là 11, khi đó chúng ta ghi 1 ở hàng tương ứng dưới tổng và nhớ 1 sang hàng tiếp theo bên trái. Hình 4.2.

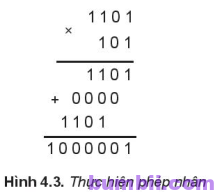
Ta sẽ nhân thừa số thứ nhất lần lượt với từng chữ số của thừa số thứ hai, theo thứ tự từ phải sang trái và đặt kết quả căn phải theo đúng vị trí chữ số của thừa số thứ hai, rồi cộng tất cả lại. Hình 4.3.

Câu 2. Em hãy tìm hiểu mã bù 2 với hai nội dung:

a) Mã bù 2 được lập như thế nào?

b) Mã bù 2 được dùng để làm gì?

Đáp án:

Đối với số nguyên có dấu, có một số cách mã hoá như mã thuận (còn gọi là mã dấu – lượng), mã bù 1 (còn gọi là mã đảo) và mã bù 2.

Mã bù 2 là một số trong hệ nhị phân là bù đúng của một số khác. Số biểu diễn ở dạng bù 2 là số biểu diễn ở bù 1 rồi sau đó cộng thêm 1.

Ví dụ: số nguyên -7 ở hệ thập phân được biểu diễn trong máy tính theo dạng mã bù 2 như sau:

Bước 1: xác định số nguyên -7 ở hệ thập phân: 1000 0111.

Bước 2: biểu diễn dạng mã bù 1 (đảo tất cả các bit ở bước 1). Vì biểu diễn số âm nên không đảo bit dấu (-) là bit 1 ở vị trí đầu bên trái. Kết quả là: 1111 1000.