Chương 8 – Bài 7: Tính chất ba đường trung tuyến của tam giác trang 75 sách giáo khoa toán lớp 7 tập 2 NXB Chân Trời Sáng Tạo.
\(1.\) Quan sát Hình \(8\). Thay \(\fbox{?}\) bằng số thích hợp.
\(EG = \fbox{?}\ EM;\hspace{2cm} GM = \fbox{?}\ EM;\)
\(GM = \fbox{?}\ EG; \hspace{2cm} FG = \fbox{?}\ GN;\)
\(FN = \fbox{?}\ GN;\hspace{2cm} FN = \fbox{?}\ FG.\)
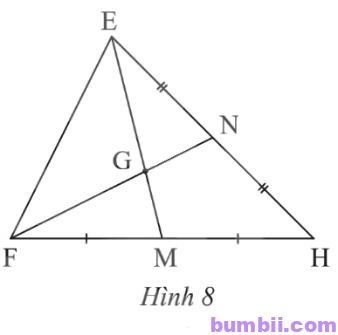
Giải
Ta có G là giao điểm hai đường trung tuyến của tam giác EFH do đó G là trọng tâm của tam giác EFH nên:
\(EG = \displaystyle\frac{2}{3} EM;\hspace{2cm} GM = \displaystyle\frac{1}{3} EM;\)
\(GM = \displaystyle\frac{1}{2} EG; \hspace{2cm} FG = 2 GN;\)
\(FN = 3 GN;\hspace{2cm} FN = \displaystyle\frac{3}{2} FG.\)
\(\)
\(2.\) Quan sát Hình \(9\).
a) Biết AM = \(15\) cm, tính AG.
b) Biết GN = \(6\) cm, tính CN.
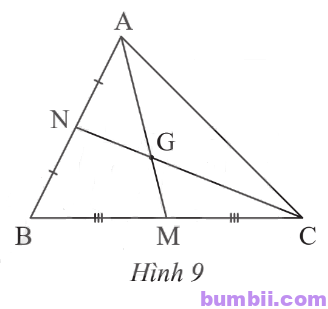
Giải
a) G là giao điểm hai đường trung tuyến của \(\Delta ABC\) nên G là trọng tâm của \(\Delta ABC\).
Do đó \(AG = \displaystyle\frac{2}{3}.AM = \displaystyle\frac{2}{3}\ .\ 15 = 10\) cm.
b) Do G là trọng tâm của tam giác ABC nên \(GN = \displaystyle\frac{1}{3}CN\).
Do đó \(CN = 3GN = 3\ .\ 6 = 18\) cm.
\(\)
\(3.\) Cho tam giác ABC. Hai đường trung tuyến AM và CN cắt nhau tại G. Trên tia đối của tia MA lấy điểm E sao cho ME = MG.
a) Chứng minh rằng BG song song với EC.
b) Gọi I là giao điểm của BM và CN, đường thẳng AI cắt BC tại H. Chứng minh H là trung điểm của BC.
Giải
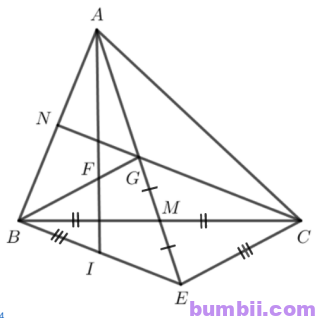
a) Do AM là đường trung tuyến của \(\Delta ABC\) nên M là trung điểm của BC.
=> BM = CM.
Xét \(\Delta BMG\) và \(\Delta CME\) có:
BM = CM (chứng minh trên).
\(\widehat{BMG} =\widehat{CME}\) (đối đỉnh).
MG = ME (giả thiết).
Do đó \(\Delta BMG=\Delta CME\) (c.g.c).
Suy ra \(\widehat{BGM} =\widehat{CEM}\).
Mà hai góc này ở vị trí so le trong nên BG // EC.
b) Do G là trọng tâm của \(\Delta ABC\) nên \(AG = 2GM\).
Lại có ME = GM và G, M, E thẳng hàng nên \(GE = GM + ME = 2GM\).
Suy ra AG = GE.
Do đó G là trung điểm của AE.
Tam giác ABE có hai đường trung tuyến AI và BG cắt nhau tại F nên F là trọng tâm của tam giác ABE.
Do đó AF = 2FI.
\(4.\) Cho tam giác ABC cân tại A có BM và CN là hai đường trung tuyến.
a) Chứng minh rằng BM = CN.
b) Gọi I là giao điểm của BM và CN, đường thẳng AI cắt BC tại H. Chứng minh H là trung điểm của BC.
Giải
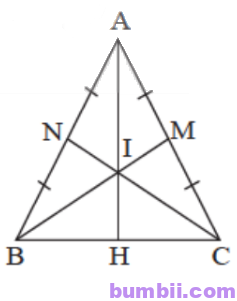
a) N là trung điểm của AB => AN = NB = \(\displaystyle\frac{1}{2}\) AB
M là trung điểm của AC => AM = MC = \(\displaystyle\frac{1}{2}\) AC
=> AN = AM
Xét \(\Delta ANC\) và \(\Delta AMB\) ta có:
AB = AC (\(\Delta ABC\) cân tại A)
\(\widehat{A}\) là góc chung
AN = AM
=> \(\Delta ANC=\Delta AMB\) (c.g.c).
=> NC = MB (hai cạnh tương ứng).
b) Tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại I nên I là trọng tâm của tam giác ABC.
Khi đó AI đi qua trung điểm của BC.
Mà AI cắt BC tại H nên H là trung điểm của BC.
\(\)
\(5.\) Cho tam giác ABC có đường trung tuyến BM bằng trung tuyến CN. Chứng minh rằng tam giác ABC cân.
Giải
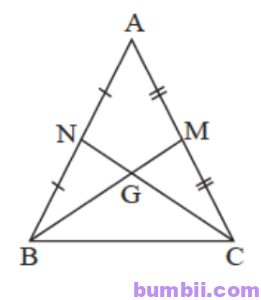
Gọi G là trọng tâm của tam giác ABC (G là giao điểm của hai đường trung tuyến BM và CN).
\(BG = \displaystyle\frac{2}{3}BM,\ GM = \displaystyle\frac{1}{3}BM,\ CG = \displaystyle\frac{2}{3}CN,\ GN = \displaystyle\frac{1}{3}CN\).
Mà BM = CN nên BG = CG, GM = GN.
Xét \(\Delta BGN\) và \(\Delta CGM\) có:
GM = GN (chứng minh trên).
\(\widehat{NIB} =\widehat{MIC}\) (đối đỉnh).
BG = CG (chứng minh trên).
Do đó \(\Delta BGN=\Delta CGM\) (c.g.c).
Suy ra BN = CM.
Do BM và CN là các đường trung tuyến của tam giác ABC nên M và N lần lượt là trung điểm của AC và AB.
Suy ra BN = \(\displaystyle\frac{1}{2}\)AB, CM = \(\displaystyle\frac{1}{2}\)AC.
Do đó AB = AC.
Tam giác ABC có AB = AC nên tam giác ABC cân tại A.
\(\)
\(6.\) Cho tam giác ABC cân tại A có BE và CD là hai đường trung tuyến cắt nhau tại F (Hình \(10\)). Biết BE = \(9\) cm, tính độ dài đoạn thẳng DF.
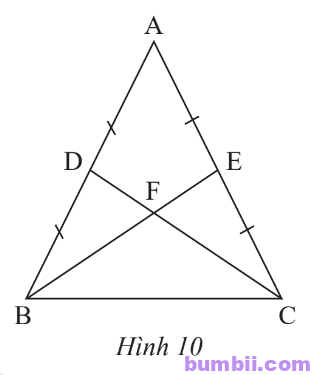
Giải
D là trung điểm của AB => AD = DB = \(\displaystyle\frac{1}{2}\) AB.
E là trung điểm của AC => AE = EC = \(\displaystyle\frac{1}{2}\) AC.
Xét \(\Delta BCD\) và \(\Delta CBE\) ta có:
\(\widehat{DBC} = \widehat{ECB}\) (\(\Delta ABC\) cân tại A)
BC là cạnh chung
DB = EC (chứng minh trên)
=> \(\Delta BCD=\Delta CBE\) (c.g.c).
Suy ra CD = BE = \(9\) cm.
F là trọng tâm tam giác ABC, suy ra DF = \(\displaystyle\frac{1}{3}\)CD = \(3\) cm.
\(\)
Xem bài giải trước: Bài 6: Tính chất ba đường trung trực của tam giác
Xem bài giải tiếp theo: Bài 8: Tính chất ba đường cao của tam giác
Xem thêm các bài giải khác tại: Giải bài tập SGK Toán Lớp 7 – NXB Chân Trời Sáng Tạo.
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech
