Ôn tập chương VIII

Ôn tập chương VIII trang 44 sách bài tập toán lớp 7 tập 2 NXB Kết nối tri thức với cuộc sống.

A CÂU HỎI (Trắc nghiệm)

1. Biến cố “Nhiệt độ cao nhất trong tháng Sáu năm sau tại Thành phố Hồ Chí Minh là \(10^oC\)” là

A. Biến cố chắc chắn

B. Biến cố ngẫu nhiên

C. Biến cố không thể

D. Biến cố đồng khả năng

Giải

Biến cố “Nhiệt độ cao nhất trong tháng Sáu năm sau tại Thành phố Hồ Chí Minh là \(10^oC\)” là biến cố không thể vì nhiệt độ tháng Sáu (mùa hè) luôn cao hơn \(10^oC.\)

Chọn đáp án C.

\(\)

2. Biến cố “Ngày mai có mưa rào và giông ở Hà Nội” là:

A. Biến cố ngẫu nhiên

B. Biến cố chắc chắn

C. Biến cố đồng khả năng

D. Biến cố không thể

Giải

Biến cố “Ngày mai có mưa rào và giông ở Hà Nội” là biến cố ngẫu nhiên vì điều này không chắc có thể xảy ra.

Chọn đáp án A.

\(\)

3. Hai túi I và II chứa các tấm thẻ được ghi số 3; 4; 5; 6; 7. Từ mỗi túi rút ngẫu nhiên một tấm thẻ.

a) Xác suất của biến cố “Tích hai số ghi trên hai tấm thẻ lớn hơn 8” bằng

A. \(0\) \(\hspace{2cm}\) B. \(\displaystyle\frac{1}{2}\)

C. \(1\) \(\hspace{2cm}\) D. \(0,25\)

b) Xác xuất của biến cố “Tổng hai số ghi trên hai tấm thẻ nhỏ hơn 5” bằng

A. \(1 \hspace{2cm}\) B. \(0\)

C. \(0,45 \hspace{1,5cm}\) D. \(0,5\)

c) Biến cố “Hiệu hai số ghi trên hai tấm thẻ là số chẵn” là

A. Biến cố ngẫu nhiên

B. Biến cố chắc chắn

C. Biến cố không thể

D. Biến cố đồng khả năng

Giải

a) Tích của hai số trên hai tấm thẻ nhỏ nhất là: 3 . 4 = 12 nên biến cố “Tích hai số ghi trên hai tấm thẻ lớn hơn 8” là biến cố chắc chắn, xác xuất bằng 1.

Chọn đáp án C.

b) Tổng của hai số trên hai tấm thẻ nhỏ nhất là: 3 + 4 = 7 nên biến cố “Tổng hai số ghi trên hai tấm thẻ nhỏ hơn 5” là biến cố không thể, xác xuất bằng 0.

Chọn đáp án B.

c) Biến cố “Hiệu hai số ghi trên hai tấm thẻ là số chẵn” là biến cố ngẫu nhiên vì điều này không chắc có thể xảy ra. (Ví dụ hiệu của hai số 4 và 3 là 1).

Chọn đáp án A.

\(\)

4. Một thùng kín có 20 quả bóng màu đỏ và 20 quả bóng màu xanh. Sơn lấy ngẫu nhiên một quả bóng trong thùng.

a) Xác suất của biến cố “Lấy được quả bóng màu xanh” bằng

A. \(1\) \(\hspace{2cm}\) B. \(\displaystyle\frac{1}{2}\)

C. \(0\) \(\hspace{2cm}\) D. \(0,8\)

b) Xác suất của biến cố “Lấy được quả bóng màu đỏ” bằng

A. \(0 \hspace{2cm}\) B. \(1\)

C. \(0,5 \hspace{1,5cm}\) D. \(0,2\)

c) Xác suất của biến cố “Lấy được quả bóng màu đỏ hoặc màu xanh” bằng

A. \(1 \hspace{2cm}\) B. \(0\)

C. \(0,5 \hspace{1,5cm}\) D. \(0,4\)

Giải

a) Biến cố “Lấy được quả bóng màu xanh” và biến cố “Lấy được quả bóng màu đỏ” là đồng khả năng vì số bóng xanh bằng với số bóng đỏ. Vậy xác suất của biến cố “Lấy được quả bóng màu xanh” là \(\displaystyle\frac{1}{2}.\)

Chọn đáp án B.

b) Biến cố “Lấy được quả bóng màu đỏ” và biến cố “Lấy được quả bóng màu xanh” là đồng khả năng vì số bóng đỏ bằng với số bóng xanh. Vậy xác suất của biến cố cố “Lấy được quả bóng màu đỏ” là 0,5.

Chọn đáp án C.

c) Trong tất cả những quả bóng ở trong thùng chỉ có hai màu đỏ và xanh. Do đó biến cố “Lấy được quả bóng màu đỏ hoặc màu xanh” là biến cố chắc chắn. Vậy xác suất của biến cố đã cho bằng 1.

Chọn đáp án A.

\(\)

B BÀI TẬP

8.10. Một bài thi trắc nghiệm có 18 câu hỏi được đánh số từ 1 đến 18. Chọn ngẫu nhiên một câu hỏi trong bài thi.

a) Xét hai biến cố sau:

A: “Số thứ tự của câu hỏi được chọn là số có một chữ số”;

B: “Số thứ tự của câu hỏi được chọn là số có hai chữ số”.

Hai biến cố A và B có đồng khả năng không? Tại sao?

b) Tính xác suất của hai biến cố A và B.

Giải

a) Hai biến cố A và B đồng khả năng vì số lượng câu hỏi mang số thứ tự là số có một chữ số bằng số lượng câu hỏi mang số thứ tự là số có hai chữ số và đều bằng 9 câu.

b) Biến cố A và B đồng khả năng. Do đó xác suất của biến cố A và B bằng nhau và đều bằng \(\displaystyle\frac{1}{2}.\)

\(\)

8.11. Một tấm bài cứng hình tròn được chia làm tám phần có diện tích bằng nhau và ghi các số 1; 2; 3; 4; 5; 6; 7; 8; được gắn vào trục quay có mũi tên ở tâm như Hình 8.3.

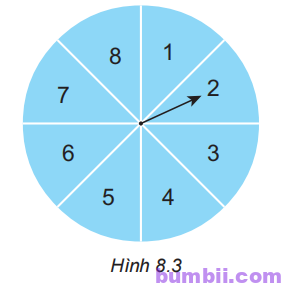
Giải Bài tập Toán Lớp 7 – NXB Kết Nối Tri Thức Với Cuộc Sống

Bạn Hùng quay tấm bìa. Tính xác suất để:

a) Mũi tên dừng ở hình quạt ghi số nhỏ hơn 9;

b) Mũi tên đừng ở hình quạt ghi số 0;

c) Mũi tên dừng ở hình quạt ghi số chẵn;

d) Mũi tên dừng ở hình quạt ghi số 7 hoặc 8.

Giải

a) Xác suất bằng 1 vì đây là biến cố chắc chắn (tất cả các hình quạt đều ghi số nhỏ hơn 9).

b) Xác suất bằng 0 vì đây là biến cố không thể (không có hình quạt nào ghi số 0).

c) Biến cố “Mũi tên dừng ở hình quạt ghi số chẵn” và biến cố “mũi tên dừng ở hình quạt ghi số lẻ” là đồng khả năng.

Vậy xác suất của biến cố cần tìm là \(\displaystyle\frac{1}{2}.\)

d) Xét bốn biến cố sau:

A: “Mũi tên dừng ở hình quạt ghi số 1 hoặc 2”;

B: “Mũi tên dừng ở hình quạt ghi số 3 hoặc 4”;

C: “Mũi tên dừng ở hình quạt ghi số 5 hoặc 6”;

D: “Mũi tên dừng ở hình quạt ghi số 7 hoặc 8”;

Biến cố A xảy ra khi mũi tên dừng ở hình quạt ghi số 1 hoặc số 2.

Biến cố B xảy ra khi mũi tên dừng ở hình quạt ghi số 3 hoặc số 4.

Biến cố C xảy ra khi mũi tên dừng ở hình quạt ghi số 5 hoặc số 6.

Biến cố D xảy ra khi mũi tên dừng ở hình quạt ghi số 7 hoặc số 8.

Vì quay ngẫu nhiên nên mỗi hình quạt có khả năng quay được như nhau.

Do đó bốn biến cố A, B, C, D là đồng khả năng. Vì luôn xảy ra duy nhất một trong bốn biến cố này nên xác suất của biến cố D là \(\displaystyle\frac{1}{4}.\)

Vậy xác suất của biến cố “Lấy được quả cầu ghi số 7 hoặc 8” là \(\displaystyle\frac{1}{4}.\)

\(\)

8.12. Một hộp đựng 14 quả cầu được đánh các số 10; 11; …; 23. Lẫy ngẫu nhiên một quả cầu trong hộp. Tính xác suất để:

a) Quả cầu lấy được ghi số 24;

b) Quả cầu lấy được ghi số lẻ;

c) Quả cầu lấy được ghi số 11;

d) Quả cầu lấy được mang số 12 hoặc 13.

Giải

a) Xác xuất bằng 0 vì đây là biến cố không thể do không có quả cầu nào đánh số 24.

b) Biến cố “Quả cầu lấy được ghi số chẵn” và biến cố “Quả cầu lấy được ghi số lẻ” là đồng khả năng.

Vậy xác suất của biến cố cần tìm là \(\displaystyle\frac{1}{2}.\)

c) Mỗi quả cầu có khả năng lấy được như nhau. Có 14 biến cố đồng khả năng. Vậy xác suất của biến cố đang xét là \(\displaystyle\frac{1}{14}.\)

d) Xét 7 biến cố sau:

A: “Quả cầu lấy được mang số 10 hoặc 11”;

B: “Quả cầu lấy được mang số 12 hoặc 13”;

C: “Quả cầu lấy được mang số 14 hoặc 15”;

D: “Quả cầu lấy được mang số 16 hoặc 17”;

E: “Quả cầu lấy được mang số 18 hoặc 19”;

F: “Quả cầu lấy được mang số 20 hoặc 21”;

G: “Quả cầu lấy được mang số 22 hoặc 23”;

Do lấy ngẫu nhiên nên mỗi quả cầu có khả năng rút được như nhau.

Vậy bảy biến cố A, B, C, D, E, F, G là đồng khả năng. Vì luôn xảy ra duy nhất một trong bảy biến cố này nên xác suất của biến cố B là \(\displaystyle\frac{1}{7}.\)

\(\)

8.13. Một hộp đựng 20 quả bóng có cùng kích thước, khác nhau về màu sắc trong đó có 4 quả bóng màu xanh, 4 quả bóng màu đỏ, 4 quả bóng màu tím, 4 quả bóng màu vàng và 4 quả bóng màu trắng. Bạn Minh lấy ngẫu nhiên một quả bóng từ trong hộp.

Xét 5 biến cố sau:

A: “Minh lấy được quả bóng màu xanh”;

B: “Minh lấy được quả bóng màu đỏ”;

C: “Minh lấy được quả bóng màu tím”;

D: “Minh lấy được quả bóng màu vàng”;

E: “Minh lấy được quả bóng màu trắng”;

a) Hãy giải thích vì sao các biến cố A, B, C, D, E là đồng khả năng.

b) Tính xác suất của các biến cố A, B, C, D, E.

Giải

a) Mỗi quả bóng có khả năng được chọn như nhau. Số quả bóng màu xanh, màu đỏ, màu tím, màu vàng và màu trắng bằng nhau nên các biến cố A, B, C, D, E là đồng khả năng.

b) Vì luôn xảy ra duy nhất một biến cố trong năm biến cố này nên xác suất của năm biến cố bằng nhau và bằng \(\displaystyle\frac{1}{5}.\)

\(\)

8.14. Một thùng kín có 40 quả bóng cùng kích thước, một số quả có màu trắng và một số quả có màu đen. Sơn lấy ngẫu nhiên một quả bóng trong thùng. Biết rằng biến cố “Sơn chọn được quả bóng màu trắng” và biến cố “Sơn chọn được quả bóng màu đen” là đồng khả năng. Hỏi trong thùng chứa bao nhiêu quả bóng màu trắng.

Giải

Biến cố “Sơn chọn được quả bóng màu trắng” và biến cố “Sơn chọn được quả bóng màu đen” là đồng khả năng. Do đó, số quả bóng màu trắng bằng số quả bóng màu đen. Vậy trong thùng chứa 20 quả bóng màu trắng.

\(\)

8.15. Một chuyến xe khách có 28 hành khách nam và 31 hành khách nữ. Đến một bến xe có một số hành khách nữ xuống xe. Chọn ngẫu nhiên một hành khách còn lại trên xe. Biết rằng xác suất để chọn được hành khách nữ là \(\displaystyle\frac{1}{2}.\) Hỏi có bao nhiêu hành khách nữ đã xuống xe?

Giải

Gọi số hành khách nữ xuống xe là n (người). Khi đó, trên xe còn \(31 – n\) hành khách nữ và 28 hành khách nam.

Xác suất để chọn được hành khách nữ là \(\displaystyle\frac{1}{2}\) nên số hành khách nữ còn lại trên xe bằng số hành khách nam. Do đó, \(31-n = 28\) suy ra n = 3.

Vậy có 3 số hành khách nữ đã xuống xe.

\(\)

8.16. Một chiếc hộp chứa 50 viên bi cùng kích thước gồm một số viên bi màu xanh; một số viên bi màu đỏ; một số viên bi màu trắng; một số viên bi màu tím và một số viên bi màu vàng. Bạn Bình lấy ngẫu nhiên một viên bi trong hộp. Biết rằng 5 biến cố sau đây là đồng khả năng:

A: “Bình lấy được viên bi màu xanh”;

B: “Bình lấy được viên bi màu đỏ”;

C: “Bình lấy được viên bi màu trắng”;

D: “Bình lấy được viên bi màu tím”;

E: “Bình lấy được viên bi màu vàng”;

Hỏi trong hộp chứa bao nhiêu viên bi mỗi loại?

Giải

Do lấy ngẫu nhiên nên mỗi viên bi có khả năng được lấy như nhau.

Do đó số viên bi màu xanh, số viên bi màu đỏ, số viên bi màu trắng, số viên bi màu tím và số viên bi màu vàng bằng nhau.

Vậy trong hộp mỗi loại có 10 viên bi.

\(\)

Xem bài giải trước: Bài 30: Làm quen với xác suất của biến cố