Chương 4 – Luyện tập chung trang 69 sách giáo khoa toán lớp 7 tập 1 NXB Kết nối tri thức với cuộc sống.
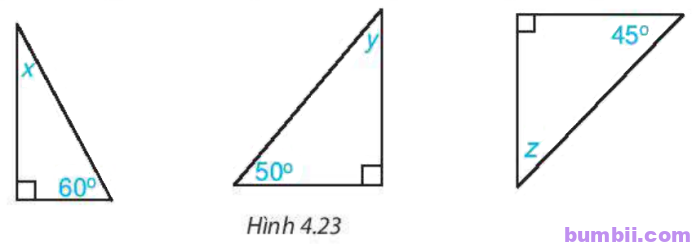
4.7. Các số đo x, y, z trong mỗi tam giác vuông dưới đây bằng bao nhiêu độ?
Giải
a) Ta có \(x+90^o+60^o=180^o\) (tổng ba góc trong một tam giác bẳng \(180^o\)).
Do đó \(x = 180^o-60^o-90^o= 30^o.\)
b) Ta có \(y+90^o+50^o=180^o\) (tổng ba góc trong một tam giác bẳng \(180^o\)).
Do đó \(y = 180^o-50^o-90^o= 40^o.\)
c) Ta có \(z+90^o+45^o=180^o\) (tổng ba góc trong một tam giác bẳng \(180^o\)).
Do đó \(z = 180^o-45^o-90^o= 45^o.\)
\(\)
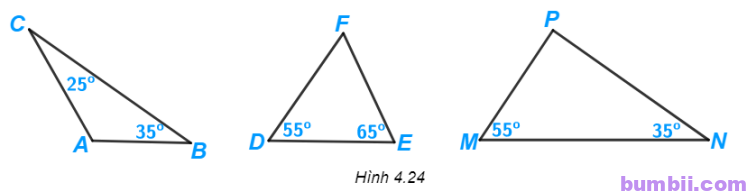
4.8. Tính số đo góc còn lại trong mỗi tam giác dưới đây. Hãy chỉ ra tam giác nào là tam giác vuông.
Giải
Ta có \(\widehat{A} + \widehat{B} + \widehat{C} = 180^o\) (tổng ba góc trong một tam giác bẳng \(180^o\)).
\(\widehat{A} = 180^o-(\widehat{B} + \widehat{C})\) \(= 180^o-(25^o + 35^o) = 120^o.\)
Ta có \(\widehat{D} + \widehat{E} + \widehat F = 180^o\) (tổng ba góc trong một tam giác bẳng \(180^o\)).
\(\widehat F = 180^o-(\widehat{D} + \widehat{E})\) \(= 180^o-(55^o + 65^o) = 60^o.\)
Ta có \(\widehat P + \widehat{M} + \widehat{N} = 180^o\) (tổng ba góc trong một tam giác bẳng \(180^o\)).
\(\widehat P = 180^o-(\widehat{M} + \widehat{N})\) \(= 180^o-(55^o + 35^o) = 90^o.\)
Tam giác PMN là tam giác vuông.
\(\)
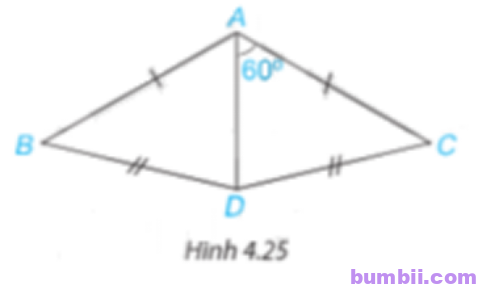
4.9. Cho hình 4.25, biết \(\widehat{DAC} = 60^o, AB = AC; DB = DC\). Hãy tính \(\widehat{DAB}\).
Giải
Hai tam giác ADB và ADC có:
AB = AC (theo giả thiết);
BD = CD (theo giả thiết);
AD là cạnh chung.
Vậy \(\Delta ADB = \Delta ADC\) (c.c.c).
\(\Rightarrow \widehat{DAB} = \widehat{DAC}=60^o\) (hai góc tương ứng).
Vậy \(\widehat{DAB}=60^o.\)
\(\)
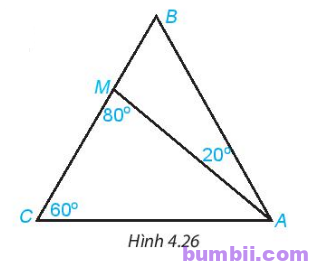
4.10. Cho tam giác ABC có \(\widehat{BCA} =60^o\) và điểm M nằm trên cạnh BC sao cho \(\widehat{BAM} =20^o,\ \widehat{AMC} =80^o\) (H.4.26). Tính số đo các góc AMB, ABC, BAC.
Giải
Trong tam giác AMC có:
\(\widehat{MAC} + \widehat{AMC} + \widehat{C} = 180^o\)
\(\widehat{MAC} = 180^o-\widehat{AMC}-\widehat{C}\)
\(=180^o-80^o-60^o=40^o.\)
Ta có \(\widehat{AMB}\) là góc ngoài tại đỉnh M của tam giác AMC nên
\(\widehat{AMB} = \widehat{ACM} + \widehat{MAC}\) \(= 60^o + 40^o = 100^o.\)
Trong tam giác AMB có:
\(\widehat{AMB} + \widehat{BAM} + \widehat{B} = 180^o\)
\(\widehat{B} = 180^o-\widehat{AMB}-\widehat{BAM}\)
\(\widehat{B}= 180^o-100^o-20^o = 60^o.\)
Hay \(\widehat{ABC} = 60^o.\)
Ta có \(\widehat{BAC} = \widehat{MAB} + \widehat{MAC}\) \(= 20^o + 40^o = 60^o.\)
Vậy \(\widehat{AMB} = 100^o;\ \widehat{ABC} = 60^o;\) \(\widehat{BAC} = 60^o.\)
\(\)
4.11. Cho \(\Delta ABC = \Delta DEF\). Biết rằng \(\widehat{A} = 60^o;\ \widehat{E} = 80^o\), tính số đo các góc B, C, D, F.
Giải
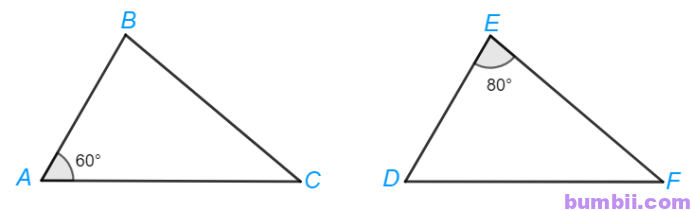
Do \(\Delta ABC=\Delta DEF\) nên:
\(\widehat{D}=\widehat{A}=60^o.\)
\(\widehat{B}=\widehat{E}=80^o.\)
Trong tam giác ABC có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(⇒\widehat{C}=180^o-\widehat{A}-\widehat{B}\)
\(⇒\widehat{C}=180^o-60^o-80^o=40^o.\)
Do \(\Delta ABC=\Delta DEF\) nên:
\(\widehat{C}=\widehat{F}=40^o\) (hai góc tương ứng)
Vậy \(\widehat{B}=80^o,\ \widehat{C}=40^o,\ \widehat{D}=60^o,\ \widehat{F}=40^o.\)
\(\)
Xem bài giải trước: Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác
Xem bài giải tiếp theo: Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác
Xem thêm các bài giải khác tại: Giải Bài tập SGK Toán Lớp 7 – NXB Kết Nối Tri Thức Với Cuộc Sống
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech
