Bài tập cuối chương VI trang 68 sách giáo khoa toán lớp 7 tập 2 NXB Cánh Diều. Các em cùng Bumbii giải các bài tập sau.
1. Biểu thức nào sau đây là đa thức một biến? Tìm biến và bậc của đa thức đó.
a) \(-7x + 5;\)
b) \(2\ 021x^2-2\ 022x + 2\ 023;\)
c) \(2y^3-\displaystyle\frac{3}{y-2}+4;\)
d) \(-2t^m + 8t^2 + t-1,\) với \(m\) là số tự nhiên lớn hơn \(2.\)
Giải
a) Biểu thức \(-7x + 5\) là đa thức một biến \(x,\) đa thức này có bậc bằng \(1.\)
b) Biểu thức \(2\ 021x^2-2\ 022x + 2\ 023\) là đa thức một biến \(x,\) đa thức này có bậc bằng \(2.\)
c) Biểu thức \(2y^3-\displaystyle\frac{3}{y-2}+4\) không phải là đa thức.
d) Biểu thức \(-2t^m + 8t^2 + t-1\) là đa thức một biến \(t,\) đa thức này có bậc bằng \(m,\) với \(m\) là số tự nhiên lớn hơn \(2.\)
\(\)
2. Tính giá trị của biểu thức:
a) \(A =-5a-b-20\) tại \(a =-4,\ b = 18;\)
b) \(B =-8xyz + 2xy + 16y\) tại \(x =-1,\ y = 3,\ z =-2;\)
c) \(C =-x^{2021}y^2 + 9x^{2021}\) tại \(x =-1,\ y =-3.\)
Giải
a) Thay \(a =-4,\ b = 18\) vào biểu thức \(A =-5a-b-20\) ta có:
\(A = -5.(-4)-18-20\)
\(A = 20-18-20\)
\(A = -18.\)
b) Thay \(x =-1,\ y = 3,\ z =-2\) vào biểu thức \(B =-8xyz + 2xy + 16y\) ta có:
\(B = -8.(-1).3.(-2) + 2.(-1).3 + 16.3\)
\(B = -48 + (-6) + 48\)
\(B = -6.\)
c) Thay \(x =-1,\ y =-3\) vào biểu thức \(C =-x^{2021}y^2 + 9x^{2021}\) ta có:
\(C = -(-1)^2021 .(-3)^2 + 9.(-1)^2021 \)
\(C = -(-1) . 9 + 9 . (-1)\)
\(C = 1.9 + (‒9)\)
\(C = 9 + (-9)\)
\(C = 0.\)
\(\)
3. Viết đa thức trong mỗi trường hợp sau:
a) Đa thức bậc nhất có hệ số của biến bằng -2 và hệ số tự do bằng 6;
b) Đa thức bậc hai có hệ số tự do bằng 4;
c) Đa thức bậc bốn có hệ số của lũy thừa bậc 3 của biến bằng 0;
d) Đa thức bậc sáu trong đó tất cả hệ số của lũy thừa bậc lẻ của biến đều bằng 0.
Giải
a) Đa thức bậc nhất có hệ số của biến bằng \(-2\) và hệ số tự do bằng \(6:\) \(-2x +6.\)
b) Đa thức bậc hai có hệ số tự do bằng \(4\) có dạng: \(ax^2 + bx + 4\) với \(a,\ b ∈ \mathbb{R}\) và \(a ≠ 0.\)
Ví dụ: \(x^2+4,\) \(-3x^2-x+4,…\)
c) Đa thức bậc bốn có hệ số của lũy thừa bậc \(3\) của biến bằng \(0\) có dạng: \(ax^4 + bx^2 + cx + d\) với \(a,\ b,\ c,\ d ∈ \mathbb{R}\) và \(a ≠ 0.\)
Ví dụ: \(x^4,\) \(-x^4+x^2+1,…\)
d) Đa thức bậc sáu trong đó tất cả hệ số của lũy thừa bậc lẻ của biến đều bằng \(0\) có dạng \(ax^6 + bx^4 + cx^2 + d\) với \(a,\ b,\ c,\ d ∈ \mathbb{R}\) và \(a ≠ 0.\)
Ví dụ: \(x^6+x^4+x^2+1,\) \(x^6+5,…\)
\(\)
4. Kiểm tra xem trong các số -1, 0, 1, 2, số nào là nghiệm của mỗi đa thức sau:
a) \(3x-6;\)
b) \(x-1;\)
c) \(3x^2-4x;\)
d) \(x^2 + 9.\)
Giải
a) Thay các giá trị \(-1,\ 0,\ 1,\ 2\) vào đa thức ta có:
\(3.(-1)-6=-3-6=-9 ≠ 0.\)
\(3.0-6=0-6=-6 ≠ 0.\)
\(3.1-6=3-6=-3 ≠ 0.\)
\(3.2-6=6-6=0.\)
Vậy \(x=2\) là nghiệm của đa thức \(3x-6.\)
b) Thay các giá trị \(-1,\ 0,\ 1,\ 2\) vào đa thức ta có:
\((-1)^4-1=1-1=0.\)
\(0^4-1=0-1=-1 ≠ 0.\)
\(1^4-1=1-1=0.\)
\(2^4-1=16-1=15 ≠ 0.\)
Vậy \(x=1\) và \(x=-1\) là nghiệm của đa thức \(x-1.\)
c) Thay các giá trị \(-1,\ 0,\ 1,\ 2\) vào đa thức ta có:
\(3.(-1)^2-4.(-1)=3+4=7 ≠ 0.\)
\(3.0^2-4.0=0-0=0\)
\(3.1^2-4.1=3-4=-1 ≠ 0.\)
\(3.2^2-4.2=12-8=4 ≠ 0.\)
Vậy \(x=0\) là nghiệm của đa thức \(3x^2-4x.\)
d) Thay các giá trị \(-1,\ 0,\ 1,\ 2\) vào đa thức ta có:
\((-1)^2+9=1+9=10≠ 0.\)
\(0^2+9=0+9=9≠ 0.\)
\(1^2+9=1+910≠ 0.\)
\(2^2+9=4+9=13≠ 0.\)
Vậy không giá trị nào là nghiệm của đa thức \(x^2+9.\)
\(\)
5. Cho đa thức \(P(x) = -9x^6 + 4x + 3x^5 + 5x + 9x^6-1.\)
a) Thu gọn đa thức P(x).
b) Tìm bậc của đa thức P(x).
c) Tính giá trị của đa thức P(x) tại \(x = -1;\) \(x = 0;\) \(x = 1.\)
Giải
a) \(P(x) = -9x^6 + 4x + 3x^5 + 5x + 9x^6-1\)
\(= (-9x^6 + 9x^6) + 3x^5 + (4x + 5x)-1\)
\(= 3x^5 + 9x-1.\)
b) Đa thức P(x) có số mũ cao nhất của biến là 5 nên bậc của đa thức P(x) bằng 5.
c) Thay \(x = -1,\) \(x = 0,\) \(x = 1\) vào đa thức \(P(x)= 3x^5 + 9x-1\) ta có:
\(P(-1) = 3.(-1)^5 + 9.(-1)-1\)
\(= 3.(-1) + (-9)-1\)
\(= -3-9-1 =-13.\)
\(P(0) = 3.0^5 + 9.0-1\)
\(= 0 + 0 -1 = -1.\)
\(P(1) = 3.1^5 + 9.1-1\)
\(= 3 + 9-1 = 11.\)
\(\)
6. Tính:
a) \(-2x^2 + 6x^2;\)
b) \(4x^3-8x^3;\)
c) \(3x^4(-6x^2);\)
d) \((-24x^6) : (-4x^3).\)
Giải
a) \(-2x^2 + 6x^2 = (-2 + 6).x^2 = 4x^2.\)
b) \(4x^3-8x^3 = (4-8).x^3 = -4x^3.\)
c) \(3x^4(-6x^2) = 3.(-6).x^4.x^2 = -18x^{4+2} = -18x^6.\)
d) \((-24x^6) : (-4x^3) = [-24 : (-4)].(x^6 : x^3) = 6x^{6-3} = 6x^3.\)
\(\)
7. Tính:
a) \((x^2 + 2x + 3) + (3x^2-5x + 1);\)
b) \((4x^3-2x^2-6)-(x^3-7x^2 + x-5);\)
c) \(-3x^2(6x^2-8x + 1);\)
d) \((4x^2 + 2x + 1)(2x-1);\)
e) \((x^6-2x^4 + x^2) : (-2x^2);\)
g) \((x^5-x^4-2x^3) : (x^2 + x).\)
Giải
a) \((x^2 + 2x + 3) + (3x^2 – 5x + 1)\)
\(= x^2 + 2x + 3 + 3x^2 – 5x + 1\)
\(= (x^2 + 3x^2) + (2x – 5x) + (3 + 1)\)
\(= 4x^2 – 3x + 4.\)
b) \((4x^3 – 2x^2 – 6) – (x^3 – 7x^2 + x – 5)\)
\(= 4x^3 – 2x^2 – 6 – x^3 + 7x^2 – x + 5\)
\(= (4x^3 – x^3) + (-2x^2 + 7x^2) – x + (-6 + 5)\)
\(= 3x^3 + 5x^2 – x – 1.\)
c) \(-3x^2(6x^2 – 8x + 1)\)
\(= -3x^2.6x^2 – (-3x^2).8x + (-3x^2).1\)
\(= – 18x^4 + 24x^3 – 3x^2.\)
d) \((4x^2 + 2x + 1)(2x – 1)\)
\(= 4x^2.2x – 4x^2.1 + 2x.2x – 2x.1 + 1.2x – 1.1\)
\(= 8x^3 – 4x^2 + 4x^2 – 2x + 2x – 1\)
\(= 8x^3 – 1.\)
e) \((x^6 – 2x^4 + x^2) : (-2x^2)\)
\(= x^6 : (-2x^2) – 2x^4 : (-2x^2) + x^2 : (-2x^2)\)
\(=\frac{-1}{2}x^4+x^2-\frac{1}{2}x^0\)
\(=\frac{-1}{2}x^4+x^2-\frac{1}{2}.\)
g) Thực hiện phép chia đa thức ta được:
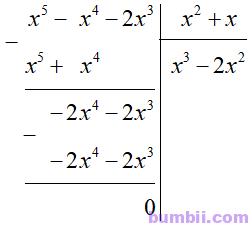
Vậy \((x^5 – x^4 – 2x^3) : (x^2 + x) = x^3 – 2x^2.\)
\(\)
8. Cho hai đa thức: \(A(x) = 4x^4 + 6x^2 – 7x^3 – 5x – 6\) và \(B(x) = -5x^2 + 7x^3 + 5x + 4 – 4x^4.\)
a) Tìm đa thức \(M(x)\) sao cho \(M(x) = A(x) + B(x).\)
b) Tìm đa thức \(C(x)\) sao cho \(A(x) = B(x) + C(x).\)
Giải
a) \(M(x) = A(x) + B(x)\)
\(= (4x^4 + 6x^2 – 7x^3 – 5x – 6) + (-5x^2 + 7x^3 + 5x + 4 – 4x^4)\)
\(= 4x^4 + 6x^2 – 7x^3 – 5x – 6 – 5x^2 + 7x^3 + 5x + 4 – 4x^4\)
\(= (4x^4 – 4x^4) + (-7x^3 + 7x^3) + (6x^2 – 5x^2) + (-5x + 5x) + (-6 + 4)\)
\(= x^2 – 2.\)
b) \(A(x) = B(x) + C(x)\)
Suy ra \(C(x) = A(x) – B(x)\)
\(= (4x^4 + 6x^2 – 7x^3 – 5x – 6) – (-5x^2 + 7x^3 + 5x + 4 – 4x^4)\)
\(= 4x^4 + 6x^2 – 7x^3 – 5x – 6 + 5x^2 – 7x^3 – 5x – 4 + 4x^4\)
\(= (4x^4 + 4x^4) + (-7x^3 – 7x^3) + (6x^2 + 5x^2) + (-5x – 5x) + (-6 – 4)\)
\(= 8x^4 – 14x^3 + 11x^2 – 10x – 10.\)
\(\)
9. Cho \(P(x) = x^3 + x^2 + x + 1\) và \(Q(x) = x^4 – 1.\) Tìm đa thức A(x) sao cho P(x).A(x) = Q(x).
Giải
P(x).A(x) = Q(x)
Suy ra A(x) = Q(x) : P(x).
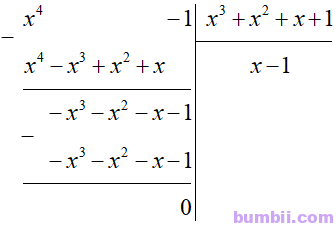
Vậy A(x) = x – 1.
\(\)
10. Nhân dịp lễ Giáng sinh, một cửa hàng bán quần áo trẻ em thông báo khi mua mỗi bộ quần áo sẽ được giảm giá 30% so với giá niêm yết. Giả sử giá niêm yết một bộ quần áo là x (đồng). Viết biểu thức tính số tiền phải trả khi mua loại quần áo đó với số lượng:
a) 1 bộ;
b) 3 bộ;
c) y bộ.
Giải
a) Số tiền phải trả khi mua một bộ quần áo sau khi giảm 30% là:
\((100\%-30\%).x=70\%.x=0,7x\) (đồng).
b) Số tiền phải trả khi mua ba bộ quần áo sau khi giảm 30% là:
\(3.0,7x=\frac{21}{10}x\) (đồng).
c) Số tiền phải trả khi mua \(y\) bộ quần áo sau khi giảm 30% là:
\(y.0,7x=0,7xy\) (đồng).
\(\)
11. Một doanh nghiệp kinh doanh cà phê cho biết: Sau khi rang xong, khối lượng cà phê giảm 12% so với trước khi rang.
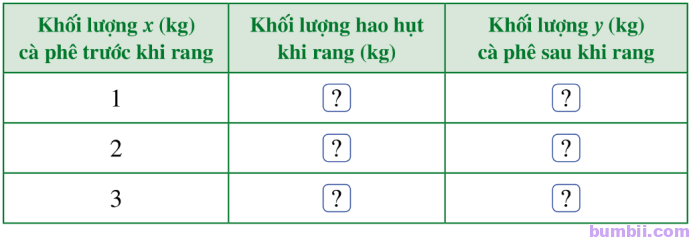
a) Tìm số thích hợp cho \(\fbox{ ? }\) ở bảng sau:
b) Tìm công thức chỉ mối liên hệ giữa x và y.
c) Để có được 2 tấn cà phê sau khi rang thì doanh nghiệp đó cần sử dụng bao nhiêu tấn cà phê trước khi rang?
Giải
a) Ta có bảng sau:
| Khối lượng x (kg) cà phê trước khi rang | Khối lượng hao hụt khi rang (kg) | Khối lượng y (kg) cà phê sau khi rang |
| 1 | 0,12 | 0,88 |
| 2 | 0,24 | 1,76 |
| 3 | 0,36 | 2,64 |
b) Công thức chỉ mối liên hệ giữa x và y:
\(y=x – 12\%.x=x – 0,12x=0,88x.\)
c) Để có được \(2\) tấn cà phê sau khi rang thì doanh nghiệp cần sử dụng số tấn cà phê trước khi rang là:
\(2=0,88x\)
\(x=2:0,88=2,27.\)
Vậy doanh nghiệp cần sử dụng khoảng \(2,27\) tấn cà phê trước khi rang.
\(\)
12. Một công ty sau khi tăng giá 50 nghìn đồng mỗi sản phẩm so với giá ban đầu là \(x\) (nghìn đồng) với \(x < 60\) thì có doanh thu là \(-5x^2 + 50x + 15\ 000\) (nghìn đồng). Tính số sản phẩm mà công ty đã bán được theo \(x.\)
Giải
Giá của sản phẩm sau khi tăng giá là: \(x+50\) (nghìn đồng).
Số sản phẩm mà công ty bán được sau khi tăng giá là:
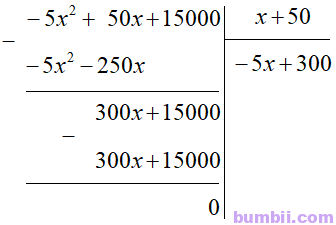
Vậy số sản phẩm mà công ty đã bán được theo x là: \(-5x+300\) (sản phẩm).
\(\)
13. Một công ty du lịch dự định dùng 2 xe ô tô để chở khách đi tham quan, mỗi xe chở tối đa 35 khách, mức giá cho chuyến đi là 900 nghìn/người và đã có 50 người đăng kí tham quan. Công ty đặt chính sách khuyến mãi như sau: Sẽ giảm giá cho mỗi người trong đoàn tham quan là 10 nghìn đồng khi cứ có thêm 1 khách tham quan ngoài 50 khách trên.
a) Giả sử số khách tham quan thêm là x (x ≤ 20). Tính số tiền mà công ty thu được theo x.
b) Nếu 2 xe ô tô của công ty đều chở tối đa số khách thì số tiền công ty thu được tổng cộng là bao nhiêu?
Giải
a) Công ty sẽ giảm giá cho mỗi người 10 nghìn đồng khi cứ có thêm 1 khách tham gia ngoài 50 khách trên. Vậy số tiền mà công ty thu được theo x là:
\((400\ 000-10\ 000x).(50+x)\) (đồng).
b) Số tiền công ty thu được chỉ với 50 khách ban đầu là:
\(50.400\ 000=20\ 000\ 000\) (đồng).
Số tiền công ty thu được sau khi thêm 10 người là:
\((400\ 000-10\ 000.10).(50+10)=390\ 000.60=18000000\) (đồng).
Ta thấy: \(18\ 000\ 000 < 20\ 000\ 000\) nên nếu số khách tăng thêm là 10 người thì số tiền công ty thu được là giảm so với số tiền thu được chỉ với 50 khách ban đầu
\(\)
Xem bài giải trước: Bài 5: Phép chia đa thức một biến
Xem bài giải tiếp theo: Bài 1: Tổng các góc của một tam giác
Xem thêm các bài giải khác tại: Giải bài tập SGK Toán Lớp 7 Cánh Diều
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech
