Bài tập cuối chương 3 trang 66 sách giáo khoa toán lớp 7 tập 1 NXB Chân Trời Sáng Tạo.
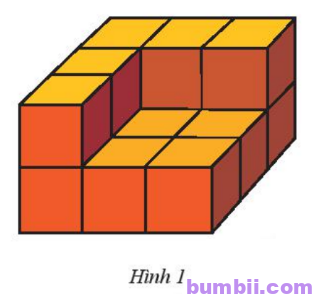
\(1.\) Một hình khối gồm \(14\) hình lập phương gắn kết với nhau như Hình \(1\). Mỗi hình lập phương có cạnh \(1\) cm. Hãy tính thể tích của hình khối này.
Giải
Thể tích của một hình lập phương là: \(1^3 = 1\ (cm^3)\).
Thể tích của khối hình là: \(3.3.2-2.2.1 = 14\ (cm^3)\).
Vậy thể tích của khối hình là \(14\ cm^3\).
\(\)
\(2.\) Một bể cá hình hộp chữ nhật với kích thước mặt đáy là \(5\) dm và \(12\) dm, có mực nước là \(7\) dm. Người ta đổ vào đó một lượng cát (có độ thấm nước không đáng kể) thì thấy mực nước dâng thêm \(1,5\) dm và ngập cát đổ vào. Tính thể tích của lượng cát.
Giải
Thể tích của lượng cát là: \(V=5\ .\ 12\ .\ 1,5=90\ (dm^3)\).
Vậy thể tích cát cho vào bể là \(90\ dm^3\).
\(\)
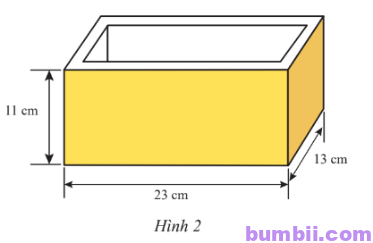
\(3.\) Một khuôn đúc bê tông có kích thước như Hình \(2\). Bể dày các mặt bên của khuôn là \(1,2\) cm. Bề dày mặt đáy của khuôn là \(1,9\) cm. Thể tích của khối bê tông được khuôn này đúc ra là bao nhiêu xăngtimét khối?
Giải
Chiều rộng của mặt đáy khối bê tông được đúc ra là \(13\ – 1,2\ – 1,2 = 10,6\) (cm).
Chiều dài của mặt đáy khối bê tông được đúc ra là \(23\ – 1,2\ – 1,2 = 20,6\) (cm).
Chiều cao của khối bê tông được đúc ra là \(11\ – 1,9 = 9,1\) (cm).
Thể tích của khối bê tông là:
\(10,6\ .\ 20,6\ .\ 9,1 = 218,36\ .\ 9,1 = 1987,076\ (cm^3)\).
Vậy thể tích của khối bê tông là \(1987,076\ cm^3\).
\(\)
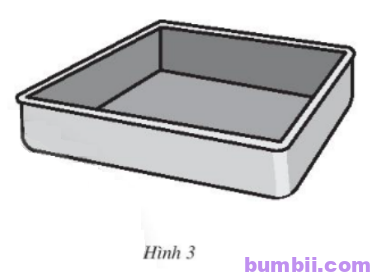
\(4.\) Phần bên trong của một cái khuôn làm bánh có dạng hình hộp chữ nhật với đáy là hình vuông cạnh \(20\) cm, chiều cao \(5\) cm (Hình \(3\)). Người ta dự định sơn phần bên trong bằng loại sơn không dính. Hỏi với một lượng sơn đủ bao phủ được \(100\ m^2\) thì sơn được bao nhiêu cái khuôn làm bánh?
Giải
Diện tích cần sơn của một khuôn làm bánh:
\(S=S_{xq}+S_{đáy}=2.(20+20).5+20^2=800\ (cm^2).\)
Đổi \(800\ cm^2 = 0,08\ m^2\).
Vậy với một lượng sơn đủ bao phủ được \(100\ m^2\) thì sơn được \(100 : 0,08 = 1250\) cái khuôn.
\(\)
\(5.\) Một ngôi nhà có kích thước như Hình \(4\).
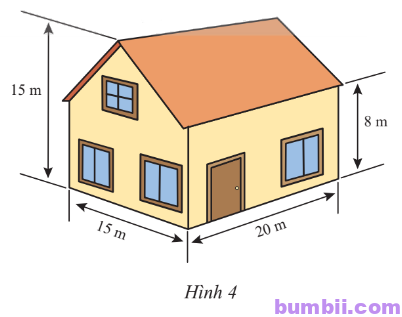
a) Tính thể tích của ngôi nhà.
b) Biết rằng \(1 l\) sơn bao phủ được \(4\ m^2\) tường. Hỏi phải cần ít nhất bao nhiêu lít sơn để sơn phủ được tường mặt ngoài ngôi nhà (không sơn cửa)? Biết tổng diện tích các cửa là \(9\ m^2\).
Giải
a) Diện tích mặt đáy (mặt bên ngôi nhà với 3 cửa sổ nhỏ):
\(15\ .\ 8\ .\ 15\ .\ 7\ :\ 2=172,5\ (m^2).\)
Thể tích của ngôi nhà:
\(172,5.20=3450 (m^2).\)
b) Diện tích cần sơn:
\(2\ .\ 172,5+2\ .\ 20\ .\ 8-9=656\ (m^2)\)
số lít sơn cần có để sơn nhà:
\(656:4=164\) (lít).
Vậy cần \(164\ l\) sơn để phủ được hết mặt ngoài ngôi nhà.
\(\)
\(6.\) Các hình hộp chữ nhật trong Hình \(5\) có cùng số đo thể tích. Em hãy tìm các kích thước còn thiếu.
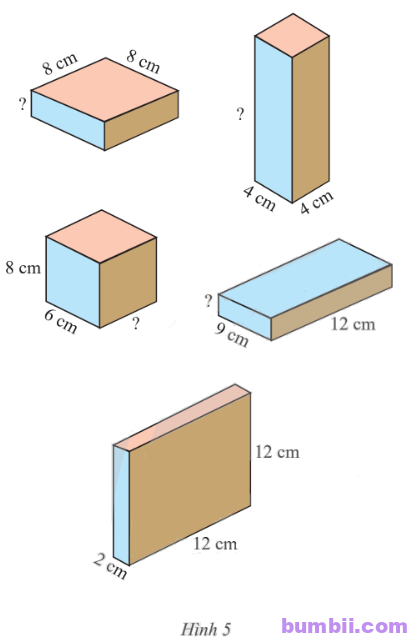
Giải
Thể tích của mỗi hình trong Hình 5 là: \(2 . 12 . 12 = 288\ (cm^3)\).
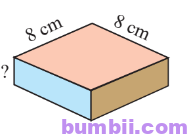
Kích thước còn thiếu trong hình là: \(288 : 8 : 8 = 36 : 8 = 4,5\) (cm).
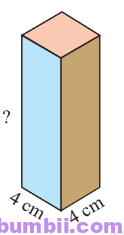
Kích thước còn thiếu trong hình là: \(288 : 4 : 4 = 72 : 4 = 18\) (cm).
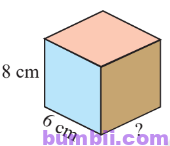
Kích thước còn thiếu trong hình là: \(288 : 8 : 6 = 36 : 6 = 6\) (cm).
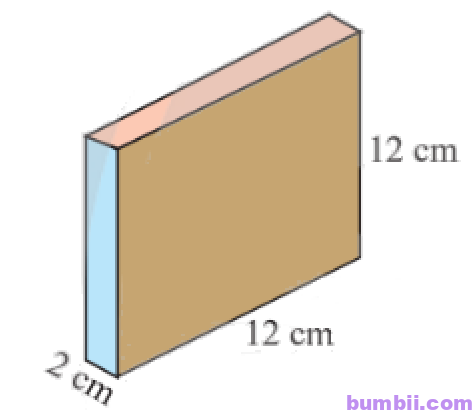
Kích thước còn thiếu trong hình là: \(288 : 12 : 9 = 24 : 9 = \displaystyle\frac{8}{3}\) (cm).
\(\)
\(7.\) Tạo lập hình lăng trụ đứng có chiều cao \(2,5\) cm, đáy là hình thoi có cạnh 3 cm và một góc \(60^o\).
Giải
– Trên một miếng bìa, vẽ bốn hình chữ nhật và hai hình thoi với kích thước như hình dưới.
– Cắt miếng bìa như hình vẽ rồi gấp theo các đường nét đứt, ta được hình lăng trụ đứng hình thoi như hình dưới.
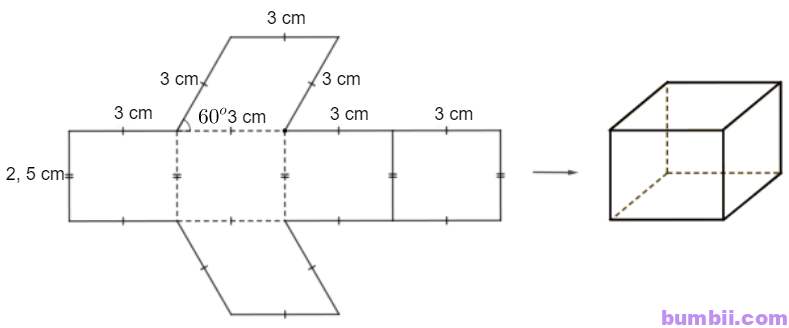
\(\)
\(8.\) Hãy nêu các bước tạo lập hình lăng trụ đứng tam giác trong Hình \(6\).
Giải
Bước 1. Vẽ đoạn thẳng có độ dài \(13\) cm.
Bước 2. Tại \(2\) điểm mút của đoạn thẳng, lần lượt vẽ hai đường tròn có bán kính \(5\) cm và \(12\) cm. Hai đường tròn này cắt nhau tại một điểm.
Nối điểm đó với hai đầu mút của đoạn thẳng, ta được tam giác vuông có độ dài \(3\) cạnh lần lượt là \(5\) cm; \(12\) cm và \(13\) cm.
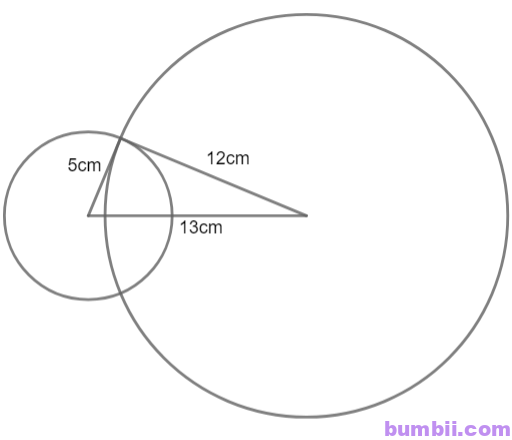
– Trên một miếng bìa, vẽ ba hình chữ nhật và hai tam giác với kích thước như hình dưới.
– Cắt miếng bìa như hình vẽ rồi gấp theo các đường nét đứt, ta được hình lăng trụ đứng tam giác vuông như hình dưới.
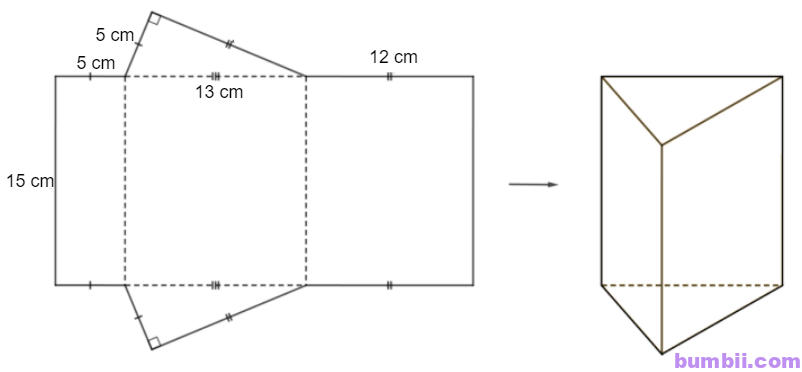
\(\)
\(9.\) Người ta cắt một tấm bìa để tạo lập một lăng trụ đứng có đáy là tam giác đều với kích thước như Hình \(7\). Hãy cho biết độ dài các cạnh đáy và chiều cao của hình lăng trụ đứng đó.
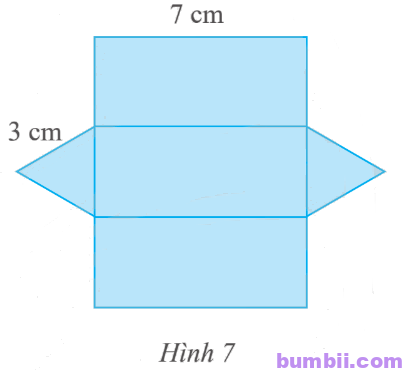
Giải
Độ dài các cạnh đáy của hình lăng trụ là \(3\) cm.
Độ dài chiều cao của hình lăng trụ đứng là \(7\) cm.
Vậy hình lăng trụ đứng có đáy là tam giác đều có độ dài mỗi cạnh đáy đều bằng \(3\) cm và chiều cao là \(7\) cm.
\(\)
Xem thêm các bài giải khác tại: Giải bài tập SGK Toán Lớp 7 – NXB Chân Trời Sáng Tạo.
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech
