Chương 3 – Bài 8: Góc ở vị trí đặc biệt. Tia phân giác của một góc trang 36 sách bài tập toán lớp 7 tập 1 NXB Kết nối tri thức với cuộc sống.
3.1. Cho Hình 3.4, kể tên các cặp góc kề bù.
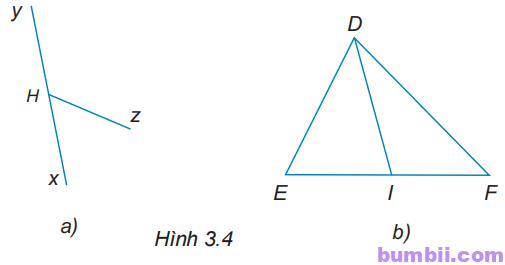
Giải
a) Cặp góc kề bù là \(\widehat{yHz}\) và \(\widehat{zHx}.\)
b) Cặp góc kề bù là \(\widehat{EID}\) và \(\widehat{DIF}.\)
\(\)
3.2. Cho Hình 3.5.
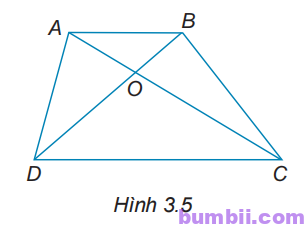
a) Gọi tên các cặp góc đối đỉnh.
b) Gọi tên góc kề bù với \(\widehat{AOD}.\)
Giải
a) Các cặp góc đối đỉnh là \(\widehat{AOB}\) và \(\widehat{DOC};\) \(\widehat{AOD}\) và \(\widehat{BOC}.\)
b) Góc kề bù với \(\widehat{AOD}\) là \(\widehat{AOB}\) và \(\widehat{DOC}.\)
\(\)
3.3. Vẽ hai đường thẳng xy và mn cắt nhau tại điểm O sao cho \(\widehat{xOm}=120^o\). Tính các góc mOy, yOn, xOn.
Giải
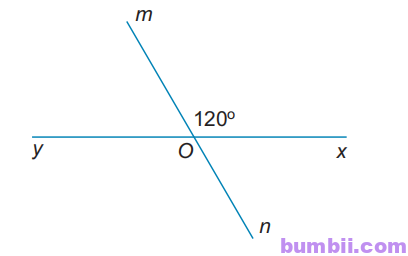
Ta có \(\widehat{yOm} + \widehat{mOx} =180^o\) (hai góc kề bù)
\(\widehat{yOm} +120^o=180^o\)
\(\widehat{yOm} =180^o-120^o=60^o.\)
\(\widehat{yOn}=\widehat{mOx}=120^o\) (hai góc đối đỉnh).
\(\widehat{xOn}=\widehat{mOy}=60^o\) (hai góc đối đỉnh).
\(\)
3.4. Vẽ \(\widehat{xAm}=50^o\). Vẽ tia phân giác An của \(\widehat{xAm}.\)
a) Tính \(\widehat{xAn}.\)
b) Vẽ tia Ay là tia đối của tia An. Tính \(\widehat{mAy}.\)
Giải
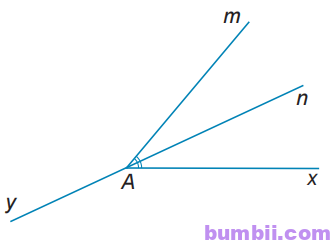
a) Vì An là tia phân giác của \(\widehat{xAm}\) nên:
\(\widehat{xAn}=\widehat{nAm}=\displaystyle\frac{\widehat{xAm}}{2}=\displaystyle\frac{50^o}{2}=25^o.\)
Vậy \(\widehat{xAn}=25^o.\)
b) Ta có \(\widehat{nAm}+\widehat{mAy}=180^o\) (hai góc kề bù)
\(25^o+\widehat{mAy}=180^o\)
\(\widehat{mAy}=180^o-25^o=155^o.\)
Vậy \(\widehat{mAy}=155^o.\)
\(\)
3.5. Cho Hình 3.6. Biết tia Oz là tia phân giác của \(\widehat{xOy}\). Tính \(\widehat{xOy}.\)
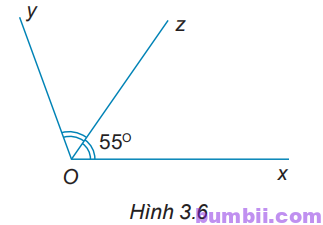
Giải
Vì Oz là tia phân giác của \(\widehat{xOy}\) nên \(\widehat{xOz}=\widehat{zOy}=\displaystyle\frac{\widehat{xOy}}{2}.\)
Do đó \(\widehat{xOy}=2\ .\ \widehat{xOz}=2\ .\ 55^o=110^o.\)
\(\)
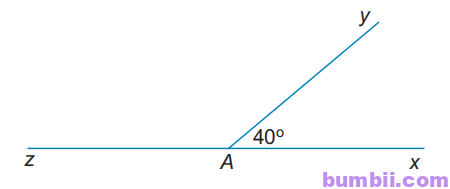
3.6. Vẽ \(\widehat{xAy}=40^o\). Vẽ \(\widehat{yAz}\) là góc kề bù với \(\widehat{xAy}.\)
Giải
\(\)
3.7. Cho góc bẹt xOy. Vẽ tia Oz sao cho \(\widehat{xOz}=60^o\). Vẽ tia Om là tia phân giác của góc xOz. Vẽ tia On là tia phân giác của góc zOy.
a) Tính số đo góc xOm.
b) Tính số đo góc yOn.
c) Tính số đo góc mOn.
Giải
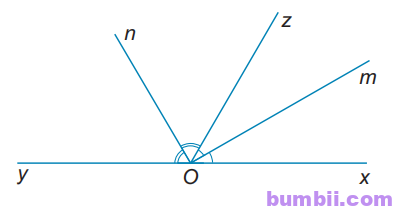
a) Vì Om là tia phân giác của \(\widehat{xOz}\) nên:
\(\widehat{xOm}=\widehat{mOz}=\displaystyle\frac{\widehat{xOz}}{2}=\displaystyle\frac{60^o}{2}=30^o.\)
Vậy \(\widehat{xOm}=30^o.\)
b) Ta có: \(\widehat{yOz}+\widehat{zOx}=180^o\) (hai góc kề bù)
\(\widehat{yOz}+60^o=180^o\)
\(\widehat{yOz}=180^o-60^o=120^o.\)
Tia On là tia phân giác của \(\widehat{yOz}\) nên
\(\widehat{yOn}=\widehat{nOz}=\displaystyle\frac{\widehat{yOz}}{2}=\displaystyle\frac{120^o}{2}=60^o.\)
Vậy \(\widehat{yOn}=60^o.\)
c) Ta có: \(\widehat{mOn}=\widehat{mOz}+\widehat{zOn}\)
\(\widehat{mOn}=30^o+60^o=90^o.\)
Vậy \(\widehat{mOn}=90^o.\)
\(\)
3.8. Vẽ\(\widehat{xOy}=60^o.\) Vẽ tia Oz là tia đối của tia Ox. Vẽ tia Om là tia phân giác của góc zOy.
a) Tính \(\widehat{zOm}.\)
b) Vẽ tia On là tia đối của tia Om. Tia Ox có phải là tia phân giác của góc yOn không? Vì sao?
Giải
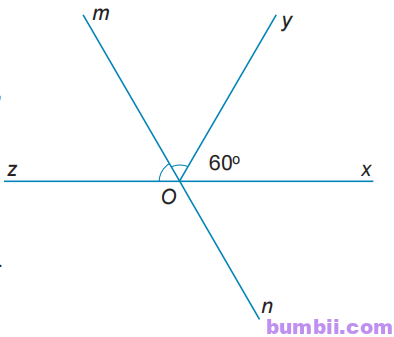
a) Ta có: \(\widehat{xOy}+\widehat{yOz}=180^o\) (hai góc kề bù)
\(60^o+\widehat{yOz}=180^o\)
\(\widehat{yOz}=180^o-60^o=120^o.\)
Tia Om là tia phân giác của \(\widehat{zOy}\) nên
\(\widehat{zOm}=\widehat{mOy}=\displaystyle\frac{\widehat{zOy}}{2}=\displaystyle\frac{120^o}{2}=60^o.\)
Vậy \(\widehat{zOm}=60^o.\)
b) Ta có \(\widehat{xOn}=\widehat{mOz}=60^o\) (hai góc đối đỉnh).
Mặt khác ta có: tia Ox nằm giữa hai tia Oy và On và \(\widehat{xOy}=\widehat{nOx}=60^o\)
Do đó, Ox là tia phân giác của \(\widehat{yOn}.\)
\(\)
Xem bài giải trước: Ôn tập chương II
Xem bài giải tiếp theo: Bài 9: Hai đường thẳng song song và dấu hiệu nhận biết
Xem thêm các bài giải khác tại: Giải Bài tập Toán Lớp 7 – NXB Kết Nối Tri Thức Với Cuộc Sống
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech
