Bài \(7\). Các khái niệm mở đầu trang \(46\) SGK toán lớp \(10\) tập \(1\) Nhà xuất bản Kết nối tri thức với cuộc sống. Các em cùng Bumbii giải các bài tập sau.
Bài \(4.1\). Cho ba vectơ \(\overrightarrow{a}, \overrightarrow{b}, \overrightarrow{c}\) đều khác \(\overrightarrow{0}\). Những khẳng định nào sau đây là đúng?
\(a)\) \(\overrightarrow{a}, \overrightarrow{b}, \overrightarrow{c}\) đều cùng hướng với vectơ \(\overrightarrow{0}\);
\(b)\) Nếu \(\overrightarrow{b}\) không cùng hướng với \(\overrightarrow{a}\) thì \(\overrightarrow{b}\) ngược hướng với \(\overrightarrow{a}\);
\(c)\) Nếu \(\overrightarrow{a}\) và \(\overrightarrow{b}\) đều cùng phương với \(\overrightarrow{c}\) thì \(\overrightarrow{a}\) và \(\overrightarrow{b}\) cùng phương;
\(d)\) Nếu \(\overrightarrow{a}\) và \(\overrightarrow{b}\) đều cùng hướng với \(\overrightarrow{c}\) thì \(\overrightarrow{a}\) và \(\overrightarrow{b}\) cùng hướng.
Trả lời:
Mọi vectơ đều cùng hướng với vectơ \(\overrightarrow{0}\) nên \(a)\) đúng
Nếu vectơ \(\overrightarrow{b}\) không cùng hướng với vectơ \(\overrightarrow{a}\) thì vec tơ \(\overrightarrow{b}\) ngược hướng với vectơ \(\overrightarrow{a}\) hoặc hai vectơ không cùng phương nên \(b)\) sai.
Nếu \(\overrightarrow{a}\) và \(\overrightarrow{b}\) đều cùng phương với \(\overrightarrow{c}\) thì \(\overrightarrow{a}\) và \(\overrightarrow{b}\) có giá song song hoặc trùng với giá của \(\overrightarrow{c}\). Suy ra \(\overrightarrow{a}\) và \(\overrightarrow{b}\) có giá song song hoặc trùng nhau nên \(\overrightarrow{a}\) và \(\overrightarrow{b}\) cùng phương. Vậy \(c)\) đúng
Suy ra \(d)\) đúng (hai vectơ cùng phương và cùng chiều nên cùng hướng)
\(\)
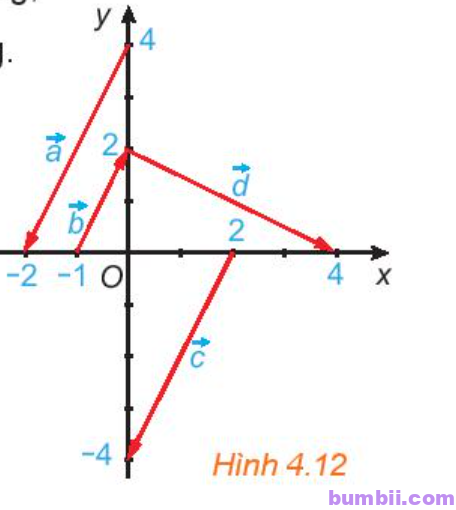
Bài \(4.2\). Trong Hình \(4.12\), hãy chỉ ra các vectơ cùng phương, các cặp vectơ ngược hướng và các cặp vectơ bằng nhau.
Trả lời:
Quan sát hình vẽ ta thấy:
Các vectơ \(\overrightarrow{a}, \overrightarrow{b}, \overrightarrow{c}\) có giá song song với nhau
Các vectơ \(\overrightarrow{a}, \overrightarrow{c}, \overrightarrow{d}\) có độ dài bằng nhau (cạnh huyền trong tam giác vuông có hai cạnh góc vuông với độ lớn là \(2\) và \(4\) đơn vị)
Suy ra:
Các vectơ cùng phương là: \(\overrightarrow{a}, \overrightarrow{b}, \overrightarrow{c}\)
Các cặp vectơ ngược hướng là: \(\overrightarrow{a}\) và \(\overrightarrow{b}\), \(\overrightarrow{b}\) và \(\overrightarrow{c}\)
Các cặp vectơ bằng nhau là: \(\overrightarrow{a}\) và \(\overrightarrow{c}\) cùng hướng và có độ lớn bằng nhau.
\(\)
Bài \(4.3\). Chứng minh rằng tứ giác \(ABCD\) là hình bình hành khi và chỉ khi \(\overrightarrow{BC} = \overrightarrow{AD}\).
Trả lời:
Tứ giác \(ABCD\) là hình bình hành khi và chỉ khi:
\(\left \{\begin{matrix}AD // BC\\AD = BC \end{matrix} \right.\)
\(\Leftrightarrow \left \{\begin{matrix}AD//BC\\|\overrightarrow{AD}| = |\overrightarrow{BC}| \end{matrix} \right.\)
\(\Leftrightarrow \overrightarrow{AD} = \overrightarrow{BC}\) (đpcm)
\(\)
Bài \(4.4\). Cho hình vuông \(ABCD\) có hai đường chéo cắt nhau tại \(O\). Hãy chỉ ra tập hợp \(S\) gồm tất cả các vectơ khác \(\overrightarrow{0}\), có điểm đầu và điểm cuối thuộc tập hợp \(\{A; B; C; D; O\}\). Hãy chia tập \(S\) thành các nhóm sao cho hai vectơ thuộc cùng một nhóm khi và chỉ khi chúng bằng nhau.
Trả lời:
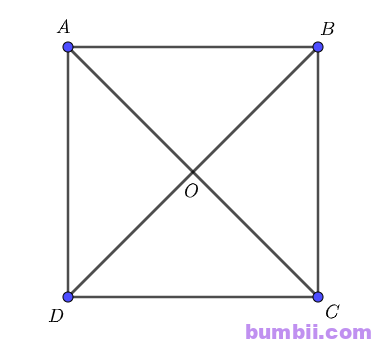
Tập hợp \(S\) bao gồm:
\(S = \{\overrightarrow{AB}, \overrightarrow{AC}, \overrightarrow{AD}, \overrightarrow{AO}, \overrightarrow{BA}, \overrightarrow{BC}, \overrightarrow{BD}, \overrightarrow{BO}, \overrightarrow{CA},\)
\(\overrightarrow{CB}, \overrightarrow{CD}, \overrightarrow{CO}, \overrightarrow{OA}, \overrightarrow{OB}, \overrightarrow{OC}, \overrightarrow{OD}\}\)
Các nhóm trong \(S\) bao gồm:
\(\{\overrightarrow{AB}, \overrightarrow{DC}\}, \{\overrightarrow{BA}, \overrightarrow{CD}\},\{\overrightarrow{AD}, \overrightarrow{BC}\}, \{\overrightarrow{DA}, \overrightarrow{CB}\},\)
\(\{\overrightarrow{OA}, \overrightarrow{CO}\}, \{\overrightarrow{AO}, \overrightarrow{OC}\}, \{\overrightarrow{OB}, \overrightarrow{DO}\}, \{\overrightarrow{BO}, \overrightarrow{OD}\}\)
\(\)
Bài \(4.5\). Trên mặt phẳng toạ độ \(Oxy\), hãy vẽ các vectơ \(\overrightarrow{OA}, \overrightarrow{MN}\) với \(A(1; 2), M(0; \ – \ 1), N(3; 5)\).
\(a)\) Chỉ ra mối quan hệ giữa hai vectơ trên.
\(b)\) Một vật thể khởi hành từ \(M\) và chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu diễn bới vectơ \(\overrightarrow{v} = \overrightarrow{OA}\). Hỏi vật thể đó có đi qua \(N\) hay không? Nếu có thì sau bao lâu vật sẽ tới \(N\)?
Trả lời:
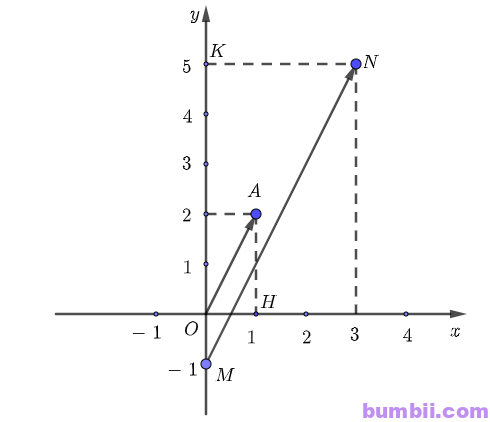
\(a)\) Nhìn vào hình vẽ ta thấy, hai vectơ \(\overrightarrow{OA}\) và \(\overrightarrow{MN}\) là hai vectơ cùng hướng.
\(b)\) Gọi \(H, K\) lần lượt là hình chiếu vuông góc của điểm \(A\) lên trục \(Ox\), điểm \(N\) lên trục \(Oy\).
Xét tam giác \(OAH\) vuông tại \(H\) ta có:
\(OA^2 = OH^2 + AH^2 = 1^2 + 2^2 = 5\)
\(\Rightarrow OA = \sqrt{5}\)
Xét tam giác \(MNK\) vuông tại \(K\), ta có:
\(MN^2 = MK^2 + KN^2 = 6^2 + 3^2 = 45\)
\(\Rightarrow MN = 3\sqrt{5}\)
\(\Rightarrow MN = 3 OA\)
Mà \(\overrightarrow{OA}\) và \(\overrightarrow{MN}\) là hai vectơ cùng hướng
Nên vật thể khởi hành từ \(M\) chuyển động thẳng đều với vận tốc được biểu diễn bởi vectơ \(\overrightarrow{v} = \overrightarrow{OA}\) nên vật thể đó sẽ đi qua điểm \(N\) và sau \(3\) giờ thì vật thể sẽ tới \(N\).
\(\)
Xem bài giải trước: https://bumbii.com/bai-tap-cuoi-chuong-iii-3/
Xem bài giải tiếp theo: https://bumbii.com/bai-8-tong-va-hieu-cua-hai-vecto/
Xem các bài giải khác: https://bumbii.com/giai-bai-tap-sgk-toan-lop-10-nxb-ket-noi-tri-thuc-voi-cuoc-song/
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech

Hạnh phúc đạt được khi bạn ngừng chờ đợi điều đó xảy ra và thực hiện các bước để biến nó thành hiện thực.