Bài \(3\). Hàm số liên tục trang \(73\) SGK Toán lớp \(11\) tập \(1\) Cánh diều. Các em cùng Bumbii giải các bài tập sau:
Bài \(1\). Dùng định nghĩa xét tính liên tục của hàm số \(f(x) = 2x^3 + x + 1\) tại điểm \(x = 2\).
Trả lời:
Hàm số \(f(x) = 2x^3 + x + 1\) xác định trên \(\mathbb{R}\)
Ta có: \(\lim \limits_{x \to 2} f(x) = \lim \limits_{x \to 2} (2x^3 + x + 1)\)
\(= 2. 2^3 + 2 + 1 = 19 = f(2)\)
Do đó hàm số \(f(x)\) liên tục tại \(x = 2\).
\(\)
Bài \(2\). Trong các hàm số có đồ thị ở Hình \(15a, 15b, 15c\), hàm số nào liên tục trên tập xác định của hàm số đó? Giải thích.
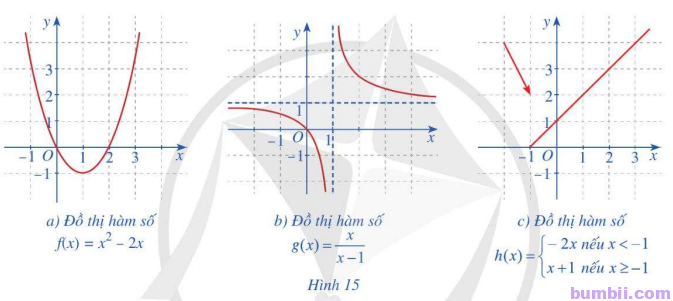
Trả lời:
Xét hình \(15a)\) ta có:
Hàm số \(f(x) = x^2 \ – \ 2x\) có tập xác định \(D = \mathbb{R}\).
Hàm số \(f(x)\) liên tục trên tập xác định \(\mathbb{R}\)
Xét hình \(15b)\) ta có:
Hàm số \(g(x) = \displaystyle \frac{x}{x \ – \ 1}\) có tập xác định \(D = \mathbb{R} \setminus \{1\}\)
Do đó, hàm số \(g(x)\) liên tục trên từng khoảng xác định của hàm số \((\ – \ \infty; 1) \cup (1; +\infty)\)
Xét hình \(15c)\) ta có:
Với \(x \in (\ – \ \infty; \ – \ 1)\) thì \(h(x) = \ – \ 2x\) liên tục trên \((\ – \ \infty; \ – \ 1)\).
Với \(x \in (\ – \ 1; +\infty)\) thì \(h(x) = x + 1\) liên tục trên \((\ – \ 1; +\infty)\)
Tại \(x = \ – \ 1\) có:
\(\lim \limits_{x \to \ – \ 1^-} h(x) = \lim \limits_{x \to \ – \ 1^-} (\ – \ 2x) = \ – \ 2. (\ – \ 1) = 2\)
\(\lim \limits_{x \to 1^+} h(x) = \lim \limits_{x \to 1^+} (x + 1) = \ – \ 1 + 1 = 0\)
\(h(\ – \ 1) = \ – \ 1 + 1 = 0\)
Suy ra \(\lim \limits_{x \to \ – \ 1^-} h(x) \neq \lim \limits_{x \to \ – \ 1^+} = h(\ – \ 1)\)
Do đó hàm số gián đoạn tại \(x = \ – \ 1\)
Vậy hàm số \(h(x)\) liên tục trên các khoảng \((\ – \ \infty; \ – \ 1) \cup (\ – \ 1; +\infty)\)
\(\)
Bài \(3\). Bạn Nam cho rằng: “Nếu hàm số \(y = f(x)\) liên tục tại điểm \(x_0\), còn hàm số \(y = g(x)\) không liên tục tại \(x_0\), thì hàm số \(y = f(x) + g(x)\) không liên tục tại \(x_0\)”. Theo em, ý kiến của bạn Nam đúng hay sai, giải thích.
Trả lời:
Theo em, ý kiến của bạn Nam là đúng.
Giả sử hàm số \(y = f(x) + g(x)\) liên tục tại \(x_0\).
Đặt \(h(x) = f(x) + g(x)\)
\(\Rightarrow g(x) = h(x) \ – \ f(x)\).
Khi đó do \(y = h(x),y = f(x)\) liên tục tại \(x_0\) nên hàm số \(y = g(x)\) phải liên tục tại \(x_0\).
Điều này trái với giả thiết hàm số \(y = g(x)\) không liên tục tại \(x_0\).
Vậy ý kiến của Nam là đúng.
\(\)
Bài \(4\). Xét tính liên tục của mỗi hàm số sau trên tập xác định của hàm số đó:
\(a)\) \(f(x) = x^2 + \sin{x}\);
\(b)\) \(g(x) = x^4 \ – \ x^2 + \displaystyle \frac{6}{x \ – \ 1}\);
\(c)\) \(h)(x) = \displaystyle \frac{2x}{x \ – \ 3} + \displaystyle \frac{x \ – \ 1}{x + 4}\).
Trả lời:
\(a)\) \(f(x) = x^2 + \sin{x}\)
Ta có: \(y = x^2\) là hàm đa thức nên hàm số liên tục trên \(\mathbb{R}\).
\(y = \sin{x}\) là hàm lượng giác nên liên tục trên \(\mathbb{R}\).
Do đó hàm số \(y = x^2 + \sin{x}\) liên tục trên \(\mathbb{R}\).
\(b)\) Hàm số \(g(x)\) có tập xác định là \(D = \mathbb{R} \setminus \{1\}\).
Ta có: Hàm số \(y = x^4 \ – \ x^2\) là hàm đa thức nên liên tục trên \(\mathbb{R}\)
Do đó hàm số \(y = x^4 \ – \ x^2 + \displaystyle \frac{6}{x \ – \ 1}\) liên tục trên các khoảng \((\ – \ \infty; 1)\) và \((1; +\infty)\).
\(c)\) Hàm số có tập xác định \(D = \mathbb{R} \setminus \{3; \ – \ 4\}\).
Hàm số \(h(x) = \displaystyle \frac{2x}{x \ – \ 3} + \displaystyle \frac{x \ – \ 1}{x + 4}\) liên tục trên các khoảng \((\ – \ \infty; \ – \ 4), (\ – \ 4; 3)\) và \((4; +\infty)\).
\(\)
Bài \(5\). Cho hàm số \(f(x) = \begin{equation} \left\{\begin{array}{II} x^2 + x + 1 \text{ nếu } x \neq 4\\2a + 1 \text{ nếu } x = 4. \end{array} \right.\end{equation}\).
\(a)\) Với \(a = 0\), xét tính liên tục của hàm số tại \(x = 4\).
\(b)\) Với giá trị nào của \(a\) thì hàm số liên tục tại \(x = 4\)?
\(c)\) Với giá trị nào của \(a\) thì hàm số liên tục trên tập xác định của nó?
Trả lời:
\(a)\) Tại \(a = 0\) ta có:
\(f(x) = \begin{equation} \left \{\begin{array}{II} x^2 + x + 1 (x \neq 4)\\ 1 \: \: (x = 4)\end{array} \right.\end{equation}\).
Có \(f(4) = 1\)
\(\lim \limits_{x \to 4} f(x) = \lim \limits_{x \to 4} (x^2 + x + 1) = 4^2 + 4 + 1 = 21\)
Ta thấy \(\lim \limits_{x \to 4} f(x) \neq f(4)\)
Suy ra hàm số không liên tục tại \(x = 4\).
\(b)\) Ta có: \(f(4) = 2a + 1\)
\(\lim \limits_{x \to 4} f(x) = 4^2 + 4 + 1 = 21\)
Để hàm số liên tục tại \(x = 1\) thì \(2a + 1 = 21\)
\(\Leftrightarrow a = 10\)
Vậy với \(a = 10\) thì hàm số liên tục tại \(x = 4\).
\(c)\) Hàm số có tập xác định \(\mathbb{R}\).
Do hàm số \(f(x) = x^2 + x + 1\) với mọi \(x \neq 4\) nên hàm số liên tục trên các khoảng \((\ – \ \infty; 4)\) và \((4; +\infty)\)
Với \(a = 10\) thì hàm số liên tục tại \(x = 4\)
Vậy khi \(a = 10\) thì hàm số liên tục trên tập xác định \(\mathbb{R}\).
\(\)
Bài \(6\). Hình \(16\) biểu thị độ cao \(h (m)\) của một quả bóng được đá lên theo thời gian \(t (s)\), trong đó \(h (t) = \ – \ 2t^2 + 8t\).
\(a)\) Chứng tỏ hàm số \(h(t)\) liên tục trên tập xác định.
\(b)\) Dựa vào đồ thị hãy xác định \(\lim \limits_{t \to 2} (\ – \ 2t^2 + 8t)\).
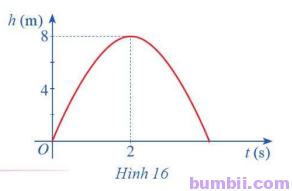
Trả lời:
\(a)\) Ta có \(h(t), t\) lần lượt là độ cao quả bóng và thời gian.
Do đó \(h \geq 0, t \geq 0\)
\(\Rightarrow \ – \ 2t^2 + 8t \geq 0\)
\(\Rightarrow 0 \leq t \leq 4\)
Vậy tập xác định của hàm số là \([0; 4]\).
Trên tập xác định, hàm số là hàm đa thức nên hàm số liên tục trên đoạn \([0; 4]\).
\(b)\) Nhìn vào đồ thị ta thấy:
\(\lim \limits_{x \to 2} (\ – \ 2t^2 + 8t) = 8\)
\(\)
Bài 3. Hàm số liên tục Bài 3. Hàm số liên tục Bài 3. Hàm số liên tục
Xem bài giải trước: Bài 2 – Giới hạn của hàm số
Xem bài giải tiếp theo: Bài tập cuối chương III
Xem các bài giải khác: Giải bài tập SGK Toán Lớp 11 Cánh Diều
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech

Hạnh phúc đạt được khi bạn ngừng chờ đợi điều đó xảy ra và thực hiện các bước để biến nó thành hiện thực.