Bài \(27\). Thực hành tính xác suất theo định nghĩa cổ điển trang \(83\) SGK Toán lớp \(10\) Tập \(2\) Kết nối tri thức với cuộc sống. Các em hãy cùng Bumbii giải các bài tập sau đây nhé.
Bài \(9.6\). Chọn ngẫu nhiên một gia đình có ba con và quan sát giới tính của ba người con này. Tính xác suất của các biến cố sau:
\(a)\) \(A:\) “Con đầu là gái”;
\(b)\) \(B:\) “Có ít nhất một người con trai”.
Trả lời:
Mỗi người con sẽ có hai khả năng xảy ra là trai hoặc gái. Do đó, tổng số khả năng xảy ra khi có \(3\) người con là: \(n(\Omega) = 2. 2. 2 = 8\)
\(a)\) \(A\): Con đầu là con gái (Tức số cách chọn là \(1\))
Hai người con sau, mỗi người có \(2\) cách chọn nên sẽ có tổng \(2. 2 = 4\) (cách chọn)
Do đó, ứng với con đầu là con gái sẽ có số cách chọn hay \(n(A) = 1. 4 = 4\)
Suy ra \(P(A) = \displaystyle \frac{n(A)}{n(\Omega)} = \displaystyle \frac{4}{8} = \displaystyle \frac{1}{2}\)
\(b)\) Biến cố \(B\): “Có ít nhất một người con trai”
\(\Rightarrow\) Biến cố \(\overline{B}\): “Không có người con trai nào”
Ta có: \(\overline{B} = \{G, G, G\}\) nên \(n(\overline{B}) = 1\)
Suy ra \(P(\overline{B}) = \displaystyle \frac{n(\overline{B})}{n(\Omega)} = \displaystyle \frac{1}{8}\)
\(\Rightarrow P(B) = 1 \ – \ P(\overline{B}) = 1 \ – \ \displaystyle \frac{1}{8} = \displaystyle \frac{7}{8}\)
\(\)
Bài \(9.7\). Một hộp đựng các tấm thẻ đánh số \(10; 11; …; 20\). Rút ngẫu nhiên từ hộp hai tấm thẻ. Tính xác suất của các biến cố sau:
\(a)\) \(C:\) “Cả hai thẻ rút được đều mang số lẻ”;
\(b)\) \(D:\) “Cả hai thẻ rút được đều mang số chẵn”.
Trả lời:
Phép thử: Rút ngẫu nhiên \(2\) tấm thẻ từ hộp đựng thẻ
Các tấm thẻ được đánh số từ \(10\) đến \(20\) tức là có tất cả \(11\) tấm thẻ.
Mỗi cách chọn ngẫu nhiên \(2\) tấm thẻ từ \(11\) tấm thẻ là tổ hợp chập \(2\) của \(11\) phần tử.
Khi đó ta có không gian mẫu của phép thử là:
\(n(\Omega) = C_{11}^2 = 55\)
\(a)\) Cả hai thẻ rút ra được đều mang số lẻ tức là hai thẻ đó thuộc tập hợp \(\{11; 13; 15; 17; 19\}\).
\(\Rightarrow n(C) = C_5^2 = 10\)
Suy ra \(P(C) = \displaystyle \frac{n(C)}{n(\Omega)} = \displaystyle \frac{10}{55} = \displaystyle \frac{2}{11}\)
\(b)\) Cả hai thẻ rút ra được đều mang số chẵn tức là hai thẻ đó thuộc tập hợp \(\{10; 12; 14; 16; 18; 20\}\)
\(\Rightarrow n(D) = C_6^2 = 15\)
Suy ra \(P(D) = \displaystyle \frac{n(D)}{n(\Omega)} = \displaystyle \frac{15}{55} = \displaystyle \frac{3}{11}\)
\(\)
Bài \(9.8\). Một chiếc hộp đựng \(6\) viên bi trắng, \(4\) viên bi đỏ và \(2\) viên bi đen. Chọn ngẫu nhiên ra \(6\) viên bi. Tính xác suất để trong \(6\) viên bi đó có \(3\) viên bi trắng, \(2\) viên bi đỏ và \(1\) viên bi đen.
Trả lời:
Tổng số viên bi trong hộp là:
\(6 + 4 + 2 = 12\) (viên bi)
Chọn ngẫu nhiên \(6\) viên bi từ \(12\) viên bi nên ta có số cách chọn là: \(C_{12}^6 = 924\) (cách)
\(\Rightarrow n(\Omega) = 924\)
Biến cố \(A\): Chọn ra \(6\) viên bi gồm \(3\) viên bi trắng, \(2\) viên bi đỏ, \(1\) viên bi đen có \(3\) công đoạn:
Công đoạn \(1\): Chọn \(3\) viên bi trắng trong \(6\) viên bi trắng, ta có số cách chọn là:
\(C_6^3 = 20\) (cách)
Công đoạn \(2\): Chọn \(2\) viên bi đỏ trong \(4\) viên bi đỏ, ta có số cách chọn là:
\(C_4^2 = 6\) (cách)
Công đoạn \(3\): Chọn \(1\) viên bi đen trong \(2\) viên bi đen, ta có số cách chọn là:
\(C_2^1 = 2\) (cách)
Vậy số kết quả thuận lợi cho biến cố \(A\) là:
\(20. 6. 2 = 240\) hay \(n(A) = 240\)
Vậy \(P(A) = \displaystyle \frac{n(A)}{n(\Omega)} = \displaystyle \frac{240}{924} = \displaystyle \frac{20}{77}\)
\(\)
Bài \(9.9\). Gieo liên tiếp một con xúc xắc và một đồng xu.
\(a)\) Vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.
\(b)\) Tính xác suất của các biến cố sau:
\(F\): “Đồng xu xuất hiện mặt ngửa”;
\(G\): “Đồng xu xuất hiện mặt sấp hoặc số chấm xuất hiện trên con xúc xắc là \(5\)”.
Trả lời:
\(a)\) Gieo liên tiếp một con xúc xắc cân đối và một đồng xu nên các kết quả xảy ra đồng khả năng.
Gieo một con xúc xắc, các kết quả có thể xảy ra là \(1\) chấm, \(2\) chấm, \(3\) chấm, \(4\) chấm, \(5\) chấm, \(6\) chấm.
Gieo đồng xu, các kết quả có thể xảy ra là mặt sấp (\(S\)) hoặc mặt ngửa (\(N\)).
Khi đó, ta có sơ đồ hình cây mô tả các phần tử của không gian mẫu là:
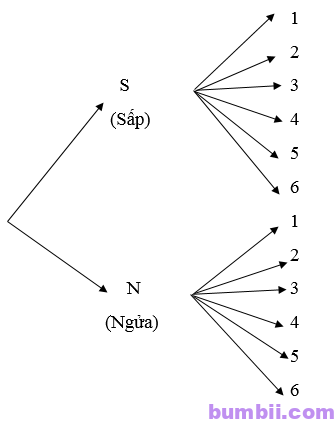
Ta có: \(n(\Omega) = 12\)
\(b)\) Biến cố \(F\): “Đồng xu xuất hiện mặt ngửa”
\(F = \{(N1; N2; N3; N4; N5; N6\}\)
\(\Rightarrow n(F) = 6\)
Vậy \(P(F) = \displaystyle \frac{n(F)}{n(\Omega)} = \displaystyle \frac{6}{12} = \displaystyle \frac{1}{2}\)
Biến cố \(G\): “Đồng xu xuất hiện mặt sấp hoặc số chấm xuất hiện trên con xúc xắc là \(5\)”.
\(G = \{S1; S2; S3; S4; S5; S6; N5\}\)
\(\Rightarrow n(G) = 7\)
Vậy \(P(G) = \displaystyle \frac{n(G)}{n(\Omega)} = \displaystyle \frac{7}{12}\)
\(\)
Bài \(9.10\). Trên một phố có hai quán ăn \(X, Y\). Ba bạn Sơn, Hải, Văn mỗi người chọn ngẫu nhiên một quán ăn.
\(a)\) Vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.
\(b)\) Tính xác suất của biến cố “Hai bạn vào quán \(X\), bạn còn lại vào quán \(Y\)”.
Trả lời:
\(a)\)
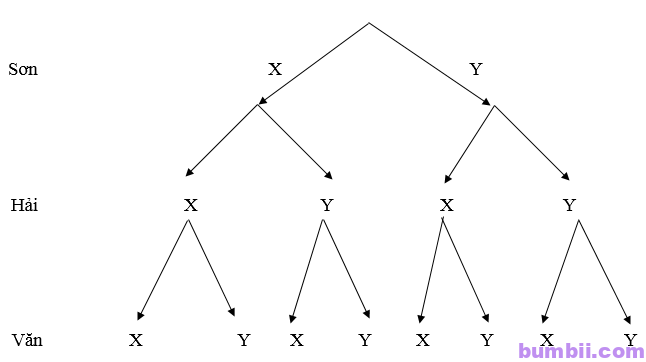
\(b)\) Nhìn vào sơ đồ ta thấy \(n(\Omega) = 8\)
Gọi \(A\) là biến cố: “Hai bạn vào quán \(X\), bạn còn lại vào quán \(Y\)”.
Khi đó ta có \(A = \{XXY, XYX, YXX\}\)
\(\Rightarrow n(A) = 3\)
Vậy \(P(A) = \displaystyle \frac{n(A)}{n(\Omega)} = \displaystyle \frac{3}{8}\)
\(\)
Bài \(9.11\). Gieo lần lượt hai con xúc xắc cân đối. Tính xác suất để ít nhất một con xúc xắc xuất hiện mặt \(6\) chấm.
Trả lời:
Gieo lần lượt hai con xúc xắc cân đối nên các kết quả xảy ra là đồng khả năng. Mỗi con xúc xắc có \(6\) kết quả xảy ra (\(1; 2; 3; 4; 5; 6\) chấm). Khi đó tổng số kết quả có thể xảy ra khi gieo hai con xúc xắc là:
\(6. 6 = 36\)
Suy ra \(n(\Omega) = 36\)
Gọi \(M\) là biến cố: “Ít nhất một con xúc xắc xuất hiện mặt \(6\) chấm”
Để ít nhất một con xúc xắc xuất hiện mặt \(6\) chấm thì có các trường hợp sau:
Trường hợp \(1\): Một con xuất hiện \(6\) chấm, con còn lại không xuất hiện \(6\) chấm.
Khi đó, số kết quả có thể xảy ra là:
\(1. 5. 2 = 10\)
Trường hợp \(2\): cả hai con xuất hiện \(6\) chấm tức là số kết quả xảy ra là \(1\)
Theo quy tắc cộng, ta có số kết quả thuận lợi cho biến cố \(M\) là: \(10 + 1 = 11\) hay \(n(M) = 11\)
Vậy \(P(M) = \displaystyle \frac{n(M)}{n(\Omega)} = \displaystyle \frac{11}{36}\)
\(\)
Bài \(9.12\). Màu hạt của đậu Hà Lan có hai kiểu hình là màu vàng và màu xanh tương ứng với hai loại gen là gen trội \(A\) và gen lặn \(a\). Hình dạng hạt của đậu Hà Lan có hai kiểu hình là hạt trơn và hạt nhăn tương ứng với hai loại gen là gen trội \(B\) và gen lặn \(b\). Biết rằng, cây con lấy ngẫu nhiên một gen từ cây bố và một gen từ cây mẹ.
Phép thử cho lai hai loại đậu Hà Lan, trong đó cả cây bố và cây mẹ đều có kiểu gen là (\(Aa, Bb\)) và kiểu hình là hạt màu vàng và trơn. Giả sử các kết quả có thể là đồng khả năng. Tính xác suất để cây con cũng có kiểu hình là hạt màu vàng và trơn.
Trả lời:
Các kết quả có thể của kiểu gen ứng với màu hạt của cây con là \(AA, Aa, aA, aa\).
Các kết quả có thể của kiểu gen ứng với dạng hạt của cây con là \(BB, Bb, bB, bb\).
Khi đó, theo quy tắc nhân, ta có số kết quả có thể của cây con (bao gồm màu hạt và dạng hạt) hay số phần tử của không gian mẫu là:
\(n(\Omega) = 4. 4 = 16\)
Gọi \(M\) là biến cố: “Cây con có hạt màu vàng và trơn”.
Cây con có hạt màu vàng và trơn khi và chỉ khi trong kiểu gen màu hạt có ít nhất một gen trội \(A\) và trong kiểu gen dạng hạt có ít nhất một gen trội \(B\).
Do đó, \(M = \{(AA, BB), (Aa, BB), (aA, BB), (AA, Bb),\)
\( (AA, bB), (Aa, Bb), (Aa, bB), (aA, Bb), (aA, bB)\}\)
\(\Rightarrow n(M) = 9\)
Vậy \(P(M) = \displaystyle \frac{n(M)}{n(\Omega)} = \displaystyle \frac{9}{16}\)
\(\)
Xem bài giải trước: Bài 26 – Biến cố và định nghĩa cổ điển của xác suất
Xem bài giải tiếp theo: Bài tập cuối chương IX
Xem các bài giải khác: Giải bài tập SGK Toán Lớp 10 – Kết nối tri thức với cuộc sống
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech

Hạnh phúc đạt được khi bạn ngừng chờ đợi điều đó xảy ra và thực hiện các bước để biến nó thành hiện thực.