Bài \(19\). Phương trình đường thẳng trang \(30\) SGK toán lớp \(10\) tập \(2\) Nhà xuất bản Kết nối tri thức với cuộc sống. Các em cùng Bumbii giải các bài tập sau.
Bài \(7.1\). Trong mặt phẳng toạ độ, cho \(\overrightarrow{n} = (2; 1), \overrightarrow{v} = (3; 2); A(1; 3); B(\ – \ 2; 1)\).
\(a)\) Lập phương trình tổng quát của đường thẳng \(\Delta_1\) đi qua \(A\) và có vectơ pháp tuyến \(\overrightarrow{n}\).
\(b)\) Lập phương trình tham số của đường thẳng \(\Delta_2\) đi qua \(B\) và có vectơ chỉ phương \(\overrightarrow{v}\).
\(c)\) Lập phương trình tham số của đường thẳng \(AB\).
Trả lời:
\(a)\) Đường thẳng \(\Delta_1\) đi qua \(A\) và có vectơ pháp tuyến \(\overrightarrow{n}\) nên có phương trình tổng quát là:
\(2. (x \ – \ 1) + 1. (y \ – \ 3) = 0\)
\(\Leftrightarrow 2x + y \ – \ 5 = 0\)
\(b)\) Đường thẳng \(\Delta_2\) đi qua \(B\) và có vectơ chỉ phương \(\overrightarrow{v}\) nên có phương trình tham số là:
\(\left \{\begin{matrix}x = \ – \ 2 + 3t\\y = 1 + 2t \end{matrix} \right.\)
\(c)\) Ta có: \(\overrightarrow{AB} = (\ – \ 2 \ – \ 1; 1 \ – \ 3) = (\ – \ 3; \ – \ 2)\)
Đường thẳng \(AB\) đi qua điểm \(A(1; 3)\) và nhận vectơ \(\overrightarrow{AB}\) làm vectơ chỉ phương nên phương trình tham số của đường thẳng \(AB\) là:
\(\left \{\begin{matrix}x = 1 \ – \ 3t\\y = 3 \ – \ 2t \end{matrix} \right.\)
\(\)
Bài \(7.2\). Lập phương trình tổng quát của các trục toạ độ.
Trả lời:
Vectơ đơn vị của trục \(Ox, Oy\) lần lượt là \(\overrightarrow{i} (1; 0), \overrightarrow{j} (0; 1)\).
Các vectơ đơn vị đồng thời cũng là vectơ chỉ phương tương ứng của các trục.
Mà hai trục vuông góc với nhau nên vectơ chỉ phương của trục này sẽ là vectơ pháp tuyến của trục kia.
Trục \(Ox\) đi qua điểm \(O(0; 0)\) và nhận vectơ \(\overrightarrow{j} (0; 1)\) làm vectơ pháp tuyến nên có phương trình tổng quát là:
\(0. (x \ – \ 0) + 1. (y \ – \ 0) = 0\)
\(\Leftrightarrow y = 0\)
Trục \(Oy\) đi qua điểm \(O(0; 0)\) và nhận vectơ \(\overrightarrow{i} (1; 0)\) làm vectơ pháp tuyến nên có phương trình tổng quát là:
\(1. (x \ – \ 0) + 0. (y \ – \ 0) = 0\)
\(\Leftrightarrow x = 0\)
\(\)
Bài \(7.3\). Cho hai đường thẳng \(\Delta_1: \left \{\begin{matrix}x = 1 + 2t\\y = 3 + 5t \end{matrix} \right.\) và \(\Delta_2: 2x + 3y \ – \ 5 = 0\).
\(a)\) Lập phương trình tổng quát của \(\Delta_1\).
\(b)\) Lập phương trình tham số của \(\Delta_2\).
Trả lời:
\(a)\) \(\Delta_1\) đi qua điểm \(A(1; 3)\) và có vectơ chỉ phương \(\overrightarrow{u_1} = (2; 5)\).
Suy ra \(\Delta_1\) có vectơ pháp tuyến là \(\overrightarrow{n_1} = (5; \ – \ 2)\)
Vậy phương trình tổng quát của đường thẳng \(\Delta_1\) là: \(5.( x \ – \ 1) \ – \ 2.(y \ – \ 3) = 0\)
\(\Leftrightarrow 5x \ – \ 2y + 1 = 0\)
\(b)\) Đường thẳng \(\Delta_2\) có phương trình tổng quát: \(2x + 3y \ – \ 5 = 0\) nên \(\Delta_2\) có vectơ pháp tuyến là \(\overrightarrow{n_2} = (2; 3)\).
Suy ra \(\Delta_2\) có vectơ chỉ phương \(\overrightarrow{u_2} = (3; \ – \ 2)\)
Lấy điểm \(B(1; 1) \in \Delta_2\) (Vì \(2. 1 + 3. 1 \ – \ 5 = 0\))
Khi đó đường thẳng \(\Delta_2\) đi qua điểm \(B(1; 1)\) và có vectơ chỉ phương \(\overrightarrow{u_2} = (3; \ – \ 2)\) nên có phương trình tham số là:
\(\left \{\begin{matrix}x = 1 + 3t\\y = 1 \ – \ 2t \end{matrix} \right.\)
\(\)
Bài \(7.4\). Trong mặt phẳng toạ độ, cho tam giác \(ABC\) có \(A(1; 2), B(3; 0), C(\ – \ 2; \ – \ 1)\).
\(a)\) Lập phương trình đường cao kẻ từ \(A\).
\(b)\) Lập phương trình đường trung tuyến kẻ từ \(B\).
Trả lời:
\(a)\) Ta có: \(\overrightarrow{BC} = (\ – \ 2 \ – \ 3; \ – \ 1 \ – \ 0) = (\ – \ 5; \ – \ 1)\)
Đường cao kẻ từ \(A\) tức là đường thẳng đi qua điểm \(A(1; 2)\) và nhận vectơ \(\overrightarrow{BC} = (\ – \ 5; \ – \ 1)\) làm vectơ pháp tuyến.
Vậy phương trình đường cao kẻ từ \(A\) là:
\(\ – \ 5. (x \ – \ 1) \ – \ 1. (y \ – \ 2) = 0\)
\(\Leftrightarrow 5x + y \ – \ 7 = 0\)
\(b)\) Gọi \(M(x_M; y_M)\) là trung điểm của \(AC\).
Khi đó ta có:
\(\left \{\begin{matrix}x_M = \displaystyle \frac{x_A + x_C}{2} = \displaystyle \frac{1 + (\ – \ 2)}{2} = \displaystyle \frac{\ – \ 1}{2}\\y_M = \displaystyle \frac{y_A + y_C}{2} = \displaystyle \frac{2 + (\ – \ 1)}{2} = \displaystyle \frac{1}{2} \end{matrix} \right.\).
Suy ra \(M\left(\displaystyle \frac{\ – \ 1}{2}; \displaystyle \frac{1}{2}\right)\).
Đường trung tuyến kẻ từ \(B\) chính là đường thẳng đi qua \(B\) và nhận vectơ \(\overrightarrow{BM} = \left(\displaystyle \frac{\ – \ 7}{2}; \displaystyle \frac{1}{2}\right)\) làm vectơ chỉ phương.
Vậy phương trình tham số của đường thẳng \(BM\) là:
\(\left \{\begin{matrix}x = 3 \ – \ \displaystyle \frac{7}{2}t\\y = \displaystyle \frac{1}{2}t \end{matrix} \right.\)
\(\)
Bài \(7.5\). (Phương trình đoạn chắn của đường thẳng)
Chứng minh rằng, đường thẳng đi qua hai điểm \(A(a; 0), B(0; b)\) với \(ab \neq 0 (H.7.3)\) có phương trình là: \(\displaystyle \frac{x}{a} + \displaystyle \frac{y}{b} = 1\).
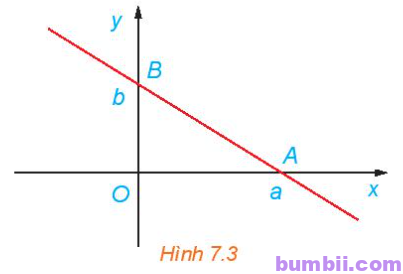
Trả lời:
Ta có: \(\overrightarrow{AB} = (0 \ – \ a; b \ – \ 0) = (\ – \ a; b)\)
Suy ra đường thẳng \(AB\) có vectơ chỉ phương \(\overrightarrow{AB} = (\ – \ a; b)\) nên có vectơ pháp tuyến là \(\overrightarrow{n} = (b; a)\)
Do đó, đường thẳng \(AB\) đi qua điểm \(A\) và có vectơ pháp tuyến \(\overrightarrow{n} = (b; a)\) nên có phương trình tổng quát là:
\(b( x \ – \ a) + a( y \ – \ 0) = 0\)
\(\Leftrightarrow bx + ay \ – \ ab = 0\)
Do \(ab \neq 0\) nên ta chia cả hai vế của phương trình trên cho \(ab\), ta được:
\(\displaystyle \frac{bx}{ab} + \displaystyle \frac{ay}{ab} \ – \ \displaystyle \frac{ab}{ab} = 0\)
\(\Leftrightarrow \displaystyle \frac{x}{a} + \displaystyle \frac{y}{b} \ – \ 1 = 0\)
\(\Leftrightarrow \displaystyle \frac{x}{a} + \displaystyle \frac{y}{b} = 1\)
Vậy phương trình đường thẳng đi qua hai điểm \(A(a; 0), B(0; b)\) với \(ab \neq 0 \) có phương trình là: \(\displaystyle \frac{x}{a} + \displaystyle \frac{y}{b} = 1\). (đpcm)
\(\)
Bài \(7.6\). Theo Google Maps, sân bay Nội Bài có vĩ độ \(21,2^o\) Bắc, kinh độ \(105,8^o\) Đông, sân bay Đà Nẵng có vĩ độ \(16,1^o\) Bắc, kinh độ \(108,2^o\) Đông. Một máy bay bay từ Nội Bài đến sân bay Đà Nẵng. Tại thời điểm \(t\) giờ, tính từ lúc xuất phát, máy bay ở vị trí có vĩ độ \(x^o\) Bắc, kinh độ \(y^o\) Đông được tính theo công thức:
\(\left \{\begin{matrix}x = 21,2 \ – \ \displaystyle \frac{153}{40}t\\y = 105,8 + \displaystyle \frac{9}{5}t \end{matrix} \right.\)
\(a)\) Hỏi chuyến bay từ Hà Nội đến Đà Nẵng mất mấy giờ?
\(b)\) Tại thời điểm \(1\) giờ kể từ lúc cất cánh, máy bay đã bay qua vĩ tuyến \(17 (17^o \text{ Bắc })\) chưa?
Trả lời:
\(a)\) Tại Nội Bài, máy bay bắt đầu xuất phát ứng với \(t = 0\).
Tại thời điểm \(t\), tọa độ của vị trí máy bay thỏa mãn:
\(\left \{\begin{matrix}x = 21,2 \ – \ \displaystyle \frac{153}{40}t\\y = 105,8 + \displaystyle \frac{9}{5}t \end{matrix} \right.\)
Khi máy bay bay tới Đà Nẵng, thì tọa độ sân bay Đà Nẵng thỏa mãn hệ, ta có:
\(\left \{\begin{matrix}16,1 = 21,2 \ – \ \displaystyle \frac{153}{40}t\\108,2 = 105,8 + \displaystyle \frac{9}{5}t \end{matrix} \right.\)
\(\Leftrightarrow \left \{\begin{matrix}t = \displaystyle \frac{4}{3}\\t = \displaystyle \frac{4}{3} \end{matrix} \right.\)
Suy ra \(t = \displaystyle \frac{4}{3}\) là nghiệm của hệ.
Vậy chuyến bay từ Hà Nội đến Đà Nẵng mất \(\displaystyle \frac{4}{3}\) giờ.
\(b)\) Tại thời điểm \(1\) giờ kể từ lúc cất cánh, tức là \(t = 1\), thay vào hệ ta được:
\(\left \{\begin{matrix}x = 21,2 \ – \ \displaystyle \frac{153}{40}. 1\\y = 105,8 + \displaystyle \frac{9}{5}. 1\end{matrix} \right.\)
\(\Leftrightarrow \left \{\begin{matrix}x = 17,375\\y = 107,6 \end{matrix} \right.\)
Do đó, tại thời điểm \(1\) giờ kể từ khi cất cánh, máy bay đang ở vị trí \(17,375^o\) Bắc, \(107,6^o\) Đông.
Vậy tại thời điểm \(1\) giờ kể từ lúc cất cánh, máy bay đã bay qua vĩ tuyến \(17 (17^o \text{ Bắc })\).
\(\)
Xem bài giải trước: Bài tập cuối chương VI
Xem bài giải tiếp theo: Bài 20. Vị trí tương đối của hai đường thẳng. Góc và khoảng cách
Xem các bài giải khác: Giải bài tập SGK Toán Lớp 10 – NXB Kết nối tri thức với cuộc sống
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech

Hạnh phúc đạt được khi bạn ngừng chờ đợi điều đó xảy ra và thực hiện các bước để biến nó thành hiện thực.