Chương 4 – Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác trang 60 sách bài tập toán lớp 7 tập 1 NXB Kết nối tri thức với cuộc sống.
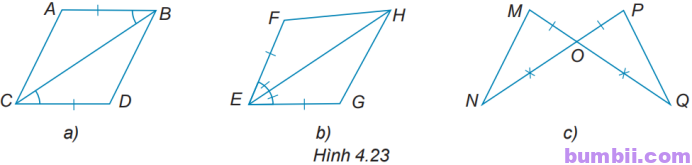
4.21. Trong mỗi hình dưới đây, hãy chỉ ra một cặp tam giác bằng nhau và giải thích vì sao chúng bằng nhau.
Giải
a) Hai tam giác ABC và DCB ta có:
AB = DC (theo giả thiết);
\(\widehat{ABC} = \widehat{DCB}\) (theo giả thiết);
BD là cạnh chung.
Vậy \(\Delta ABC = \Delta DCB\) (c.g.c).
b) Hai tam giác HEF và HEG ta có:
EF = EG (theo giả thiết);
\(\widehat{FEH} = \widehat{GEH}\) (theo giả thiết);
EH là cạnh chung.
Vậy \(\Delta HEF = \Delta HEG\) (c.g.c).
c) Hai tam giác MON và POQ ta có:
OM = OP (theo giả thiết);
\(\widehat{MON} = \widehat{POQ}\) (hai góc đối đỉnh);
ON = OQ (theo giả thiết).
Vậy \(\Delta HEF = \Delta HEG\) (c.g.c).
\(\)
4.22. Cho hai tam giác ABC và DEF bất kỳ, thỏa mãn \(AB = FE,\ BC = DF,\) \(\widehat{ABC} =\widehat{DFE}\). Những câu nào dưới đây đúng?
a) \(∆ABC = ∆DFE.\)
b) \(∆BAC = ∆EFD.\)
c) \(∆CAB = ∆EFD.\)
d) \(∆ABC = ∆EFD.\)
Giải
Vì \(\widehat{ABC} =\widehat{DFE}\) nên đỉnh B tương ứng với đỉnh F;
Vì AB = FE mà đỉnh B ứng với đỉnh F thì đỉnh A ứng với đỉnh E.
Suy ra đỉnh C ứng với đỉnh D.
Vậy chỉ có đáp án d) đúng.
\(\)
4.23. Cho hai tam giác ABC và MNP bất kì, thỏa mãn \(\widehat{ABC} =\widehat{PNM},\) \(\widehat{ACB} =\widehat{NPM}\) và \(BC = PN.\) Những câu nào dưới đây đúng?
a) \(∆ABC = ∆PNM.\)
b) \(∆ABC = ∆NPM.\)
c) \(∆ABC = ∆MPN.\)
d) \(∆ABC = ∆MNP.\)
Giải
Vì \(\widehat{ABC} =\widehat{PNM}\) nên đỉnh B tương ứng với đỉnh N.
Vì \(\widehat{ACB} =\widehat{NPM}\) nên đỉnh C tương ứng với đỉnh P.
Suy ra đỉnh A tương ứng với đỉnh M.
Vậy chỉ có đáp án d) đúng.
\(\)
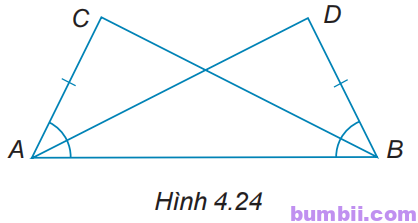
4.24. Cho các điểm A, B, C, D như Hình 4.24, biết rằng \(AC = BD\) và \(\widehat{DBA} =\widehat{CAB}.\)
Chứng minh rằng \(AD = BC.\)
Giải
Hai tam giác ABC và BAD ta có:
AC = BD (theo giả thiết);
\(\widehat{DBA} =\widehat{CAB}\) (theo giả thiết);
AB là cạnh chung.
Vậy \(∆ABC = ∆BAD\) (c.g.c).
Do đó AD = BC.
\(\)
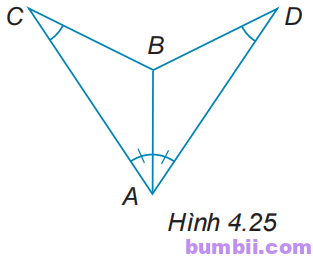
4.25. Cho các điểm A, B, C, D như Hình 4.25, biết rằng \(\widehat{BAC} =\widehat{BAD}\) và \(\widehat{BCA} =\widehat{BDA}.\)
Chứng minh rằng \(∆ABC = ∆ABD.\)
Giải
Xét tam giác ABC có:
\(\widehat{ABC}+\widehat{BAC}+\widehat{BCA}=180^o\)
\(\Rightarrow \widehat{ABC}=180^o-\widehat{BAC}-\widehat{BCA}.\)
Xét tam giác ABD có:
\(\widehat{ABD}+\widehat{BAD}+\widehat{BDA}=180^o\)
\(\Rightarrow \widehat{ABD}=180^o-\widehat{BAD}-\widehat{BDA}.\)
Mà \(\widehat{BAC}=\widehat{BAD};\ \widehat{BCA}=\widehat{BDA}.\)
Suy ra \(\widehat{ABC}=\widehat{ABD}.\)
Hai tam giác ABC và ABD ta có:
\(\widehat{BAC} =\widehat{BAD}\) (theo giả thiết);
AB là cạnh chung;
\(\widehat{ABC} =\widehat{ABD}\) (chứng minh trên).
Vậy \(∆ABC = ∆ABD\) (g.c.g).
\(\)
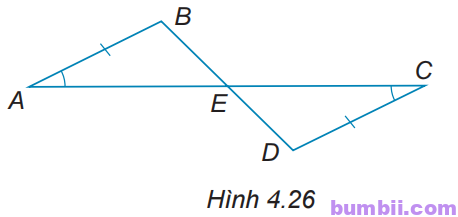
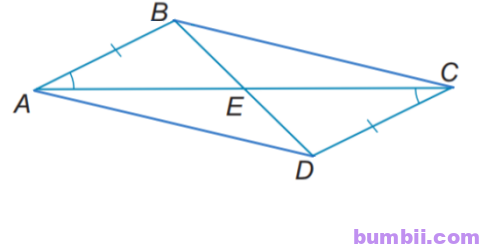
4.26. Cho các điểm A, B, C, D, E như Hình 4.26, biết rằng \(AB = CD,\) \(\widehat{BAE} =\widehat{DCE}.\) Chứng minh rằng:
a) E là trung điểm của các đoạn thẳng AC và BD.
b) \(∆ACD = ∆CAB.\)
c) AD song song với BC.
Giải
a) Xét tam giác ABE có:
\(\widehat{BAE}+\widehat{ABE}+\widehat{AEB}=180^o\)
\(\Rightarrow \widehat{ABE}=180^o-\widehat{BAE}-\widehat{AEB}.\)
Xét tam giác CDE có:
\(\widehat{DCE}+\widehat{DEC}+\widehat{EDC}=180^o\)
\(\Rightarrow \widehat{EDC}=180^o-\widehat{DCE}-\widehat{DEC}.\)
Mà \(\widehat{BAE}=\widehat{DCE}\) (theo giả thiết); \(\widehat{AEB}=\widehat{DEC}\) (hai góc đối đỉnh).
Suy ra \(\widehat{ABE}=\widehat{EDC}.\)
Hai tam giác ABE và CDE ta có:
\(\widehat{ABE}=\widehat{EDC}\) (chứng minh trên);
AB = CD (theo giả thiết);
\(\widehat{BAE} =\widehat{DCE}\) (theo giả thiết).
Vậy \(∆ABE = ∆CDE\) (g.c.g).
Suy ra AE = CE; BE = DE (các cặp cạnh tương ứng)
Vì AE = CE và E nằm giữa A và C nên E là trung điểm của AC;
Vì BE = DE và B nằm giữa D và B nên E là trung điểm của BD.
b) Hai tam giác ACD và CAB có:
CD = AB (theo giả thiết);
AC là cạnh chung;
\(\widehat{ACD}=\widehat{CAB}\) (theo giả thiết).
Vậy \(∆ACD = ∆CAB\) (c.g.c).
c) Vì \(∆ACD = ∆CAB\) nên \(\widehat{CAD} =\widehat{ACB}\) (hai góc tương ứng)
Mà hai góc này ở vị trí so le trong nên AD // BC (dấu hiệu nhận biết hai đường thẳng song song).
Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác
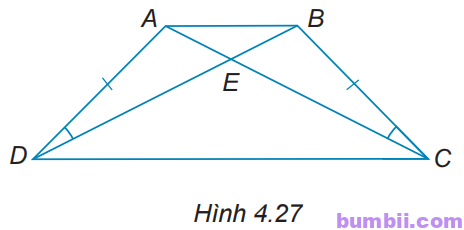
4.27. Cho các điểm A, B, C, D, E như Hình 4.27, biết rằng \(AD = BC,\) \(\widehat{ADE} =\widehat{BCE}.\) Chứng minh rằng:
a) \(\widehat{DAC} =\widehat{CBD}.\)
b) \(∆AED = ∆BEC.\)
c) AB song song với DC.
Giải
a) Xét tam giác AED có:
\(\widehat{DAE}+\widehat{ADE}+\widehat{AEB}=180^o\)
Xét tam giác BEC có:
\(\widehat{EBC}+\widehat{BEC}+\widehat{BCE}=180^o\)
Mà \(\widehat{ADE}=\widehat{BCE}\) (theo giả thiết); \(\widehat{AED}=\widehat{BEC}\) (hai góc đối đỉnh).
Suy ra \(\widehat{DAE}=\widehat{EBC}\) hay \(\widehat{DAC}=\widehat{CBD}.\)
b) Hai tam giác AED và BEC ta có:
\(\widehat{DAE}=\widehat{EBC}\) (chứng minh trên);
AD = BC (theo giả thiết);
\(\widehat{ADE} =\widehat{BCE}\) (theo giả thiết).
Vậy \(∆ABE = ∆CDE\) (g.c.g).
c) Vì \(∆AED = ∆BEC\) nên AE = BE; ED = EC (cặp cạnh tương ứng)
Ta có: AC = AE + EC; BD = BE + ED.
Do đó AC = BD.
Hai tam giác ADB và BCA ta có:
AC = BD (chứng minh trên);
AB là cạnh chung;
AD = BC (theo giả thiết).
Vậy \(∆ADB = ∆BCA\) (c.c.c)
Suy ra \(\widehat{ABD}=\widehat{BAC}\) (hai góc tương ứng).
Hai tam giác ACD và BDC ta có:
AC = BD (chứng minh trên);
CD là cạnh chung;
AD = CB (theo giả thiết).
Vậy \(∆ACD = ∆BDC\) (c.c.c).
Suy ra \(\widehat{ACD}=\widehat{BDC}\) (hai góc tương ứng).
Như vậy \(2\widehat{ABD}=\widehat{ABE}+\widehat{BAE}=180^o-\widehat{AEB}\) \(=180^o-\widehat{DEC}\) \(=\widehat{ECD}+\widehat{EDC}=2\widehat{BDC}.\)
Do đó \(\widehat{ABD}=\widehat{BDC},\) suy ra AB // DC (vì hai góc so le trong bằng nhau).
\(\)
4.28. Cho tam giác ABC bằng tam giác DEF (H.4.28).
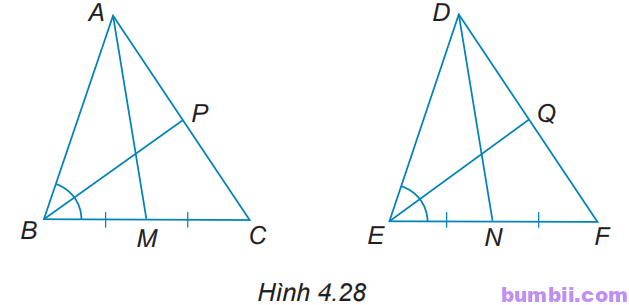
a) Gọi M và N lần lượt là trung điểm các đoạn thẳng BC và EF. Chứng minh rằng AM = DN.
b) Trên hai cạnh AC và DF lấy hai điểm P và Q sao cho BP, EQ lần lượt là phân giác của các góc \(\widehat{ABC}\) và \(\widehat{DEF}\). Chứng minh rằng: BP = EQ.
Giải
a) Vì \(∆ABC = ∆DEF\) nên:
AB = DE (hai cạnh tương ứng);
\(\widehat{ABC}=\widehat{DEF}\) (hai góc tương ứng).
Hai tam giác ABM và DEN ta có:
BM = EN (theo giả thiết);
\(\widehat{ABC}=\widehat{DEF}\);
AB = DE.
Vậy \(∆ABM = ∆DEN\) (c.g.c).
Suy ra AM = DN (hai cạnh tương ứng).
b) Hai tam giác ABP và DEQ ta có:
\(\widehat{ABP}=\widehat{DEQ}\) \(\left(=\displaystyle\frac{1}{2}\widehat{ABC}=\displaystyle\frac{1}{2}\widehat{DEF}\right).\)
AB = DE;
\(\widehat{BAP}=\widehat{EDQ}\) (do \(\widehat{ABC}=\widehat{DEF}\)).
Vậy \(∆ABP = ∆DEQ\) (g.c.g).
Suy ra BP = EQ (hai cạnh tương ứng).
\(\)
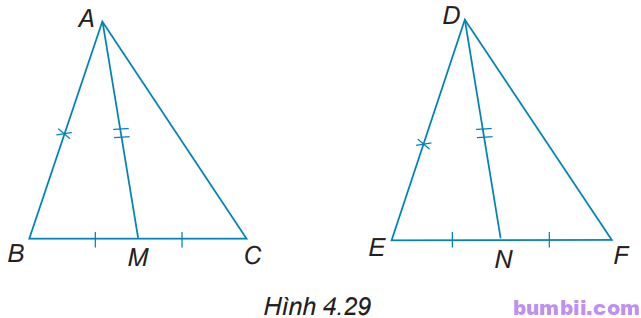
4.29. Gọi M và N lần lượt là trung điểm các đoạn thẳng cạnh BC và EF của hai tam giác ABC và DEF. Giả sử rằng AB = DE, BC = EF, AM = DN (H.4.29). Chứng minh rằng \(∆ABC = ∆DEF.\)
Giải
Vì M là trung điểm của BC nên BM = MC = \(\displaystyle\frac{BC}{2}.\)
Vì N là trung điểm của EF nên EN = NF = \(\displaystyle\frac{EF}{2}.\)
Mà BC = EF (theo giả thiết) nên BM = EN.
Hai tam giác ABM và DEN ta có:
AB = DE (theo giả thiết);
BM = EN (chứng minh trên);
AM = DN (theo giả thiết).
Vậy \(∆ABM = ∆DEN\) (c.c.c).
Suy ra \(\widehat{ABM} =\widehat{DEN}\) (hai góc tương ứng) hay \(\widehat{ABC} =\widehat{DEF}.\)
Hai tam giác ABC và DEF ta có:
AB = DE (theo giả thiết);
\(\widehat{ABC} =\widehat{DEF}\) (chứng minh trên);
BC = EF (theo giả thiết).
Vậy \(∆ABC = ∆DEF\) (c.g.c).
\(\)
4.30. Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OB = OC = OD như Hình 4.30. Chứng minh ABCD là hình chữ nhật.
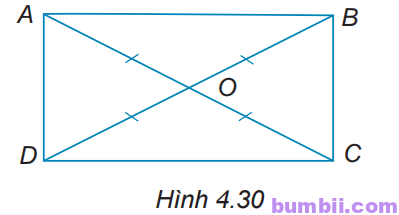
Giải
Hai tam giác OAB và OCD có:
OA = OC (theo giả thiết);
\(\widehat{AOB} =\widehat{COD}\) (hai góc đối đỉnh);
OB = OD (theo giả thiết)
Vậy \(∆OAB = ∆OCD\) (c.g.c).
Suy ra AB = DC và \(\widehat{BAO}=\widehat{OCD}.\)
Mà hai góc này ở vị trí so le trong, do đó AB // DC (1).
Hai tam giác OAD và OCB có:
OA = OC (theo giả thiết);
\(\widehat{AOD} =\widehat{BOC}\) (hai góc đối đỉnh);
OD = OB (theo giả thiết);
Vậy \(∆OAD = ∆OCB\) (c.g.c).
Suy ra AD = BC và \(\widehat{OAD}=\widehat{OCB}.\)
Mà hai góc này ở vị trí so le trong nên AD // BC (2).
Từ (1) và (2) suy ra tứ giác ABCD là hình bình hành.
Ta có: OA = OC = OB = OD, AC = OA + OC, BD = OB + OD.
Do đó, AC = BD.
Hai tam giác ABD và tam giác DCA có:
AB = DC (chứng minh trên)
AD là cạnh chung
BD = AC (chứng minh trên)
Vậy \(∆ABD = ∆DCA\) (c.c.c).
Suy ra \(\widehat{BAD} =\widehat{CDA}\).
Lại có: \(\widehat{BAD} +\widehat{CDA} =180^o \) (do AB // DC, hai góc ở vị trí trong cùng phía)
Do đó: \(\widehat{BAD} =\widehat{CDA} =\displaystyle\frac{180^o}{2}=90^o.\)
Vậy hình bình hành ABCD có một góc vuông nên nó là hình chữ nhật.
\(\)
Xem bài giải trước: Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác
Xem bài giải tiếp theo: Bài 15: Các trường hợp bằng nhau của tam giác vuông
Xem thêm các bài giải khác tại: Giải Bài tập Toán Lớp 7 – NXB Kết Nối Tri Thức Với Cuộc Sống
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech
