Chương 8 – Bài 1: Góc và cạnh của một tam giác trang 46 sách giáo khoa toán lớp 7 tập 2 NXB Chân Trời Sáng Tạo.
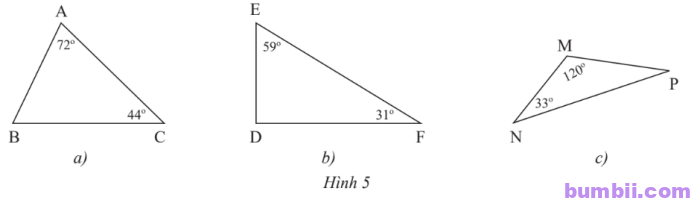
\(1.\) Tìm số đo các góc chưa biết của các tam giác trong Hình \(5\).
Giải
Áp dụng định lí về tổng số đo ba góc của tam giác:
a) Xét tam giác ABC: \(\widehat{B} = 180^o-72^o-44^o = 64^o.\)
b) Xét tam giác DEF: \(\widehat{D} = 180^o-59^o-31^o = 90^o.\)
c) Xét tam giác MNP: \(\widehat{P} = 180^o-120^o-33^o = 27^o.\)
\(\)
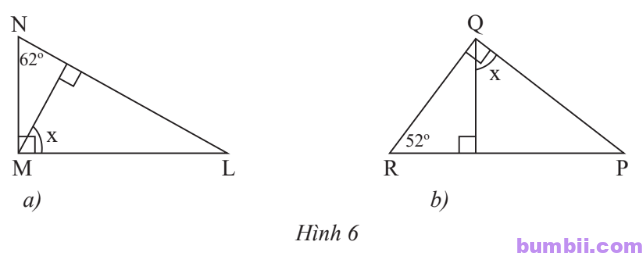
\(2.\) Tính số đo x của góc trong Hình \(6\).
Giải
a)
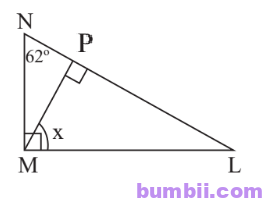
Gọi P là chân vuông góc kẻ từ M xuống cạnh NL.
Áp dụng định lí về tổng số đo ba góc của tam giác:
Xét tam giác MNL vuông tại M: \(\widehat{L} = 180^o-90^o-62^o = 28^o.\)
Xét tam giác MLP vuông tại P: \(\widehat{x} = 180^o-90^o-28^o = 62^o.\)
b)
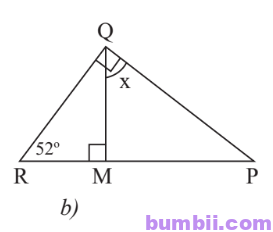
Gọi M là chân vuông góc kẻ từ Q xuống cạnh RP.
Áp dụng định lí về tổng số đo ba góc của tam giác:
Xét tam giác RPQ vuông tại Q: \(\widehat{P} = 180^o-90^o-52^o = 38^o.\)
Xét tam giác QMP vuông tại M: \(\widehat{x} = 180^o-90^o-38^o = 52^o.\)
\(\)
\(3.\) Hãy chia tứ giác ABCD trong Hình 7 thành hai tam giác để tính tổng số đo của bốn góc \(\widehat{A},\ \widehat{B},\ \widehat{C},\ \widehat{D}\).
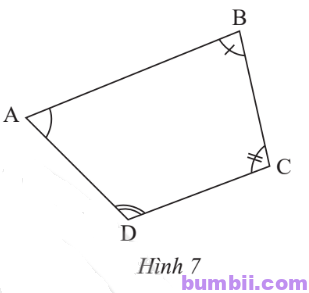
Giải
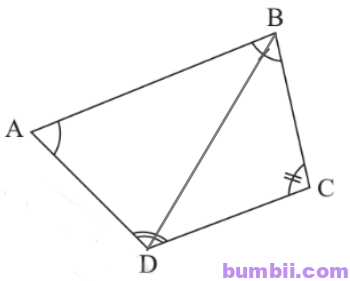
Nối đoạn thẳng BD.
Xét tam giác ABD có: \(\widehat{A} +\widehat{ABD} +\widehat{ADB} =180^o.\)
Xét tam giác BDC có: \(\widehat{C} +\widehat{CBD} +\widehat{CDB} =180^o.\)
Suy ra \(\widehat{A} +\widehat{B} +\widehat{C} +\widehat{D}\)
\(= \widehat{A} +\widehat{ABD} +\widehat{CBD} +\widehat{ADB} +\widehat{CDB} +\widehat{C}
\(=180^o+180^o=360^o.\)
Vậy \(\widehat{A} + \widehat{B} + \widehat{C} + \widehat{D} =360^o.\)
\(\)
\(4.\) Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của một tam giác?
a) \(4\) cm, \(5\) cm, \(7\) cm;
b) \(2\) cm, \(4\) cm, \(6\) cm;
c) \(3\) cm, \(4\) cm, \(8\) cm.
Giải
a) \(5-4 < 7 < 4 + 5\);
b) \(2+ 4 = 6\);
c) \(3 + 4 < 8\).
Vậy chỉ có bộ ba câu a) \(4\) cm, \(5\) cm, \(7\) cm có thể là độ dài ba cạnh của một tam giác vì thỏa mãn bất đẳng thức tam giác.
\(\)
\(5.\) Cho tam giác ABC có BC = \(1\) cm, AB = \(4\) cm. Tính độ dài cạnh AC (theo đơn vị cm), biết rằng độ dài này là một số nguyên.
Giải
Trong tam giác ABC:
AB – BC < AC < AB + BC \(\Rightarrow\) \(3\) < AC < \(5\).
Mà độ dài cạnh AC là một số nguyên nên AC = \(4\) cm.
Vậy AC = \(4\) cm.
\(\)
\(6.\) Trong một trường học, người ta đánh dấu ba khu vực A, B, C là ba đỉnh của một tam giác, biết các khoảng cách AC = \(15\) m, AB = \(45\) m.
a) Nếu đặt ở khu vực C một thiết bị phát wifi có bán kính hoạt động \(30\) m thì tại khu vực B có nhận được tín hiệu không? Vì sao?
b) Cũng câu hỏi như trên với thiết bị phát wifi có bán kính hoạt động \(60\) m.
Giải
a) Ta có CB > AB – AC = \(30\) m suy ra tại khu vực B không nhận được tín hiệu.
b) Ta có CB < AB + AC = \(45\) m < \(60\) m suy ra tại khu vực B nhận được tín hiệu.
\(\)
Xem bài giải trước: Bài tập cuối chương 7
Xem bài giải tiếp theo: Bài 2: Tam giác bằng nhau
Xem thêm các bài giải khác tại: Giải bài tập SGK Toán Lớp 7 – NXB Chân Trời Sáng Tạo.
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech
