Bài 2: Làm quen với xác suất của biến cố ngẫu nhiên

Chương 9 – Bài 2: Làm quen với xác suất của biến cố ngẫu nhiên trang 93 sách giáo khoa toán lớp 7 tập 2 NXB Chân Trời Sáng Tạo.

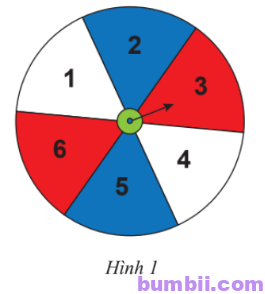
\(1.\) Một tấm bìa hình tròn được chia thành \(6\) phần bằng nhau như Hình \(1\). Bạn Minh đặt tấm bìa nằm thẳng trên bàn, quay mũi tên ở tâm và quan sát xem khi dừng lại thì mũi tên chỉ vào ô nào.

Hãy so sánh xác suất xảy ra của các biến cố sau:

A: “Mũi tên chỉ vào ô có màu đỏ”;

B: “Mũi tên chỉ vào ô ghi số \(3\)”;

C: “Mũi tên chỉ vào ô ghi số lớn hơn \(2\)”.

Giải

Do hình tròn được chia làm \(6\) phần bằng nhau nên mỗi ô đều có cùng khả năng được chọn.

Số ô có màu đỏ lại lớn hơn số ô có ghi số \(3\).

=> P(A) > P(B).

Số ô ghi số lớn hơn \(2\) nhiều hơn số ô có màu đỏ.

=> P(C) > P(A).

Vậy P(C) > P(A) > P(C).

\(\)

\(2.\) Một hộp có chứa \(100\) chiếc thẻ cùng loại, trong đó chỉ có \(1\) thẻ được đánh dấu là Thẻ may mắn. Bình lấy ra ngẫu nhiên \(1\) thẻ. Tính xác suất của biến cố “Thẻ lấy ra là Thẻ may mắn”.

Giải

Chỉ có \(1\) khả năng trong \(100\) khả năng lấy được Thẻ may mắn nên xác suất của biến cố trên bằng \(\displaystyle\frac{1}{100}\).

\(\)

\(3.\) Gieo một con xúc xắc cân đối. Tính xác suất của các biến cố sau:

a) A: “Gieo được mặt có số chấm bằng \(4\)”.

b) B: “Gieo được mặt có số chấm chia hết cho \(5\)”.

c) C: “Gieo được mặt có số chấm là số tròn chục”.

Giải

Khi gieo một con xúc xắc cân đối thì \(6\) mặt của nó có khả năng xuất hiện bằng nhau nên xác suất xuất hiện của mỗi mặt đều là \(\displaystyle\frac{1}{6}\).

a) Do 6 kết quả đều có khả năng xảy ra bằng nhau nên P(A) = \(\displaystyle\frac{1}{6}\).

b) Mặt chia hết cho \(5\) chỉ có một mặt \(5\) chấm nên P(B) = \(\displaystyle\frac{1}{6}\).

c) Biến cố C là biến cố không thể nên P(C) = \(0\).

\(\)

\(4.\) Đội múa có \(1\) bạn nam và \(5\) bạn nữ. Chọn ngẫu nhiên \(1\) bạn để phỏng vấn. Biết mỗi bạn đều có cùng khả năng được chọn. Hãy tính xác suất của biến cố bạn được chọn là nam.

Giải

Do có \(6\) cách chọn ra \(1\) bạn và mỗi bạn đều có cùng khả năng được chọn nên xác suất của biến cố bạn được chọn là nam bằng \(\displaystyle\frac{1}{6}\).

\(\)

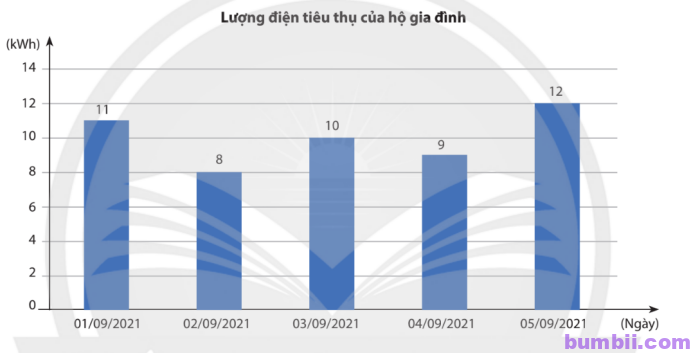
\(5.\) Lượng điện tiêu thụ mỗi ngày trong \(5\) ngày đầu tháng \(9/2021\) của một hộ gia đình được cho ở biểu đồ sau. Chọn ngẫu nhiên \(1\) ngày trong \(5\) ngày đó. Hãy tính xác suất của biến cố “Hộ gia đình sử dụng \(10\) kWh điện trong ngày được chọn”.