Bài tập cuối chương \(IX\) trang \(73\) SGK toán lớp \(10\) tập \(2\) Nhà xuất bản Chân trời sáng tạo. Các em cùng Bumbii giải các bài tập sau.
Bài \(1\). Trong mặt phẳng \(Oxy\), cho bốn điểm \(A(2; 1), B(1; 4), C(4; 5), D(5; 2)\).
\(a)\) Chứng minh \(ABCD\) là một hình vuông.
\(b)\) Tìm toạ độ tâm \(I\) của hình vuông \(ABCD\).
Trả lời:
Ta có: \(\overrightarrow{AB} = (\ – \ 1; 3), \overrightarrow{BC} = (3; 1), \overrightarrow{CD} = (1; \ – \ 3), \overrightarrow{DA} = (3; 1)\).
Suy ra \(AB = BC = CD = DA = \sqrt{10}\)
Lại có: \(\overrightarrow{AB}. \overrightarrow{BC} = (\ – \ 1). 3 + 3. 1 = 0\)
\(\Rightarrow AB \perp BC\)
\(ABCD\) có \(4\) cạnh \(AB = BC = CD = DA\) và \(AB \perp CD\) nên \(ABCD\) là hình vuông (đpcm)
\(b)\) Gọi \(I(x_I; y_I)\) là tâm hình vuông \(ABCD\)
\(\Rightarrow\) \(I\) là trung điểm đường chéo \(AC\)
Suy ra: \(x_I = \displaystyle \frac{2 + 4}{2} = 3\)
\(y_I = \displaystyle \frac{1 + 5}{2} = 3\)
\(\Rightarrow I(3; 3)\)
Vậy toạ độ tâm \(I\) của hình vuông \(ABCD\) là \(I(3; 3)\).
\(\)
Bài \(2\). Cho \(AB\) và \(CD\) là hai dây cung vuông góc tại \(E\) của đường tròn \((O)\). Vẽ hình chữ nhật \(AECF\). Dùng phương pháp toạ độ để chứng minh \(EF\) vuông góc với \(DB\).
Trả lời:
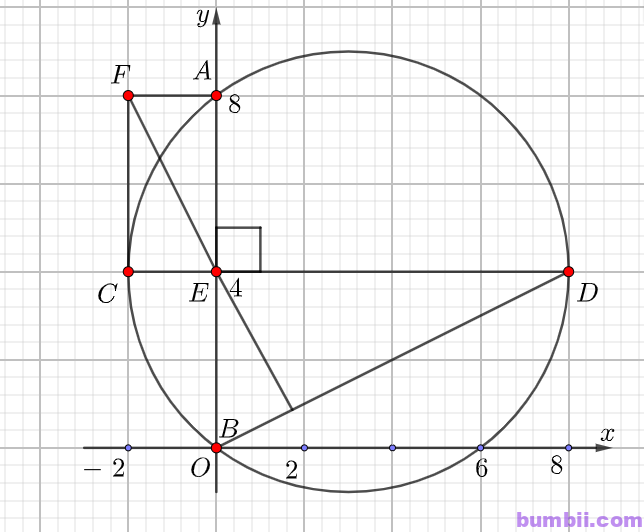
Xét với đường tròn \((C)\) có phương trình:
\((x \ – \ 3)^2 + (y \ – \ 4)^2 = 25\)
Các điểm \(A, B, C, D\) thoả mãn điều kiện bài cho có toạ độ lần lượt là: \(A(8; 0); B(0; 0); C(\ – \ 2; 4); D(8; 4)\)
Ta có phương trình đường thẳng đi qua hai điểm \(A\) và \(B\) là: \(x = 0\)
Phương trình đường thẳng đi qua hai điểm \(C\) và \(D\) là: \(y = 4\)
Lại có \(AB\) và \(CD\) vuông góc với nhau tại \(E\). Nên toạ độ điểm \(E\) thoả mãn hệ phương trình:
\(\left \{\begin{matrix}x = 0\\y = 4 \end{matrix} \right.\)
\(\Rightarrow E(0; 4)\)
Gọi toạ độ điểm \(F\) là \(F(x_F; y_F)\)
\(AECF\) là hình chữ nhật nên \(\overrightarrow{AF} = \overrightarrow{EC}\)
\(\Leftrightarrow (x_F; y_F) = (2; 0)\)
\(\Leftrightarrow F(2; 0)\)
Suy ra: \(\overrightarrow{EF} = 2; \ – \ 4); \overrightarrow{DB} = (8; 4)\)
\(\Rightarrow \overrightarrow{EF}. \overrightarrow{DB} = 2. 8 + (\ – \ 4). 4 = 0\)
\(\Rightarrow \overrightarrow{EF} \perp \overrightarrow{DB}\)
Vậy \(\overrightarrow{EF} \perp \overrightarrow{DB}\) (đpcm)
\(\)
Bài \(3\). Tìm toạ độ giao điểm và góc giữa hai đường thẳng \(d_1\) và \(d_2\) trong mỗi trường hợp sau:
\(a)\) \(d_1: x \ – \ y + 2 = 0\) và \(d_2: x + y + 4 = 0\);
\(b)\) \(d_1: \left \{\begin{matrix}x = 1 + t\\y = 3 + 2t \end{matrix} \right.\) và \(d_2: x \ – \ 3y + 2 = 0\);
\(c)\) \(d_1: \left \{\begin{matrix}x = 2 \ – \ t\\y = 5 + 3t \end{matrix} \right.\) và \(d_2: \left \{\begin{matrix}x = 1 + 3t’\\y = 3 + t’ \end{matrix} \right.\).
Trả lời:
\(a)\) Gọi \(A(x_A; y_A)\) là giao điểm của \(d_1\) và \(d_2\)
Khi đó toạ độ điểm \(A\) thoả mãn hệ phương trình:
\(\left \{\begin{matrix}x \ – \ y + 2 = 0\\x + y + 4 = 0 \end{matrix} \right.\)
\(\Leftrightarrow \left \{\begin{matrix}x \ – \ y = \ – \ 2\\x + y = \ – \ 4 \end{matrix} \right.\)
\(\Leftrightarrow \left \{\begin{matrix}2x = \ – \ 6\\x + y = \ – \ 4 \end{matrix} \right.\)
\(\Leftrightarrow \left \{\begin{matrix}x = \ – \ 3\\y = \ – \ 1 \end{matrix} \right.\)
\(\Rightarrow A(\ – \ 3; \ – \ 1)\)
Ta có:
\(d_1\) có vectơ pháp tuyến \(\overrightarrow{n_1} = (1; \ – \ 1)\)
\(d_2\) có vectơ pháp tuyến \(\overrightarrow{n_2} = (1; 1)\)
Ta thấy \(\overrightarrow{n_1}. \overrightarrow{n_2} = 1. 1 + (\ – \ 1). 1 = 0\)
Suy ra \(\overrightarrow{n_1} \perp \overrightarrow{n_2}\) hay \((\overrightarrow{n_1}; \overrightarrow{n_2}) = 90^o\)
\(\Rightarrow (d_1; d_2) = 90^o\)
Vậy giao điểm của hai đường thẳng \(d_1\) và \(d_2\) là \(A(\ – \ 3; \ – \ 1)\) và góc giữa hai đường thẳng là \(90^o\).
\(b)\) \(d_1\) có vectơ chỉ phương \(\overrightarrow{u_1} = (1; 2)\) nên có vectơ pháp tuyến \(\overrightarrow{n_1} = (2; \ – \ 1)\)
\(d_2\) đi qua điểm \((1; 3)\) và có vectơ pháp tuyến \(\overrightarrow{n_2} = (2; \ – \ 1)\) nên \(d_2\) có phương trình: \(2(x \ – \ 1) \ – \ 1(y \ – \ 3) = 0\)
\(\Leftrightarrow 2x \ – \ y + 1 = 0\)
\(\Rightarrow d_2\) có vectơ pháp tuyến \(\overrightarrow{n_2} = (2; \ – \ 1)\)
Gọi \(B(x_B; y_B)\) là giao điểm của \(d_1\) và \(d_2\)
\(\Rightarrow\) Toạ độ điểm \(B\) thoả mãn hệ phương trình:
\(\left \{\begin{matrix}2x \ – \ y + 1 = 0\\x \ – \ 3y + 2 = 0 \end{matrix} \right.\)
\(\Leftrightarrow \left \{\begin{matrix}2x \ – \ y = \ – \ 1\\x \ – \ 3y = \ – \ 2 \end{matrix} \right.\)
\(\Leftrightarrow \left \{\begin{matrix}2x \ – \ y = \ – \ 1\\2x \ – \ 6y = \ – \ 3 \end{matrix} \right.\)
\(\Leftrightarrow \left \{\begin{matrix}5y = 3\\2x \ – \ y = \ – \ 1 \end{matrix} \right.\)
\(\Leftrightarrow \left \{\begin{matrix}y = \displaystyle \frac{3}{5}\\x = \displaystyle \frac{1}{5} \end{matrix} \right.\)
\(\Rightarrow B\left(\displaystyle \frac{1}{5}; \displaystyle \frac{3}{5} \right)\)
Áp dụng công thức tính góc giữa hai đường thẳng ta có:
\(\cos(d_1; d_2) = |\cos{(\overrightarrow{n_1}; \overrightarrow{n_2})}| \)
\(= \displaystyle \frac{|2. 1 + (\ – \ 1). (\ – \ 3)|}{\sqrt{2^2 + (\ – \ 1)^2}. \sqrt{1^2 + (\ – \ 3)^2}}\)
\(= \displaystyle \frac{5}{\sqrt{5}. \sqrt{10}} = \displaystyle \frac{\sqrt{2}}{2}\)
\(\Rightarrow (d_1; d_2) = 45^o\)
Vậy giao điểm của hai đường thẳng \(d_1\) và \(d_2\) là \(B\left(\displaystyle \frac{1}{5}; \displaystyle \frac{3}{5} \right)\) và góc giữa hai đường thẳng là \(45^o\).
\(c)\) Gọi \(C(x_C; y_C)\) là giao điểm của \(d_1\) và \(d_2\)
Khi đó toạ độ điểm \(C\) thoả mãn hệ phương trình:
\(\left \{\begin{matrix}2 \ – \ t = 1 + 3t’\\5 + 3t = 3 + t’ \end{matrix} \right.\)
\(\Leftrightarrow \left \{\begin{matrix}t = 1 \ – \ 3t’\\5 + 3(1 \ – \ 3t’) = 3 + t’ \end{matrix} \right.\)
\(\Leftrightarrow \left \{\begin{matrix}t = 1 \ – \ 3t’\\t’ = \displaystyle \frac{1}{2} \end{matrix} \right.\)
\(\Leftrightarrow \left \{\begin{matrix}t = \ – \ \displaystyle \frac{1}{2}\\t’ =\displaystyle \frac{1}{2} \end{matrix} \right.\)
Suy ra \(x_C = 2 \ – \ (\ – \ \displaystyle \frac{1}{2}) = \displaystyle \frac{5}{2}\)
\(y_C = 5 + 3. \displaystyle \frac{1}{2} = 5 + 3. (\ – \ \displaystyle \frac{1}{2}) = \displaystyle \frac{7}{2}\)
\(\Rightarrow C\left(\displaystyle \frac{5}{2}; \displaystyle \frac{7}{2}\right)\)
\(d_1\) có vectơ chỉ phương \(\overrightarrow{u_1} = (\ – \ 1; 3)\)
\(d_2\) có vectơ chỉ phương \(\overrightarrow{u_2} = (3; 1)\)
Ta có: \(\overrightarrow{u_1}. \overrightarrow{u_2} = (\ – \ 1). 3 + 3. 1 = 0\)
\(\Rightarrow \overrightarrow{u_1} \perp \overrightarrow{u_2}\) Hay (\overrightarrow{u_1}; \overrightarrow{u_2} = 90^o\)
Suy ra \((d_1; d_2) = 90^o\)
Vậy giao điểm của hai đường thẳng \(d_1\) và \(d_2\) là \(C\left(\displaystyle \frac{5}{2}; \displaystyle \frac{7}{2} \right)\) và góc giữa hai đường thẳng là \(90^o\).
\(\)
Bài \(4\). Tính bán kính của đường tròn tâm \(M(\ – \ 2; 3)\) và tiếp xúc với đường thẳng \(d: 14x \ – \ 5y + 60 = 0\).
Trả lời:
Đường tròn tâm \(M\) tiếp xúc với đường thẳng \(d: 14x \ – \ 5y + 60 = 0\) nên khoảng cách từ tâm \(M\) đến \(d\) chính là bán kính đường tròn.
Ta có:
\(R = d(M, d) = \displaystyle \frac{|14. (\ – \ 2) \ – \ 5. 3 + 60|}{\sqrt{14^2 +(\ – \ 5)^2}} = \displaystyle \frac{\sqrt{221}}{13}\)
Vậy bán kính đường tròn cần tìm là \(\displaystyle \frac{\sqrt{221}}{13}\)
\(\)
Bài \(5\). Tính khoảng cách giữa hai đường thẳng: \(\Delta: 6x + 8y \ – \ 13 = 0\) và \(\Delta’: 3x + 4y \ – \ 27 = 0\).
Trả lời:
Đường thẳng \(\Delta\) có vectơ pháp tuyến \(\overrightarrow{n_1} = (6; 8)\)
Đường thẳng \(\Delta’\) có vectơ pháp tuyến \(\overrightarrow{n_2} = (3; 4)\)
Ta có: \(\overrightarrow{n_1} = 2. \overrightarrow{n_2}\)
\(\Rightarrow \overrightarrow{n_1}\) và \(\overrightarrow{n_2}\) cùng phương
\(\Rightarrow\) Hai đường thẳng \(\Delta\) và \(\Delta’\) song song với nhau.
Lấy điểm \(M(1; 6) \in \Delta’\). Ta tính khoảng cách từ \(M\) đến \(\Delta\)
Áp dụng công thức tính khoảng cách từ điểm đến đường thẳng ta được:
\(d(M; \Delta) = \displaystyle \frac{|6. 1 + 8. 6 \ – \ 13|}{\sqrt{6^2 + 8^2}}= 4,1\)
Vậy khoảng cách giữa hai đường thẳng \(\Delta\) và \(\Delta’\) bằng khoảng cách từ điểm \(M \in \Delta’\) đến \(\Delta\) và bằng \(4,1\)
\(\)
Bài \(6\). Tìm tâm và bán kính của các đường tròn có phương trình:
\(a)\) \((x \ – \ 2)^2 + (y \ – \ 7)^2 = 64\);
\(b)\) \((x + 3)^2 + (y + 2)^2 = 8\);
\(c)\) \(x^2 + y^2 \ – \ 4x \ – \ 6y \ – \ 12 = 0\).
Trả lời:
\(a)\) Xét phương trình \((x \ – \ 2)^2 + (y \ – \ 7)^2 = 64\) có tâm \((2; 7)\) và bán kính \(R = \sqrt{64} = 8\)
Vậy đường tròn đã cho có tâm \((2; 7)\) và bán kính bằng \(8\).
\(b)\) Xét phương trình \((x + 3)^2 + (y + 2)^2 = 8\) có tâm \((\ – \ 3; \ – \ 2)\) và bán kính \(R = \sqrt{8} = 2\sqrt{2}\)
Vậy đường tròn đã cho có tâm \((\ – \ 3; \ – \ 2)\) và bán kính bằng \(2\sqrt{2}\).
\(c)\) Xét phương trình \(x^2 + y^2 \ – \ 4x \ – \ 6y \ – \ 12 = 0\)
\(\Rightarrow x^2 \ – \ 4x + 4 + y^2 \ – \ 6y + 9 = 25\)
\(\Rightarrow (x \ – \ 2)^2 + (y \ – \ 3)^2 = 5^2\)
Vậy đường tròn đã cho có tâm \((2; 3)\) và bán kính bằng \(5\).
\(\)
Bài \(7\). Lập phương trình đường tròn trong các trường hợp sau:
\(a)\) Có tâm \(I(\ – \ 2; 4)\) và bán kính bằng \(9\);
\(b)\) Có tâm \((I(1; 2)\) và đi qua điểm \(A(4; 5)\);
\(c)\) Đi qua hai điểm \((A(4; 1), B(6; 5)\) và có tâm nằm trên đường thẳng \(4x + y \ – \ 16 = 0\);
\(d)\) Đi qua gốc toạ độ và cắt hai trục toạ độ tại các điểm có hoành độ là \(a\), tung độ là \(b\).
Trả lời:
\(a)\) Phương trình đường tròn tâm \(I(\ – \ 2; 4\)\) và bán kính \(R = 9\) là:
\((x + 2)^2 + (y \ – \ 4)^2 = 9^2\)
Vậy phương trình đường tròn cần tìm là \((x + 2)^2 + (y \ – \ 4)^2 = 81\)
\(b)\) Ta có: \(\overrightarrow{IA} = (3; 3)\)
\(\Rightarrow R = IA = |\overrightarrow{IA}| = \sqrt{3^2 + 3^2} = 3\sqrt{2}\)
Phương trình đường tròn tâm \(I(1; 2)\) và có bán kính \(R = 3\sqrt{2}\) là:
\((x \ – \ 1)^2 + (y \ – \ 2)^2 = (3\sqrt{2})^2\)
\(\Leftrightarrow (x \ – \ 1)^2 + (y \ – \ 2)^2 = 18\)
Vậy phương trình đường tròn cần tìm là \((x \ – \ 1)^2 + (y \ – \ 2)^2 = 18\).
\(c)\) Đường tròn có tâm nằm trên đường thẳng \(4x + y \ – \ 16 = 0\) nên toạ độ tâm \(I\) của đường tròn là: \(I(x; 16 \ – \ 4x)\).
Suy ra:
\(\overrightarrow{IA} = (x \ – \ 4; 15 \ – \ 4x)\)
\(\overrightarrow{IB} = (x \ – \ 6; 11 \ – \ 4x)\)
\(\Rightarrow IA = \sqrt{(x \ – \ 4)^2 + (15 \ – \ 4x)^2}; IB = \sqrt{(x \ – \ 6)^2 + (11 \ – \ 4x)^2}\)
Mà \(A, B \in\) đường tròn nên \(IA = IB = R\)
\(\Rightarrow \sqrt{(x \ – \ 4)^2 + (15 \ – \ 4x)^2} = \sqrt{(x \ – \ 6)^2 + (11 \ – \ 4x)^2}\)
\(\Rightarrow (x \ – \ 4)^2 + (15 \ – \ 4x)^2 = (x \ – \ 6)^2 + (11 \ – \ 4x)^2\)
\(\Rightarrow 17x^2 \ – \ 128x + 241 = 17x^2 \ – \ 100x + 157\)
\(\rightarrow \ – \ 28x = 84\)
\(\Rightarrow x = 3\)
\(\Rightarrow I(3; 4); R = IA = \sqrt{10}\)
Phương trình đường tròn tâm \(I(3; 4)\) và có bán kính \(R = \sqrt{10}\) là:
\((x \ – \ 3)^2 + (y \ – \ 4)^2 = 10\)
\(d)\) Gọi phương trình đường tròn có dạng:
\(x^2 + y^2 \ – \ 2mx \ – \ 2ny + p = 0\) với tâm \(I(m; n)\) và bán kính \(R = \sqrt{m^2 + n^2 \ – \ p}\)
Đường tròn đi qua gốc toạ độ và cắt hai trục toạ độ tại các điểm có hoành độ \(a\) và tung độ \(b\) nên \(a\) và \(b \neq 0\). Ta có hệ phương trình:
\(\left \{\begin{matrix}0^2 + 0^2 \ – \ 2. m. 0 \ – \ 2. n. 0 + p = 0\\a^2 + 0^2 \ – \ 2. m . a \ – \ 2. n. 0 + p = 0\\0^2 + b^2 \ – \ 2. m. 0 \ – \ 2. n. b + p = 0 \end{matrix} \right.\)
\(\Rightarrow \left \{\begin{matrix}p = 0\\a^2 \ – \ 2. m. a = 0\\b^2 \ – \ 2. n. b = 0 \end{matrix} \right.\)
\(\Rightarrow \left \{\begin{matrix}p = 0\\m = \displaystyle \frac{a}{2}\\n = \displaystyle \frac{b}{2} \end{matrix} \right.\)
Vậy phương trình đường tròn cần tìm là:
\(x^2 + y^2 \ – \ ax \ – \ by = 0\)
\(\)
Bài \(8\). Viết phương trình tiếp tuyến của đường tròn \((C)\): \((x + 5)^2 + (y \ – \ 3)^2 = 1000\) tại điểm \(M(11; 11)\).
Trả lời:
Xét đường tròn \((C)\): \((x + 5)^2 + (y \ – \ 3)^2 = 100\) có tâm \(I(\ – \ 5; 3)\) và có bán kính \(R = 10\sqrt{10}\)
Ta có: \(\overrightarrow{IM} = (6; 8)\)
Phương trình tiếp tuyến của đường tròn \((C)\) tại điểm \(M(11; 11)\) là:
\(6(x \ – \ 11) + 8(y \ – \ 11) = 0\)
\(\Leftrightarrow 6x + 8y \ – \ 154 = 0\)
\(\Leftrightarrow 3x + 4y \ – \ 77 = 0\)
Vậy phương trình tiếp tuyến của đường tròn \((C)\) cần tìm là: \(3x + 4y \ – \ 77 = 0\).
\(\)
Bài \(9\). Tìm toạ độ các tiêu điểm, toạ độ các đỉnh, độ dài trục lớn và trục nhỏ của các elip sau:
\(a)\) \(\displaystyle \frac{x^2}{100} + \displaystyle \frac{y^2}{36} = 1\);
\(b)\) \(\displaystyle \frac{x^2}{25} + \displaystyle \frac{y^2}{16} = 1\);
\(c)\) \(x^2 + 16y^2 = 16\).
Trả lời:
\(a)\) Ta có: \(\displaystyle \frac{x^2}{100} + \displaystyle \frac{y^2}{36} = 1\)
\(\Leftrightarrow \displaystyle \frac{x^2}{10^2} + \displaystyle \frac{y^2}{6^2} = 1\)
Đây là phương trình elip với \(a = 10; b = 6\)
\(\Rightarrow c = \sqrt{a^2 \ – \ b^2} = \sqrt{100 \ – \ 36} = 8\)
Toạ độ các tiêu điểm là \(F_1(\ – \ 8; 0); F_2(8; 0)\)
Toạ độ các đỉnh là \(A_1 (\ – \ 10; 0); A_2(10; 0); B_1(0; \ – \ 6); B_2(0; 6)\)
Độ dài trục lớn \(2a = 2. 10 = 20\)
Độ dài trục nhỏ \(2b = 2. 6 = 12\)
\(b)\) Ta có \(\displaystyle \frac{x^2}{25} + \displaystyle \frac{y^2}{16} = 1\)
\(\Leftrightarrow \displaystyle \frac{x^2}{5^2} + \displaystyle \frac{y^2}{4^2}\)
Đây là phương trình elip với \(a = 5; b = 4\)
\(\Rightarrow c = \sqrt{5^2 \ – \ 4^2} = \sqrt{9} = 3\)
Toạ độ các tiêu điểm là \(F_1(\ – \ 3; 0); F_2(3; 0)\)
Toạ độ các đỉnh là \(A_1 (\ – \ 5; 0); A_2(5; 0); B_1(0; \ – \ 4); B_2(0; 4)\)
Độ dài trục lớn \(2a = 2. 5 = 10\)
Độ dài trục nhỏ \(2b = 2. 4 = 8\)
\(c)\) \(x^2 + 16y^2 = 16\)
\(\Leftrightarrow \displaystyle \frac{x^2}{16} + \displaystyle \frac{16y^2}{16} = 1\)
\(\Leftrightarrow{x^2}{4^2} + \displaystyle \frac{y^2}{1^2} = 1\)
Đây là phương trình elip với \(a = 4; b = 1\)
\(\Rightarrow c = \sqrt{4^2 \ – \ 1^2} = \sqrt{15}\)
Toạ độ các tiêu điểm là:\(F_1(\ – \ \sqrt{15}; 0); F_2(\sqrt{15}; 0)\)
Toạ độ các đỉnh là \(A_1(\ – \ 4; 0); A_2(4; 0); B_1(0; \ – \ 1); B_2(0; 1)\)
Độ dài trục lớn \(2a = 2. 4 = 8\)
Độ dài trục nhỏ là \(2b = 2. 1 = 2\).
\(\)
Bài \(10\). Viết phương trình chính tắc của elip thoả mãn từng điều kiện:
\(a)\) Đỉnh \((5; 0), (0; 4)\);
\(b)\) Đỉnh \((5; 0)\), tiêu điểm \((3; 0)\);
\(c)\) Độ dài trục lớn \(16\), độ dài trục nhỏ \(12\);
\(d)\) Độ dài trục lớn \(20\), tiêu cự \(12\).
Trả lời:
\(a)\) Đỉnh của elip là \(5; 0), (0; 4)\) nên \(a = 5; b = 4\)
Phương trình chính tắc của elip cần tìm là:
\(\displaystyle \frac{x^2}{5^2} + \displaystyle \frac{y^2}{4^2} = 1\)
\(\Leftrightarrow \displaystyle \frac{x^2}{25} + \displaystyle \frac{y^2}{16} = 1\)
\(b)\) Đỉnh của elip \((5; 0)\) suy ra \(a = 5\)
Tiêu điểm \((3; 0)\) suy ra \(c = 3\)
\(\Rightarrow b = \sqrt{a^2 \ – \ c^2} = \sqrt{5^2 \ – \ 3^2} = 4\)
Phương trình chính tắc của elip cần tìm là: \(\displaystyle \frac{x^2}{5^2} + \displaystyle \frac{y^2}{4^2} = 1\)
\(\Leftrightarrow \displaystyle \frac{x^2}{25} + \displaystyle \frac{y^2}{16} = 1\)
\(c)\) Độ dài trục lớn \(16\) nên \(2a = 16\), độ dài trục nhỏ \(12\)
Nên \(2a = 16; 2b = 12\)
\(\Rightarrow a = 8; b = 6\)
Vậy phương trình chính tắc của elip cần tìm là:
\(\displaystyle \frac{x^2}{8^2} + \displaystyle \frac{y^2}{6^2} = 1\)
\(\Leftrightarrow \displaystyle \frac{x^2}{64} + \displaystyle \frac{y^2}{36} = 1\)
\(d)\) Độ dài trục lớn \(20\), tiêu cự \(12\) nên \(2a = 20; 2c = 12\)
\(\Rightarrow a = 10; c = 6\)
\(\Rightarrow b = \sqrt{10^2 \ – \ 6^2} = \sqrt{64} = 8\)
Vậy phương trình chính tắc của elip cần tìm là:
\(\displaystyle \frac{x^2}{10^2} + \displaystyle \frac{y^2}{8^2} = 1\)
\(\Leftrightarrow \displaystyle \frac{x^2}{100} + \displaystyle \frac{y^2}{64} = 1\).
\(\)
Bài \(11\). Tìm toạ độ các tiêu điểm, toạ độ các đỉnh, độ dài trục thực và trục ảo của các hypebol sau:
\(a)\) \(\displaystyle \frac{x^2}{16} \ – \ \displaystyle \frac{y^2}{9} = 1\);
\(b)\) \(\displaystyle \frac{x^2}{64} \ – \ \displaystyle \frac{y^2}{36} = 1\);
\(c)\) \(x^2 \ – \ 16y^2 = 16\);
\(d)\) \(9x^2 \ – \ 16y^2 = 144\).
Trả lời:
\(a)\) Ta có hypebol \(\displaystyle \frac{x^2}{16} \ – \ \displaystyle \frac{y^2}{9} = 1\)
\(\Leftrightarrow \displaystyle \frac{x^2}{4^2} \ – \ \displaystyle \frac{y^2}{3^2} = 1\) có \(a = 4; b = 3\)
\(\Rightarrow c = \sqrt{4^2 + 3^2} = \sqrt{25} = 5\)
Khi đó toạ độ các tiêu điểm là \(F_1(\ – \ 5; 0); F_2(5; 0)\)
Toạ độ các đỉnh \(A_1(\ – \ 4; 0); A_2(4; 0)\)
Độ dài trục thực \(2a = 8\)
Độ dài trục ảo \(2b = 6\)
\(b)\) Xét phương trình \(\displaystyle \frac{x^2}{64} \ – \ \displaystyle \frac{y^2}{36} = 1\)
\(\Leftrightarrow \displaystyle \frac{x^2}{8^2} \ – \ \displaystyle \frac{y^2}{6^2} = 1\) có \(a = 8; b = 6\)
\(\Rightarrow c = \sqrt{8^2 + 6^2} = \sqrt{100} = 10\)
Khi đó toạ độ các tiêu điểm là \(F_1(\ – \ 10; 0); F_2(10; 0)\)
Toạ độ các đỉnh \(A_1(\ – \ 8; 0); A_2(8; 0)\)
Độ dài trục thực \(2a = 16\)
Độ dài trục ảo \(2b = 12\)
\(c)\) Xét phương trình \(x^2 \ – \ 16y^2 = 16\)
\(\Leftrightarrow \displaystyle \frac{x^2}{4^2} \ – \ \displaystyle \frac{y^2}{1^2} = 1\) có \(a = 4; b = 1\)
\(\Rightarrow c = \sqrt{4^2 + 1^2} = \sqrt{17}\)
Khi đó toạ độ các tiêu điểm là \(F_1(\ – \ \sqrt{17}; 0); F_2(\sqrt{17}; 0)\)
Toạ độ các đỉnh \(A_1(\ – \ 4; 0); A_2(4; 0)\)
Độ dài trục thực \(2a = 8\)
Độ dài trục ảo \(2b = 2\)
\(d)\) Xét phương trình \(9x^2 \ – \ 16y^2 = 144\)
\(\Leftrightarrow \displaystyle \frac{x^2}{4^2} \ – \ \displaystyle \frac{y^2}{3^2} = 1\) có \(a = 4; b = 3\)
\(\Rightarrow c = \sqrt{4^2 + 3^2} = 5\)
Khi đó toạ độ các tiêu điểm là \(F_1(\ – \ 5; 0); F_2(5; 0)\)
Toạ độ các đỉnh \(A_1(\ – \ 4; 0); A_2(4; 0)\)
Độ dài trục thực \(2a = 8\)
Độ dài trục ảo \(2b = 6\)
\(\)
Bài \(12\). Viết phương trình chính tắc của hypebol thoả mãn từng điều kiện sau:
\(a)\) Đỉnh \((3; 0)\), tiêu điểm \((5; 0)\);
\(b)\) Độ dài trục thực \(8\), độ dài trục ảo \(6\).
Trả lời:
\(a)\) Đỉnh \((3; 0)\) suy ra \(a = 3\)
Tiêu điểm \((5; 0)\) suy ra \(c = 5\)
\(\Rightarrow b = \sqrt{5^2 \ – \ 3^2} = 4\)
\(\Rightarrow\) Phương tình chính tắc của hypebol là:
\(\displaystyle \frac{x^2}{3^2} \ – \ \displaystyle \frac{y^2}{4^2} = 1\)
\(\Leftrightarrow \displaystyle \frac{x^2}{9} \ – \ \displaystyle \frac{y^2}{16} = 1\)
vậy phương trình chính tắc của hypebol cần tìm là \(\displaystyle \frac{x^2}{9} \ – \ \displaystyle \frac{y^2}{16} = 1\)
\(b)\) Độ dài trục thực \(8\), độ dài trục ảo \(6\)
\(\Rightarrow 2a = 8; 2b = 6\)
\(\Rightarrow a = 4; b = 3\)
\(\Rightarrow\) Phương trình chính tắc của hypebol là:
\(\displaystyle \frac{x^2}{4^2} \ – \ \displaystyle \frac{y^2}{3^2} = 1\)
\(\Leftrightarrow \displaystyle \frac{x^2}{9} \ – \ \displaystyle \frac{y^2}{16} = 1\)
Vậy phương tình chính tắc ủa hypebol cần tìm là: \(\displaystyle \frac{x^2}{9} \ – \ \displaystyle \frac{y^2}{16} = 1\).
\(\)
Bài \(13\). Tìm toạ độ tiêu điểm, phương trình đường chuẩn của các parabol sau:
\(a)\) \(y^2 = 12x\);
\(b)\) \(y^2 = x \).
Trả lời:
\(a)\) Ta có: \(y^2 = 12x = 2. 6. x\)
\(\Rightarrow p = 6\)
Khi đó toạ độ tiêu điểm \(F(\displaystyle \frac{p}{2}; 0) = (3; 0)\);
Phương trình đường chuẩn là \(x + 3 = 0\)
\(b)\) \(y^2 = x = 2. \displaystyle \frac{1}{2}. x\)
\(\Rightarrow p = \displaystyle \frac{1}{2}\)
Khi đó:
Toạ độ tiêu điểm \(F\left(\displaystyle \frac{p}{2}; 0 \right) = \left(\displaystyle \frac{1}{4}; 0 \right)\)
Phương trình đường chuẩn là: \(x + \displaystyle \frac{1}{4} = 0\)
\(\)
Bài \(14\). Viết phương trình chính tắc của parabol thoả mãn từng điều kiện sau:
\(a)\) Tiêu điểm \((4; 0)\);
\(b)\) Đường chuẩn có phương trình \(x = \ – \ \displaystyle \frac{1}{6}\);
\(c)\) Đi qua điểm \((1; 4)\);
\(d)\) Khoảng cách từ tiêu điểm đến đường chuẩn bằng \(8\).
Trả lời:
\(a)\) Tiêu điểm \(F(4; 0)\) nên \(\displaystyle \frac{p}{2} = 4\)
\(\Rightarrow p = 8\)
Suy ra phương trình chính tắc của parabol là:
\(y^2 = 2px = 16x\)
\(b)\) Đường chuẩn có phương trình \(x = \ – \ \displaystyle \frac{1}{6}\)
\(\Leftrightarrow x + \displaystyle \frac{1}{6} = 0\)
\(\Rightarrow \displaystyle \frac{p}{2} = \displaystyle \frac{1}{6}\)
\(\Rightarrow p = \displaystyle \frac{1}{3}\)
Suy ra phương trình chính tắc của parabol là:
\(y^2 = 2px = \displaystyle \frac{2}{3}.x\)
\(c)\) Gọi phương trình chính tắc của parabol cần tìm là \(y^2 = 2px\)
Parabol đi qua điểm \((1; 4)\) nên ta có:
\(4^2 = 2. p. 1\)
\(\Rightarrow p = 8\)
Suy ra phương trình chính tắc của parabol là: \(y^2 = 2px = 16x\)
\(d)\) Gọi tiêu điểm \(F\left(\displaystyle \frac{p}{2}; 0 \right)\) và đường chuẩn của parabol cần tìm là \(\Delta: x + \displaystyle \frac{p}{2} = 0\)
Áp dụng công thức tính khoảng cách từ điểm đến đường thẳng ta có:
\(d(F; \Delta) = \displaystyle \frac{|\displaystyle \frac{p}{2} + \displaystyle \frac{p}{2}|}{\sqrt{1^2 + 0^2}} = |p| = p\)
Theo bài ra khoảng cách từ tiêu điểm đến đường chuẩn bằng \(8\) nên \(p = 8\).
Suy ra phương trình chính tắc của parabol cần tìm là \(y^2 = 2px = 16x\)
\(\)
Bài \(15\). Một gương lõm có mặt cắt hình parabol như Hình \(1\), có tiêu điểm cách đỉnh \(5 cm\). Cho biết bề sâu của gương là \(45 cm\), tính khoảng cách \(AB\).
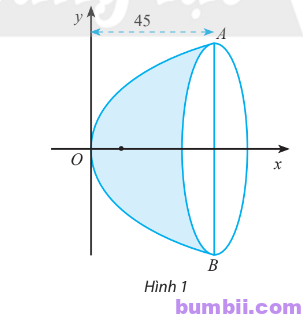
Trả lời:
Parabol có tiêu điểm cách đỉnh \(5 cm\) nên \(\displaystyle \frac{p}{2} = 5\)
\(\Rightarrow p = 10\)
Phương trình chính tắc của parabol là:
\(y^2 = 2px = 20x\)
Gọi toạ độ điểm \(A\) là \(A(x_A; y_A)\)
Do bề sâu của gương là \(45 cm\) nên \(x_A = 45\)
\(\Rightarrow y_A^2 = 20. 45 = 900\)
\(\Rightarrow y_A = 30\)
Khoảng cách \(AB\) bằng hai lần khoảng cách từ \(A\) đến trục \(Ox\) và bằng: \(2. 30 = 60 (cm)\)
Vậy khoảng cách \(AB\) bằng \(60 cm \)
\(\)
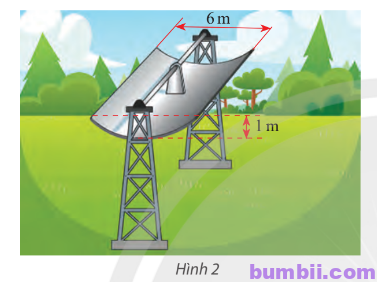
Bài \(16\). Một bộ thu năng lượng mặt trời để làm nóng nước được làm bằng một tấm thép không gỉ có mặt cắt hình parabol (Hình \(2\)). Nước sẽ chảy thông qua một đường ống nằm ở tiêu điểm của parabol.
\(a)\) Viết phương trình chính tắc của parabol.
\(b)\) Tính khoảng cách từ tâm đường ống đến đỉnh của parabol.
Trả lời:
Ta đặt hệ trục toạ độ như hình dưới:
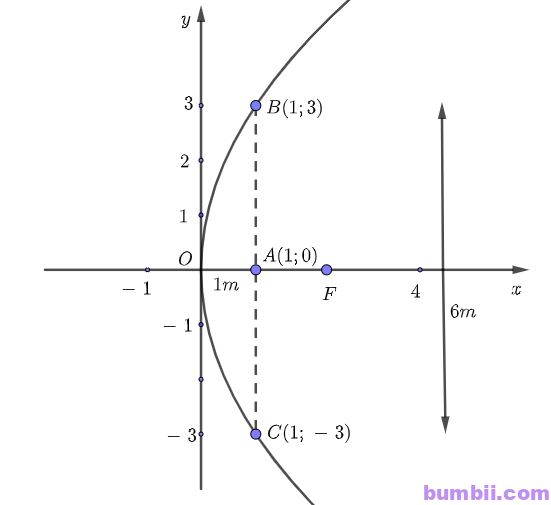
\(a)\) Theo hình vẽ, điểm \(B(1; 3)\) thuộc parabol nên toạ độ điểm \(A\) thoả mãn:
\(3^2 = 2. p. 1 \)
\(\Leftrightarrow p = \displaystyle \frac{9}{2}\)
Khi đó phương trình chính tắc của parabol là:
\(y^2 = 2px = 2. \displaystyle \frac{9}{2}. x = 9x\)
\(b)\) Tâm của đường ống chính là tiêu điểm của parabol.
Khi đó ta có toạ độ tiêu điểm \(F\left(\displaystyle \frac{p}{2}; 0 \right) = \left(\displaystyle \frac{9}{4}; 0 \right)\)
Vậy khoảng cách từ tâm đường ống đến đỉnh của parabol là \(\displaystyle \frac{9}{4} m\)
\(\)
Bài \(17\). Cổng chào của một thành phố dạng hình parabol có khoảng cách giữa hai chân cổng là \(192 m\) (Hình \(3\)). Từ một điểm \(M\) trên thân cổng, người ta đo được khoảng cách đến mặt đất là \(2 m\) và khoảng cách từ chân đường vuông góc vẽ từ \(M\) xuống mặt đất đến chân cổng gần nhất là \(0,5 m\). Tính chiều cao của cổng.
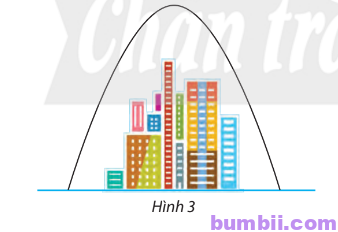
Trả lời:
Gắn hệ trục toạ độ \(Oxy\) vào cổng, ta vẽ lại được parabol như dưới đây:
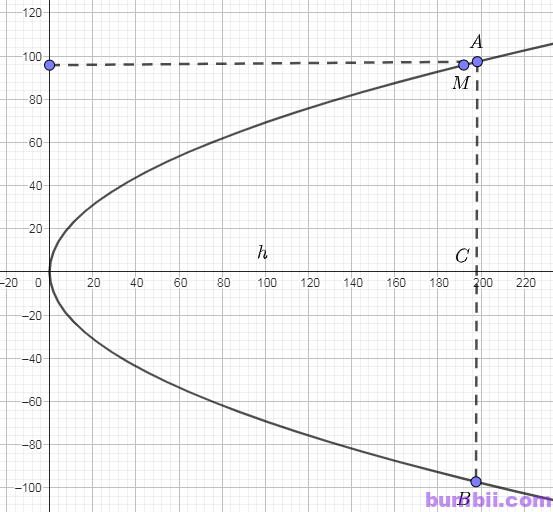
Gọi phương tình mô phỏng parabol có dạng: \(y^2 = 2px\)
Theo bài ra ta có:
\(AB = 2. y_A = 192\)
\(\Rightarrow y_A = 96\)
Gọi chiều cao của cổng là \(OC = h\)
Suy ta toạ độ điểm \(M\) là \(M(h \ – \ 2; 96 \ – \ 0,5) = (h \ – \ 2; 95,5)\)
Toạ độ điểm \(A\) là \(A(h; 96)\)
Hai điểm \(A\) và \(M\) thuộc parabol nên ta có hệ phương trình sau:
\(\left \{\begin{matrix}96^2 = 2ph\\95,5^2 = 2p(h \ – \ 2) \end{matrix} \right.\)
\(\Leftrightarrow \left \{\begin{matrix}96^2 = 2ph\\95,5^2 = 2ph \ – \ 4p \end{matrix} \right.\)
\(\Leftrightarrow \left \{\begin{matrix}96^2 \ – \ 95,5^2 = 4p\\96^2 = 2ph \end{matrix} \right.\)
\(\Leftrightarrow \left \{\begin{matrix}p = \displaystyle \frac{383}{16}\\h \approx 192,5 \end{matrix} \right.\)
Vậy chiều cao của cổng khoảng \(192,5 m\).
\(\)
Bài \(18\). Một người đứng ở giữa một tấm ván gỗ đặt trên một giàn giáo để sơn tường nhà. Biết rằng giàn giáo dài \(16 m\) và độ võng tại tâm của ván gỗ (điểm ở giữa ván gỗ là \(3 cm\)) (Hình \(4\)). Cho biết đường cong của ván gỗ có hình parabol.
\(a)\) Giả sử tâm ván gỗ trùng với đỉnh của parabol, tìm phương trình chính tắc của parabol.
\(b)\) Điểm có độ võng \(1 cm\) cách tâm ván gỗ bao xa?
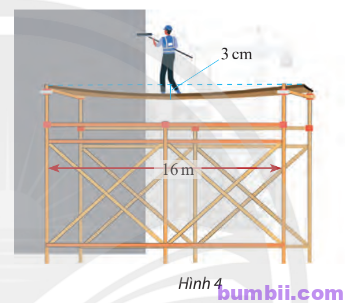
Trả lời:
Vẽ lại parabol và chọn hệ trục toạ độ như hình vẽ:
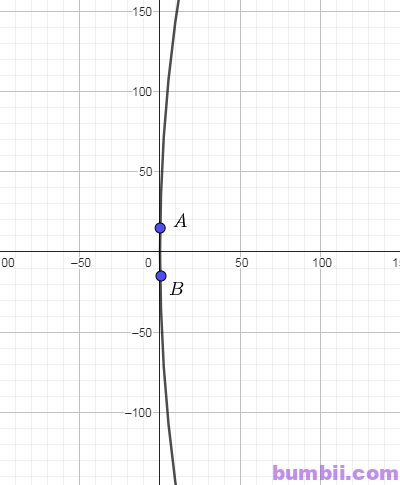
\(a)\) Đổi \(3 cm = 0, 03 m\)
Giả sử phương trình chính tắc của parabol có dạng \(y^2 = 2px\)
Theo bài ra ta có:
\(AB = 2y_A = 16\)
\(\Rightarrow y_A = 8 \Rightarrow A(0,03; 8)\)
Thay toạ độ điểm \(A\) vào phương trình của parabol ta được:
\(8^2 = 2p. 0, 03\)
\(\Rightarrow p = \displaystyle \frac{3200}{3}\)
Vậy phương trình chính tắc của parabol có dạng:
\(y^2 = 2px = \displaystyle \frac{6400}{3}x\)
\(b)\) Điểm có độ võng \(1 cm\) tương ứng với \(x = 0, 03 \ – \ 0,01 = 0,02 m\)
Thay \(x = 0,02\) vào phương trình \(y^2 = \displaystyle \frac{6400}{3}x\) ta được:
\(y^2 = \displaystyle \frac{6400}{3}. 0,02\)
\(\Rightarrow |y| \approx 6,53 m\)
Vậy điểm có độ võng \(1cm\) cách tâm ván gỗ khoảng \(6, 53 m\)
\(\)
Xem bài giải trước: https://bumbii.com/bai-4-ba-duong-conic-trong-mat-phang-toa-do/
Xem bài giải tiếp theo: https://bumbii.com/bai-1-khong-gian-mau-va-bien-co/
Xem các bài giải khác: https://bumbii.com/giai-toan-lop-10-nxb-chan-troi-sang-tao
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech

Hạnh phúc đạt được khi bạn ngừng chờ đợi điều đó xảy ra và thực hiện các bước để biến nó thành hiện thực.