Bài 4. Tích vô hướng của hai vectơ

Bài \(4\). Tích vô hướng của hai vectơ trang \(97\) SGK toán lớp \(10\) tập \(1\) Nhà xuất bản Chân trời sáng tạo. Các em cùng Bumbii giải các bài tập sau.

Bài \(1\). Cho hình vuông \(ABCD\) có cạnh bằng \(a\). Tính các tích vô hướng:
\(\overrightarrow{AB}. \overrightarrow{AD}, \overrightarrow{AB}. \overrightarrow{AC}, \overrightarrow{AC}. \overrightarrow{CB}, \overrightarrow{AC}. \overrightarrow{BD}\).

Trả lời:

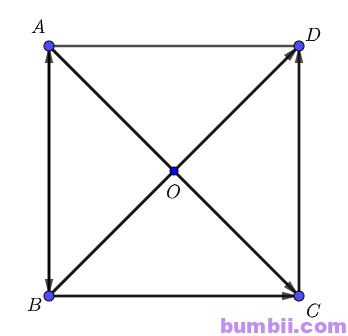
Ta có: Hình vuông \(ABCD\) có hai đường chéo \(AD\) và \(BC\)

\(\Rightarrow AD = BC = \sqrt{AB^2 + BC^2} = \sqrt{a^2 + a^2}\)

\( = a\sqrt{2}\).

\(\overrightarrow{AB}. \overrightarrow{AD} = |\overrightarrow{AB}| . |\overrightarrow{AD}|. \cos\left(\overrightarrow{AB}, \overrightarrow{AD}\right)\)

\(= |\overrightarrow{AB}| . |\overrightarrow{AD}|. \cos90^o = 0\) ( Do \(AB \perp AD\))

\(\overrightarrow{AB}. \overrightarrow{AC} = |\overrightarrow{AB}| . |\overrightarrow{AC}|. \cos\left(\overrightarrow{AB}, \overrightarrow{AC}\right)\)

\(= a. a. \cos45^o = \displaystyle \frac{a^2\sqrt{2}}{2}\)

\(\overrightarrow{AC}. \overrightarrow{CB} = \left(\ – \ \overrightarrow{CA}\right). \overrightarrow{CB} = \ – \ \left(\overrightarrow{CA}.\overrightarrow{CB}\right)\)

\(= \ – \ \left(\overrightarrow{CA}. \overrightarrow{CB}. \cos{\left(\overrightarrow{CA}, \overrightarrow{CB}\right)}\right)\)

\( = \ – \ \left(CA. CB. \cos{\widehat{ACB}}\right)\)

\(= \ – \ \left(a\sqrt{2}. a. \cos45^o\right) = \ – \ a^2\).

Do \(AC \perp BD\) nên \(\overrightarrow{AC}. \overrightarrow{BD} = 0\)

\(\)

Bài \(2\). Cho hình chữ nhật \(ABCD\) có tâm \(O\) và \(AD = a, AB = 2a\). Tính:
\(a)\) \(\overrightarrow{AB}. \overrightarrow{AO}\);
\(b)\) \(\overrightarrow{AB}. \overrightarrow{AD}\).

Trả lời:

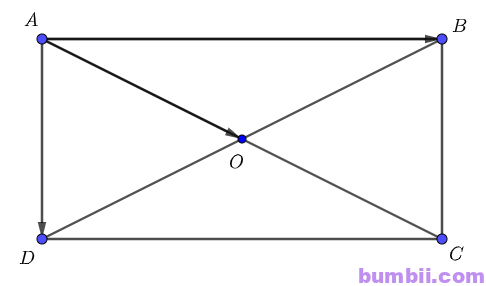
Xét hình chữ nhật \(ABCD\) có hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(O\) là trung điểm của mỗi đường.

\(\Rightarrow AC = BD = \sqrt{AB^2 + BC^2} = \sqrt{a^2 + (2a)^2}\)

\( = a\sqrt{5}\)

\(\Rightarrow AO = \displaystyle \frac{1}{2}. AC = \displaystyle \frac{1}{2}. a\sqrt{5} = \displaystyle \frac{a\sqrt{5}}{2}\)

Ta có: \(\cos{\widehat{BAO}} = \cos{\widehat{BAC}} = \displaystyle \frac{BC}{AB} = \displaystyle \frac{2a}{a\sqrt{5}} = \displaystyle \frac{2}{\sqrt{5}}\)

\(a)\) \(\overrightarrow{AB}. \overrightarrow{AO} = |\overrightarrow{AB}|. |\overrightarrow{AO}|. \cos \left(\overrightarrow{AB}, \overrightarrow{AC}\right)\)

\(= AB. AO. \cos{\widehat{BAO}} = 2a. \displaystyle \frac{a\sqrt{5}}{2}. \displaystyle \frac{2}{\sqrt{5}} = 2a^2\)

\(b)\) \(\overrightarrow{AB}. \overrightarrow{AD} = |\overrightarrow{AB}|. |\overrightarrow{AD}|. \cos \left(\overrightarrow{AB}, \overrightarrow{AD}\right)\)

\(= AB. AD. \cos{\widehat{BAD}} = 2a. a. \cos90^o = 0\)

\(\)

Bài \(3\). Cho ba điểm \(O, A, B\) thẳng hàng và \(OA = a, OB = b\). Tính tích vô hướng \(\overrightarrow{OA}. \overrightarrow{OB}\) trong hai trường hợp:
\(a)\) Điểm \(O\) nằm ngoài đoạn thẳng \(AB\);
\(b)\) Điểm \(O\) nằm trong đoạn thẳng \(AB\).

Trả lời: \(a)\) Điểm \(O\) nằm ngoài đoạn thẳng \(AB\):

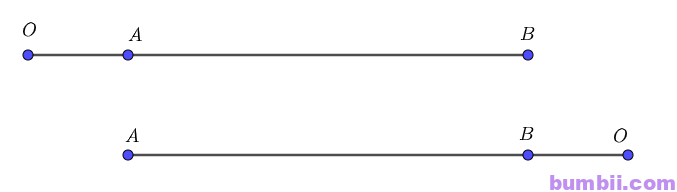
Khi đó ta có: Hai vectơ \(\overrightarrow{OA}, \overrightarrow{OB}\) cùng hướng

\(\Rightarrow \left(\overrightarrow{OA}, \overrightarrow{OB}\right) = 0^o\)

\(\Rightarrow \overrightarrow{OA}. \overrightarrow{OB} = |\overrightarrow{OA}|. |\overrightarrow{OB}|. \cos \left(\overrightarrow{OA}, \overrightarrow{OB}\right)\)

\(= a. b. \cos0^o = ab\)

\(b)\) Điểm \(O\) nằm trong đoạn thẳng \(AB\):

Khi đó ta có: Hai vectơ \(\overrightarrow{OA}, \overrightarrow{OB}\) ngược hướng

\(\Rightarrow \left(\overrightarrow{OA}, \overrightarrow{OB}\right) = 180^o\)

\(\Rightarrow \overrightarrow{OA}. \overrightarrow{OB} = |\overrightarrow{OA}|. |\overrightarrow{OB}|. \cos \left(\overrightarrow{OA}, \overrightarrow{OB}\right)\)

\(= a. b. \cos180^o = \ – \ ab\)

\(\)

Bài \(4\). Cho đoạn thẳng \(AB\) có \(O\) là trung điểm và điểm \(M\) tuỳ ý. Chứng minh rằng:
\(\overrightarrow{MA}. \overrightarrow{MB} = \overrightarrow{MO}^2 \ – \ \overrightarrow{OA}^2\).

Trả lời:

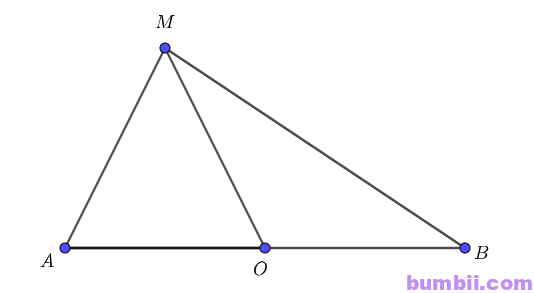
Ta có: \(O\) là trung điểm của đoạn \(AB\) nên:

\(\overrightarrow{OA} + \overrightarrow{OB} = \overrightarrow{0}\)

\(\Leftrightarrow \ – \ \overrightarrow{OA} = \overrightarrow{OB}\)

\(\Rightarrow \overrightarrow{MO}^2 \ – \ \overrightarrow{OA}^2 = \left(\overrightarrow{MO} \ – \ \overrightarrow{OA}\right) \left(\overrightarrow{MO} + \overrightarrow{OA}\right)\)

\(=\left(\overrightarrow{MO} + \overrightarrow{OB}\right) \left(\overrightarrow{MO} + \overrightarrow{OA}\right)\)

\(= \overrightarrow{MB}. \overrightarrow{MA} = \overrightarrow{MA}. \overrightarrow{MB}\)

Vậy \(\overrightarrow{MO}^2 \ – \ \overrightarrow{OA}^2 = \overrightarrow{MA}. \overrightarrow{MB}\) (đpcm)

\(\)

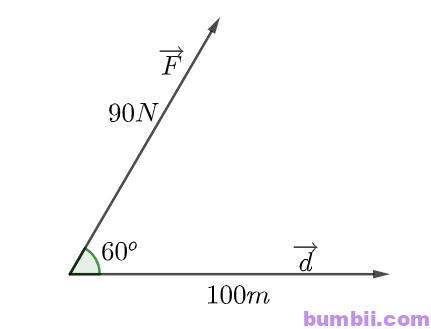
Bài \(5\). Một người dùng một lực \(F\) có độ lớn là \(90N\) làm một vật dịch chuyển một đoạn \(100 m\).
Biết lực \(\overrightarrow{F}\) hợp với hướng dịch chuyển một góc \(60^o\). Tính công sinh bởi lực \(\overrightarrow{F}\).

Trả lời:

Công sinh bởi lực \(\overrightarrow{F}\) được tính bới công thức sau:

\(A = \overrightarrow{F}. \overrightarrow{d} = |\overrightarrow{F}|. |\overrightarrow{d}. \cos{\left(\overrightarrow{F}, \overrightarrow{d}\right)}\)

\(= 90. 100. \cos60^o = 4500 (J) \)

Vậy công sinh bởi lực \(\overrightarrow{F}\) có độ lớn bằng \(4500 J\).

\(\)

Bài \(6\). Cho hai vectơ có độ dài lần lượt là \(3\) và\(4\) và có tích vô hướng là \(\ – \ 6\). Tính góc giữa hai vectơ đó.

Trả lời: Gọi hai vectơ lần lượt là \(\overrightarrow{a}, \overrightarrow{b}\)

Theo bài ra ta có:

\(|\overrightarrow{a}| = 3; |\overrightarrow{b}| = 4; \overrightarrow{a}. \overrightarrow{b} = \ – \ 6\)

Từ đây suy ra:

\(\overrightarrow{a}. \overrightarrow{b} = |\overrightarrow{a}|. |\overrightarrow{b}|. \cos{\left(\overrightarrow{a}, \overrightarrow{b}\right)} = \ – \ 6\)

\(\Leftrightarrow 3. 4. \cos{\left(\overrightarrow{a}, \overrightarrow{b}\right)} = \ – \ 6\)

\(\Leftrightarrow \cos{\left(\overrightarrow{a}, \overrightarrow{b}\right)} = \displaystyle \frac{\ – \ 6}{12} = \displaystyle \frac{\ – \ 1}{2}\)

\(\Leftrightarrow \left(\overrightarrow{a}, \overrightarrow{b}\right) = 120^o\)

Vậy góc giữa hai vectơ cần tìm là \(120^o\).

Bài 4. Tích vô hướng của hai vectơ

Xem bài giải trước: https://bumbii.com/bai-3-tich-cua-mot-so-voi-mot-vecto/
Xem bài giải tiếp theo: https://bumbii.com/bai-tap-cuoi-chuong-v/
Xem các bài giải khác: https://bumbii.com/giai-toan-lop-10-nxb-chan-troi-sang-tao

Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech