Chương 4 – Bài 3: Hai đường thẳng song song trang 80 sách giáo khoa toán lớp 7 tập 1 NXB Chân Trời Sáng Tạo.
\(1.\) Trong Hình \(15\), cho biết a // b. Tìm số đo các góc đỉnh A và B.
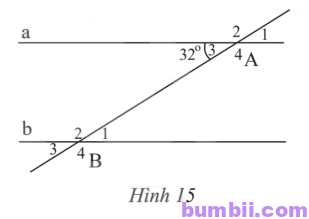
Giải
\(\widehat{A_1}=\widehat{A_3}=32^o\) (hai góc đối đỉnh)
\(\widehat{A_3}+\widehat{A_4}=180^o\) (hai góc kề bù) nên \(\widehat{A_4}=180^o-\widehat{A_3}=180^o-32^o=148^o.\)
\(\widehat{A_2}=\widehat{A_4}=148^o\) (hai góc đối đỉnh)
\(\widehat{B_1}=\widehat{A_3}=32^o\) (hai góc so le trong)
\(\widehat{B_3}=\widehat{B_1}=32^o\) (hai góc đối đỉnh)
\(\widehat{B_4}+\widehat{B_3}=180^o\) (hai góc kề bù) nên \(\widehat{B_4}=180^o-\widehat{B_3}=180^o-32^o=148^o.\)
\(\widehat{B_2}=\widehat{B_4}=148^o\) (hai góc đối đỉnh)
\(\)
\(2.\) Vẽ một đường thẳng cắt hai đường thẳng sao cho trong các góc tạo thành có một cặp góc so le trong bằng nhau. Đặt tên cho các góc đó.
a) Vì sao cặp góc so le trong còn lại cũng bằng nhau?
b) Vì sao các cặp góc đồng vị cũng bằng nhau?
Giải
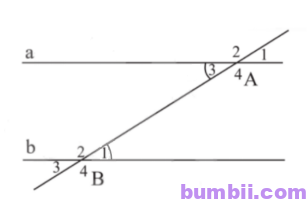
a) \(\widehat{A_3}=\widehat{B_1}\) suy ra a//b (có hai góc ở vị trí so le trong bằng nhau)
Do a//b nên cặp góc so le trong còn lại bằng nhau: \(\widehat{A_4}=\widehat{B_2}.\)
b) Do a//b nên các cặp góc đồng vị cũng bằng nhau:
\(\widehat{A_1}=\widehat{B_1};\ \widehat{A_1}=\widehat{B_2}; \widehat{A_3}=\widehat{B_3};\ \widehat{A_4}=\widehat{B_4}.\)
\(\)
\(3.\) Hãy nói các cách để kiểm tra hai đường thẳng song song mà em biết.
Giải
Để kiểm tra hai đường thẳng song song ta có các cách sau:
-Kiểm tra số đo của một cặp góc so le trong.
-Kiểm tra số đo của một cặp góc đồng vị.
-Kiểm tra tính hai đường thẳng cùng vuông góc với một đường thẳng thứ ba.
-Kiểm tra tính cùng song song với một đường thẳng thứ ba.
\(\)
\(4.\) Cho Hình \(16\), biết a // b.
a) Chỉ ra góc ở vị trí so le trong, đồng vị với góc \(\widehat{B_2}.\)
b) Tính số đo các góc \(\widehat{A_4},\ \widehat{A_2},\ \widehat{B_3}.\)
c) Tính số đo các góc \(\widehat{B_1},\ \widehat{A_1}.\)
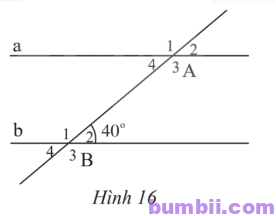
Giải
Do a//b nên ta có:
a) \(\widehat{A_4}\) ở vị trí so le trong với \(\widehat{B_2}\).
\(\widehat{A_2}\) ở vị trí đồng vị với \(\widehat{B_2}\).
b) \(\widehat{A_4}=\widehat{B_2}=40^o\) (hai góc so le trong)
\(\widehat{A_2}=\widehat{B_2}=40^o\) (hai góc đồng vị)
\(\widehat{B_2}+\widehat{B_3}=180^o\) (hai góc kề bù) nên \(\widehat{B_3}=180^o-\widehat{B_2}=180^o-40^o=140^o.\)
c) \(\widehat{B_1}=\widehat{B_3}=140^o\) (hai góc đối đỉnh)
\(\widehat{A_1}=\widehat{B_1}=140^o\) (hai góc đồng vị)
\(\)
\(5.\) Cho Hình 17, biết a // b. Tính số đo của các góc \(\widehat{B_1}\) và \(\widehat{D_1}\).
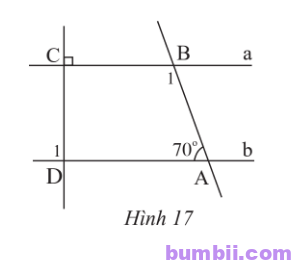
Giải
Vì a//b nên ta có:
\(\widehat{ABa}=\widehat{BAD}=70^o\) (hai góc so le trong)
\(\widehat{CBA}+\widehat{ABa}=180^o\) (hai góc kề bù) nên \(\widehat{CBA}=180^o-\widehat{ABa}=180^o-70^o=110^o\)
\(\widehat{CDA}=\widehat{C}=90^o\) (hai góc đồng vị)
\(\widehat{D_1}+\widehat{CDA}=180^o\) (hai góc kề bù) nên \(\widehat{D_1}=180^o-\widehat{CDA}=180^o-90^o=90^o\)
\(\)
\(6.\) Cho Hình \(18\), biết \(\widehat{B_1} =40^o,\ \widehat{C_2} =40^o\).
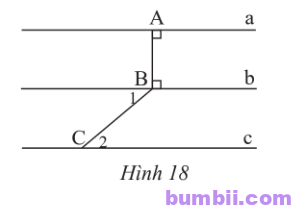
a) Đường thẳng a có song song với đường thẳng b không? Vì sao?
b) Đường thẳng b có song song với đường thẳng c không? Vì sao?
c) Đường thẳng a có song song với đường thẳng c không? Vì sao?
Giải
a) Đường thẳng AB vuông góc với a; đường thẳng AB vuông góc với b nên a // b (hai đường thẳng cùng vuông góc với đường thẳng thứ ba)
b) Do \(\widehat{B_1} = \widehat{C_2} = 40^o\), mà hai góc này ở vị trí so le trong nên b // c.
c) Do a // b và b // c suy ra a // c.
\(\)
\(7.\) Quan sát Hình \(19\) và cho biết:
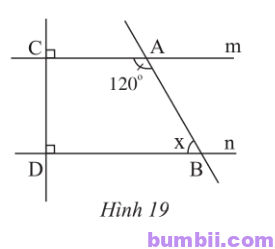
a) Vì sao m // n?
b) Số đo x của góc \(\widehat{ABD}\) là bao nhiêu?
Giải
a) vì m và n cùng vuông góc với CD nên m // n.
b) m//n => \(\widehat{CAB}=\widehat{ABn}=120^o\) (hai góc so le trong)
\(\widehat{ABD}+\widehat{ABn}=180^o\) (hai góc kề bù) nên \(\widehat{ABD}=180^o-\widehat{ABn}=180^o-120^o=60^o\)
Vậy \(x=60^o.\)
\(\)
Xem thêm các bài giải khác tại: Giải bài tập SGK Toán Lớp 7 – NXB Chân Trời Sáng Tạo.
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech
