Chương 4 – Bài 3: Hai đường thẳng song song trang 110 sách bài tập toán lớp 7 tập 1 NXB Cánh Diều. Các em cùng Bumbii giải các bài tập sau.
16. Quan sát Hình 28, biết a // b, \(\widehat{M_3}=50^o.\)
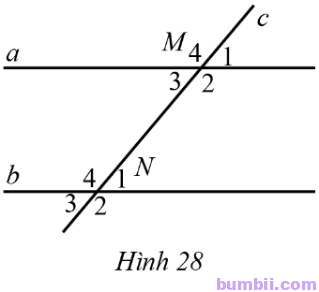
a) Nêu những cặp góc so le trong, những cặp góc đồng vị.
b) Tìm số đo mỗi góc còn lại của đỉnh M và N.
Giải
a) Những cặp góc so le trong là: \(\widehat{M_2}\) và \(\widehat{N_4};\) \(\widehat{M_3}\) và \(\widehat{N_1}.\)
Những cặp góc đồng vị là: \(\widehat{M_1}\) và \(\widehat{N_1},\) \(\widehat{M_2}\) và \(\widehat{N_2},\) \(\widehat{M_3}\) và \(\widehat{N_3};\) \(\widehat{M_4}\) và \(\widehat{N_4}.\)
b) Ta có \(\widehat{M_2}+\widehat{M_3}=180^o\) (hai góc kề bù) nên
\(\widehat{M_2}=180^o-\widehat{M_3}=180^o-50^o=130^o.\)
Ta có \(\widehat{M_1}=\widehat{M_3}=50^o;\) \(\widehat{M_2}=\widehat{M_4}=130^o\) (các cặp góc đối đỉnh).
Vì a // b nên
\(\widehat{N_1}=\widehat{M_3}=50^o\) (so le trong);
\(\widehat{N_2}=\widehat{M_2}=130^o\) (đồng vị);
\(\widehat{N_3}=\widehat{M_3}=50^o\) (đồng vị);
\(\widehat{N_4}=\widehat{M_2}=130^o\) (so le trong).
\(\)
17. Quan sát Hình 29, biết a // b, \(3\widehat{A_1}=2\widehat{A_2}.\)
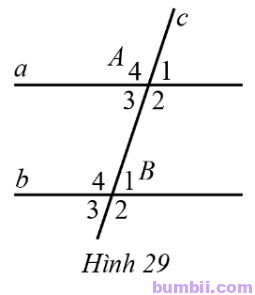
Giải
Ta có \(3\widehat{A_1}=2\widehat{A_2}\) hay \(\widehat{A_2}=\displaystyle\frac{3}{2}\widehat{A_1}\) và \(\widehat{A_1}+\widehat{A_2}=180^o\) (hai góc kề bù)
Nên \(\widehat{A_1}+\displaystyle\frac{3}{2}\widehat{A_1}=\displaystyle\frac{5}{2}\widehat{A_1}=180^o\)
Suy ra \(\widehat{A_1}=180^o:\displaystyle\frac{5}{3}=72^o.\)
Do đó \(\widehat{A_2}=\displaystyle\frac{2}{3}\widehat{A_1}=\displaystyle\frac{3}{2}.72^o=108^o.\)
Suy ra \(\widehat{A_1}=\widehat{A_3}=72^o;\) \(\widehat{A_2}=\widehat{A_4}=108^o\) (các cặp góc đối đỉnh).
Vì a // b nên ta có:
\(\widehat{B_1}=\widehat{A_3}=72^o\) (so le trong).
\(\widehat{B_2}=\widehat{A_2}=108^o\) (đồng vị).
\(\widehat{B_3}=\widehat{A_3}=72^o\) (đồng vị).
\(\widehat{B_4}=\widehat{A_2}=108^o\) (so le trong).
Vậy \(\widehat{A_1}=\widehat{A_3}=\widehat{B_1}=\widehat{B_3}=72^o,\) \(\widehat{A_2}=\widehat{A_4}=\widehat{B_2}=\widehat{B_4}=108^o.\)
\(\)
18. Tìm số đo mỗi góc \(B_1,\ B_2,\) \(B_3,\ B_4\) trong Hình 30, biết m // n.
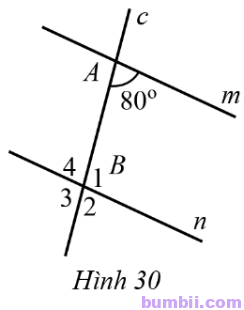
Giải
Do m // n nên \(\widehat{B_2}=80^o\) (đồng vị với góc \(80^o\)); \(\widehat{B_4}=\widehat{B_2}=80^o\) (đối đỉnh).
Ta có \(\widehat{B_2}+\widehat{B_1}=180^o\) (hai góc kề bù)
\(\widehat{B_1}=180^o-\widehat{B_2}=180^o-80^o=100^o.\)
Do đó \(\widehat{B_3}=\widehat{B_1}=100^o\) (đối đỉnh).
Vậy \(\widehat{B_1}=\widehat{B_3}=100^o,\) \(\widehat{B_2}=\widehat{B_4}=80^o.\)
\(\)
19. Quan sát Hình 31, biết \(\widehat{P_3}=\widehat{Q_1}=75^o,\) \(\widehat{M_3}=100^o.\) Tìm số đo mỗi góc còn lại của đỉnh M và N.
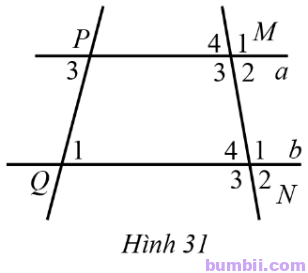
Giải
Ta có: \(\widehat{M_1}=\widehat{M_3}=100^o\) (đối đỉnh).
\(\widehat{M_1}+\widehat{M_2}=180^o\) (hai góc kề bù)
\(\widehat{M_2}=180^o-\widehat{M_1}=180^o-100^o=80^o.\)
Do đó \(\widehat{M_4}=\widehat{M_2}=80^o\) (đối đỉnh).
Ta có \(\widehat{P_3}=\widehat{Q_1}=75^o\) mà hai góc này ở vị trí so le trong nên PM // QN.
Do đó \(\widehat{N_1}=\widehat{M_3}=100^o\) (so le trong).
\(\widehat{N_2}=\widehat{M_2}=80^o\) (đồng vị).
\(\widehat{N_3}=\widehat{M_3}=100^o\) (đồng vị).
\(\widehat{N_4}=\widehat{M_2}=80^o\) (so le trong).
Vậy \(\widehat{M_3}=\widehat{N_1}=\widehat{N_3}=100^o;\) \(\widehat{M_2}=\widehat{M_4}=\widehat{N_2}=\widehat{N_4}=80^o.\)
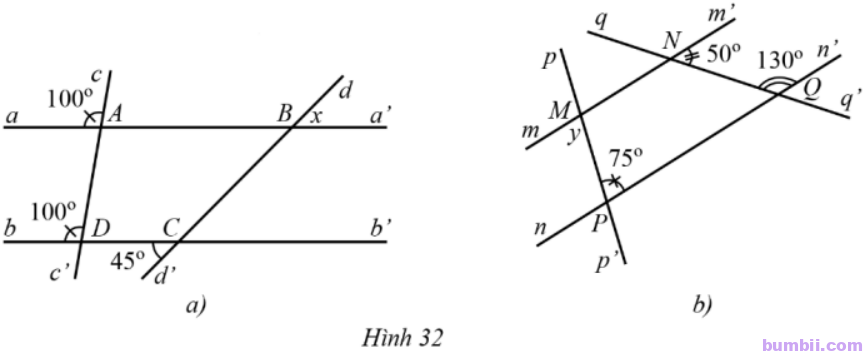
20. Tìm số đo \(x,\ y\) trong Hình 32.
Giải
a) Ta có \(\widehat{aAc}=\widehat{bDc}\) (cùng bằng \(100^o\)).
Mà hai góc này ở vị trí đồng vị nên đó aa’ // bb’.
Suy ra \(\widehat{dBa’}=\widehat{bCd’}=45^o\) (hai góc so le ngoài).
Vậy \(x = 45^o.\)
b) Ta có \(\widehat{qQn}+\widehat{qQn’}=180^o\) (hai góc kề bù)
\(\widehat{qQn}=180^o-\widehat{qQn’}=180^o-130^o=50^o.\)
Do đó \(\widehat{m’Nq’}=\widehat{qQn}\) (cùng bằng \(50^o\)).
Mà hai góc này ở vị trí so le trong nên mm’ // nn’.
Suy ra \(\widehat{mMp’}=\widehat{pPn’}=75^o\) (so le trong).
Vậy \(y = 75^o.\)
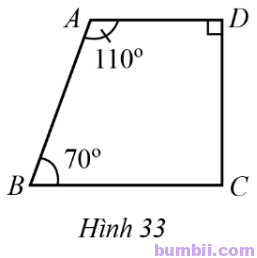
21. Tìm số đo góc BCD trong Hình 33.
Giải
Ta có \(\widehat{A} +\widehat{B} =110^o+70^o=180^o\) hai góc này bù nhau mà chúng ở vị trí trong cùng phía nên AD // BC.
Suy ra \(\widehat{BCD}+\widehat{D}=180^o\) (hai góc trong cùng phía)
\(\widehat{BCD}=180^o-\widehat{D}=180^o-90^o=90^o.\)
Vậy \(\widehat{BCD}=90^o.\)
\(\)
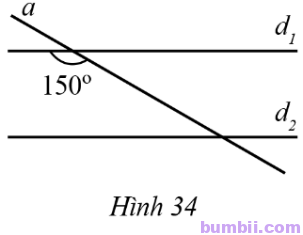
22. Quan sát Hình 34, biết \(d_1\) // \(d_2\) và góc tù tạo bởi đường thẳng a và đường thẳng \(d_1\) bằng \(150^o.\) Tính góc nhọn tạo bởi đường thẳng a và đường thẳng \(d_2.\)
Giải
Ta có \(d_1\) // \(d_2\) nên góc tạo bởi đường thẳng \(a\) và đường thẳng \(d_1\) với góc nhọn tạo bởi đường thẳng \(a\) và đường thẳng \(d_2\) là hai góc trong cùng phía bù nhau.
Suy ra góc nhọn tạo bởi đường thẳng \(a\) và đường thẳng \(d_2\) bằng \(180^o-150^o=30^o. \)
\(\)
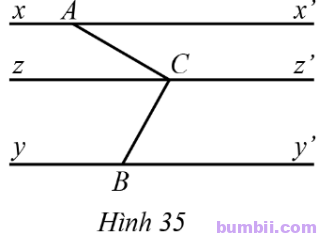
23. Quan sát Hình 35, biết xx’ // yy’ // zz’. Chứng tỏ rằng \(\widehat{ACB}=\widehat{CAx’}+\widehat{CBy’}.\)
Giải
Do xx’ // zz’ nên \(\widehat{CAx’}=\widehat{ACz}\) (so le trong).
Do yy’ // zz’ nên \(\widehat{zCB}=\widehat{CBy’}\) (so le trong).
Do \(\widehat{ACz}\) và \(\widehat{zCB}\) là hai góc kề nhau nên
\(\widehat{ACB}=\widehat{ACz}+\widehat{zCB}=\widehat{CAx’}+\widehat{zCB}.\)
\(\)
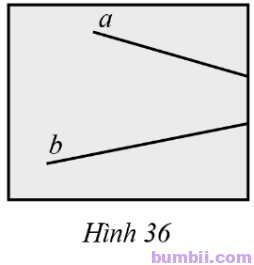
24*. Bạn Khôi vẽ hai đường thẳng a và b cắt nhau tại một điểm ở ngoài phạm vi tờ giấy (Hình 36). Em hãy giúp bạn Khôi nêu cách đo góc nhọn tạo bởi hai đường thẳng a và b đã vẽ.
Giải
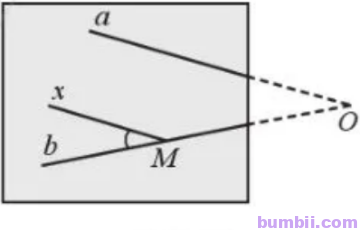
Lấy M ∈ b. Kẻ Mx // a với \(\widehat{bMx} <90^o.\) Khi đó góc nhọn tạo bởi hai đường thẳng a và b bằng góc bMx (hai góc đòng vị). Do đó ta đo góc bMx sẽ suy ra góc nhọn tạo bởi hai đường thẳng a và b.
\(\)
Xem bài giải trước: Bài 2: Tia phân giác của một góc
Xem bài giải tiếp theo: Bài 4: Định lý
Xem thêm các bài giải khác tại: Giải Bài tập Toán Lớp 7 Cánh Diều
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech
