Bài \(3\). Các công thức lượng giác trang \(20\) Sách giáo khoa Toán lớp \(11\) tập \(1\) Chân trời sáng tạo. Các em cùng Bumbii giải các bài tập sau:
Bài \(1\). Không dùng máy tính cầm tay, tính các giá trị lượng giác của các góc:
\(a)\) \(\displaystyle \frac{5\pi}{12}\);
\(b)\) \(\ – \ 555^o\).
Trả lời:
\(a)\) Ta có:
\(+)\) \(\sin{\displaystyle \frac{5\pi}{12}} = \sin{\left(\displaystyle \frac{3\pi}{12} + \displaystyle \frac{2\pi}{12}\right)} = \sin{\left(\displaystyle \frac{\pi}{4} + \displaystyle \frac{\pi}{6}\right)}\)
\(= \sin{\displaystyle \frac{\pi}{4}}. \cos{\displaystyle \frac{\pi}{6}} + \cos{\displaystyle \frac{\pi}{4}}. \sin{\displaystyle \frac{\pi}{6}}\)
\(= \displaystyle \frac{\sqrt{2}}{2}. \displaystyle \frac{\sqrt{3}}{2} + \displaystyle \frac{\sqrt{2}}{2}. \displaystyle \frac{1}{2} = \displaystyle \frac{\sqrt{6}}{4} + \displaystyle \frac{\sqrt{2}}{4} = \displaystyle \frac{\sqrt{6} + \sqrt{2}}{4}\)
\(+)\) \(\cos{\displaystyle \frac{5\pi}{12}} = \cos{\left(\displaystyle \frac{\pi}{4} + \displaystyle \frac{\pi}{6}\right)}\)
\(= \cos{\displaystyle \frac{\pi}{4}}. \cos{\displaystyle \frac{\pi}{6}} \ – \ \sin{\displaystyle \frac{\pi}{4}}. \sin{\displaystyle \frac{\pi}{6}}\)
\( = \displaystyle \frac{\sqrt{2}}{2}. \displaystyle \frac{\sqrt{3}}{2} \ – \ \displaystyle \frac{\sqrt{2}}{2}. \displaystyle \frac{1}{2} = \displaystyle \frac{\sqrt{6}}{4} \ – \ \displaystyle \frac{\sqrt{2}}{4} = \displaystyle \frac{\sqrt{6} \ – \ \sqrt{2}}{4}\)
\(+)\) \(\tan{\displaystyle \frac{5\pi}{12}} = \displaystyle \frac{\sin{\displaystyle \frac{5\pi}{12}}}{\cos{\displaystyle \frac{5\pi}{12}}} = \displaystyle \frac{\sqrt{6} \ – \ \sqrt{2}}{\sqrt{6} + \sqrt{2}} = 2 \ – \ \sqrt{3}\)
\(+)\) \(\cot{\displaystyle \frac{5\pi}{12}} = \displaystyle \frac{1}{\tan{\displaystyle \frac{5\pi}{12}}} = \displaystyle \frac{1}{2 \ – \ \sqrt{3}} = 2 + \sqrt{3}\)
\(b)\) Ta có: \(\ – \ 555^o = \ – \ \displaystyle \frac{555\pi}{180}\)
\(= \ – \ \displaystyle \frac{37\pi}{12} = \ – \ \left(3\pi + \displaystyle \frac{\pi}{12}\right)\)
\(+)\) \(\sin{(\ – \ 555^o)} = \sin{\ – \ \left(3\pi + \displaystyle \frac{\pi}{12}\right)} = \sin{\displaystyle \frac{\pi}{12}}\)
\(= \sin{\left(\displaystyle \frac{\pi}{3} \ – \ \displaystyle \frac{\pi}{4}\right)} = \sin{\displaystyle \frac{\pi}{3}}. \cos{\displaystyle \frac{\pi}{4}} \ – \ \cos{\displaystyle \frac{\pi}{3}}. \sin{\displaystyle \frac{\pi}{4}}\)
\( = \displaystyle \frac{\sqrt{3}}{2}. \displaystyle \frac{\sqrt{2}}{2} \ – \ \displaystyle \frac{1}{2}. \displaystyle \frac{\sqrt{2}}{2} = \displaystyle \frac{\sqrt{6} \ – \ \sqrt{2}}{4}\)
\(+)\) \(\cos{(\ – \ 555^o)} = \cos{\ – \ \left(3\pi + \displaystyle \frac{\pi}{12}\right)} = \ – \ \cos{\displaystyle \frac{\pi}{12}}\)
\( = \ – \ \cos{\left(\displaystyle \frac{\pi}{3} \ – \ \displaystyle \frac{\pi}{4}\right)} = \ – \ \left(\cos{\displaystyle \frac{\pi}{3}}\cos{\displaystyle \frac{\pi}{4}} + \sin{\displaystyle \frac{\pi}{3}}\sin{\displaystyle \frac{\pi}{4}}\right)\)
\(= \ – \ \left(\displaystyle \frac{1}{2}. \displaystyle \frac{\sqrt{2}}{2} + \displaystyle \frac{\sqrt{3}}{2}. \displaystyle \frac{\sqrt{2}}{2} \right) = \ – \ \displaystyle \frac{\sqrt{2} + \sqrt{6}}{4}\)
\(+)\) \(\tan{(\ – \ 555^o)} = \displaystyle \frac{\sin{(\ – \ 555^o)}}{\cos{(\ – \ 555^o)}} = \displaystyle \frac{\displaystyle \frac{\sqrt{6} \ – \ \sqrt{2}}{4}}{\ – \ \displaystyle \frac{\sqrt{6} + \sqrt{2}}{4}}\)
\(= \ – \ 2 + \sqrt{3}\)
\(+)\) \(\cot{(\ – \ 555^o)} = \displaystyle \frac{1}{\tan{(\ – \ 555^o)}} = \displaystyle \frac{1}{\ – \ 2 + \sqrt{3}}\)
\( = \ – \ 2 \ – \ \sqrt{3}\)
\(\)
Bài \(2\). Tính \(\sin{\left(\alpha + \displaystyle \frac{\pi}{6}\right)}; \cos{\left(\displaystyle \frac{\pi}{4} \ – \ \alpha\right)}\) biết \(\sin{\alpha} = \ – \ \displaystyle \frac{5}{13} \text{ và } \displaystyle \frac{\pi}{2} < \alpha < \displaystyle \frac{3\pi}{2}\).
Trả lời:
Với \(\displaystyle \frac{\pi}{2} < \alpha < \displaystyle \frac{3\pi}{2}\) thì \(\cos{\alpha} < 0\)
\(\Rightarrow \cos{\alpha} = \ – \ \sqrt{1 \ – \ \sin^2{\alpha}} = \ – \ \sqrt{1 \ – \ \left(\ – \ \displaystyle \frac{5}{13}\right)^2}\)
\(= \ – \ \sqrt{1 \ – \ \displaystyle \frac{25}{169}} = \ – \ \sqrt{\displaystyle \frac{144}{169}} = \ – \ \displaystyle \frac{12}{13}\) (vì \(\cos{\alpha} < 0\))
Suy ra: \(\sin{\left(\alpha + \displaystyle \frac{\pi}{6}\right)} = \sin{\alpha}. \cos{\displaystyle \frac{\pi}{6}} + \cos{\alpha}. \sin{\displaystyle \frac{\pi}{6}}\)
\(= \left(\ – \ \displaystyle \frac{5}{13}\right). \displaystyle \frac{\sqrt{3}}{2} + \left(\ – \ \displaystyle \frac{12}{13}\right). \displaystyle \frac{1}{2} = \ – \ \displaystyle \frac{12 + 5\sqrt{3}}{26}\)
\(\cos{\left(\displaystyle \frac{\pi}{4} \ – \ \alpha\right)} = \cos{\displaystyle \frac{\pi}{4}}. \cos{\alpha} + \sin{\displaystyle \frac{\pi}{4}}. \sin{\alpha}\)
\( = \displaystyle \frac{\sqrt{2}}{2}. \left(\ – \ \displaystyle \frac{12}{13}\right) + \displaystyle \frac{\sqrt{2}}{2}. \left(\ – \ \displaystyle \frac{5}{13}\right) = \ – \ \displaystyle \frac{17\sqrt{2}}{26}\)
\(\)
Bài \(3\). Tính các giá trị lượng giác của góc \(2\alpha\), biết:
\(a)\) \(\sin{\alpha} = \displaystyle \frac{\sqrt{3}}{3} \text{ và } 0 < \alpha < \displaystyle \frac{\pi}{2}\);
\(b)\) \(\sin{\displaystyle \frac{\alpha}{2}} = \displaystyle \frac{3}{4} \text{ và } \pi < \alpha < 2\pi\).
Trả lời:
\(a)\) Với \(0 < \alpha < \displaystyle \frac{\pi}{2}\) thì \(\cos{\alpha} > 0\)
\(\Rightarrow \cos{\alpha} = \sqrt{1 \ – \ \sin^2{\alpha}} = \sqrt{1 \ – \ \left(\displaystyle \frac{\sqrt{3}}{3}\right)^2} = \displaystyle \frac{\sqrt{6}}{3}\) (vì \(\cos{\alpha} > 0\))
Khi đó ta có:
\(\sin{2\alpha} = 2\sin{\alpha}\cos{\alpha} = 2. \displaystyle \frac{\sqrt{3}}{3}. \displaystyle \frac{\sqrt{6}}{3} = \displaystyle \frac{2\sqrt{2}}{3}\)
\(\Rightarrow \cos{2\alpha} = \sqrt{1 \ – \ \sin^2{2\alpha}} = \sqrt{1 \ – \ \left(\displaystyle \frac{2\sqrt{2}}{3}\right)^2} = \displaystyle \frac{1}{3}\)
\(\Rightarrow \tan{2\alpha} = \displaystyle \frac{\sin{2\alpha}}{\cos{2\alpha}} = \displaystyle \frac{\displaystyle \frac{2\sqrt{2}}{3}}{\displaystyle \frac{1}{3}} = 2\sqrt{2}\)
\(\Rightarrow \cot{2\alpha} = \displaystyle \frac{1}{\tan{2\alpha}} = \displaystyle \frac{1}{2\sqrt{2}} = \displaystyle \frac{\sqrt{2}}{4}\)
\(b)\) Với \(\pi < \alpha < 2\pi\) thì \(\displaystyle \frac{\pi}{2} < \displaystyle \frac{\alpha}{2} < \pi\) nên \(\cos{\displaystyle \frac{\alpha}{2}} < 0\).
\(\Rightarrow \cos{\displaystyle \frac{\alpha}{2}} = \ – \ \sqrt{1 \ – \ \sin^2{\displaystyle \frac{\alpha}{2}}} = \ – \ \sqrt{1 \ – \ \left(\displaystyle \frac{3}{4}\right)^2}\)
\(= \ – \ \displaystyle \frac{\sqrt{7}}{4}\) (vì \(\cos{\displaystyle \frac{\alpha}{2}} < 0\))
Khi đó ta có:
\(\sin{\alpha} = 2\sin{\displaystyle \frac{\alpha}{2}}. \cos{\displaystyle \frac{\alpha}{2}} = 2. \displaystyle \frac{3}{4}. \left(\ – \ \displaystyle \frac{\sqrt{7}}{4}\right)\)
\(= \ – \ \displaystyle \frac{3\sqrt{7}}{8}\)
\(\cos{\alpha} = 2\cos^2{\displaystyle \frac{\alpha}{2}} \ – \ 1 = 2. \displaystyle \frac{7}{16} \ – \ 1 = \ – \ \displaystyle \frac{1}{8}\)
\(\Rightarrow \sin{2\alpha} = 2 \sin{\alpha}. \cos{\alpha} = 2. \left(\ – \ \displaystyle \frac{3\sqrt{7}}{8}\right). \left(\ – \ \displaystyle \frac{1}{8}\right)\)
\(= \displaystyle \frac{3\sqrt{7}}{32}\)
\(\cos{2\alpha} = 2 \cos^2{\alpha} \ – \ 1 = 2. \left(\ – \ \displaystyle \frac{1}{8}\right)^2 \ – \ 1 = \ – \ \displaystyle \frac{31}{32}\)
\(\tan{2\alpha} = \displaystyle \frac{\sin{2\alpha}}{\cos{2\alpha}} = \displaystyle \frac{\displaystyle \frac{3\sqrt{7}}{32}}{\displaystyle \frac{\ – \ 31}{32}} = \ – \ \displaystyle \frac{3\sqrt{7}}{31}\)
\(\Rightarrow \cot{2\alpha} = \displaystyle \frac{1}{\tan{2\alpha}} = \ – \ \displaystyle \frac{31}{3\sqrt{7}}\)
\(\)
Bài \(4\). Rút gọn các biểu thức sau:
\(a)\) \(\sqrt{2}\sin{\left(\alpha + \displaystyle \frac{\pi}{4}\right)} \ – \ \cos{\alpha}\);
\(b)\) \((\cos{\alpha} + \sin{\alpha})^2 \ – \ \sin{2\alpha}\).
Trả lời:
\(a)\) Ta có: \(\sqrt{2}\sin{\left(\alpha + \displaystyle \frac{\pi}{4}\right)} \ – \ \cos{\alpha}\)
\(= \sqrt{2}. \left(\sin{\alpha}\cos{\displaystyle \frac{\pi}{4}} + \cos{\alpha}\sin{\displaystyle \frac{\pi}{4}}\right) \ – \ \cos{\alpha}\)
\(= \sqrt{2}. \left(\displaystyle \frac{\sqrt{2}}{2}.\sin{\alpha} + \displaystyle \frac{\sqrt{2}}{2}\cos{\alpha}\right) \ – \ \cos{\alpha}\)
\(= \sin{\alpha} + \cos{\alpha} \ – \ \cos{\alpha} = \cos{\alpha}\)
\(b)\) \((\cos{\alpha} + \sin{\alpha})^2 \ – \ \sin{2\alpha}\)
\(= \cos^2{\alpha} + \sin^2{\alpha} + 2\sin{\alpha}\cos{\alpha} \ – \ \sin{2\alpha}\)
\(= 1 + \sin{2\alpha} \ – \ \sin{2\alpha}\)
\(= 1 \)
\(\)
Bài \(5\). Tính các giá trị lượng giác của góc \(\alpha\), biết:
\(a)\) \(\cos{2\alpha} = \displaystyle \frac{2}{5} \text{ và } \ – \ \displaystyle \frac{\pi}{2} < \alpha < 0\);
\(b)\) \(\sin{2\alpha} = \ – \ \displaystyle \frac{4}{9} \text{ và } \displaystyle \frac{\pi}{2} < \alpha < \displaystyle \frac{3\pi}{4}\).
Trả lời:
\(a)\) Với \(\ – \ \displaystyle \frac{\pi}{2} < \alpha < 0\) thì \(\sin{\alpha} < 0 \text{ và } \cos{\alpha} > 0\)
Ta có:
\(\cos{2\alpha} = 2\cos^2{\alpha} \ – \ 1 = \displaystyle \frac{2}{5}\)
\(\Rightarrow \cos^2{\alpha} = \displaystyle \frac{1 + \displaystyle \frac{2}{5}}{2} = \displaystyle \frac{7}{10}\)
\(\Rightarrow \cos{\alpha} = \displaystyle \frac{\sqrt{70}}{10}\)
Lại có: \(\sin^2{\alpha} + \cos^2{\alpha} = 1\)
\(\Rightarrow \sin^2{\alpha} = \displaystyle \frac{30}{100}\)
\(\Rightarrow \sin{\alpha} = \ – \ \displaystyle \frac{\sqrt{30}}{10}\) (vì \(\sin{\alpha} < 0\))
Khi đó ta có:
\(\tan{\alpha} = \displaystyle \frac{\sin{\alpha}}{\cos{\alpha}} = \displaystyle \frac{\ – \ \displaystyle \frac{\sqrt{30}}{10}}{\displaystyle \frac{\sqrt{70}}{10}} = \ – \ \displaystyle \frac{\sqrt{3}}{\sqrt{7}}\)
\(\Rightarrow \cot{\alpha} = \displaystyle \frac{1}{\tan{\alpha}} = \ – \ \displaystyle \frac{\sqrt{7}}{\sqrt{3}}\)
\(b)\) Với \(\displaystyle \frac{\pi}{2} < \alpha < \displaystyle \frac{3\pi}{4}\) thì \(\pi < 2\alpha < \displaystyle \frac{3\pi}{2}\) ta có \(\cos{2\alpha} < 0, \sin{\alpha} > 0, \cos{\alpha} < 0\)
\(\Rightarrow \cos{2\alpha} = \ – \ \sqrt{1 \ – \ \sin^2{2\alpha}} = \ – \ \sqrt{1 \ – \ \left(\ – \ \displaystyle \frac{4}{9}\right)^2}\)
\(= \ – \ \displaystyle \frac{\sqrt{65}}{9}\)
Ta có: \(\cos{2\alpha} = 2\cos^2{\alpha} \ – \ 1 = \ – \ \displaystyle \frac{\sqrt{65}}{9}\)
\(\Rightarrow \cos^2{\alpha} = \displaystyle \frac{9 \ – \ \sqrt{65}}{18}\)
\(\Rightarrow \cos{\alpha} = \ – \ \sqrt{\displaystyle \frac{9 \ – \ \sqrt{65}}{18}}\) (vì \(\cos{\alpha} < 0\))
Lại có: \(\sin^2{\alpha} + \cos^2{\alpha} = 1\)
\(\Rightarrow \sin{\alpha} = \sqrt{1 \ – \ \cos^2{\alpha}} = \sqrt{1 \ – \ \displaystyle \frac{9 \ – \ \sqrt{65}}{18}}\)
\( = \sqrt{\displaystyle \frac{9 + \sqrt{65}}{18}}\) (vì \(\sin{\alpha} > 0\))
\(\Rightarrow \tan{\alpha} = \displaystyle \frac{\sin{\alpha}}{\cos{\alpha}} = \ – \ \sqrt{\displaystyle \frac{9 + \sqrt{65}}{9 \ – \ \sqrt{65}}}\)
\(\cot{\alpha} = \ – \ \sqrt{\displaystyle \frac{9 \ – \ \sqrt{65}}{9 + \sqrt{65}}}\)
\(\)
Bài \(6\). Chứng minh rằng trong tam giác \(ABC\), ta có \(\sin{A} = \sin{B}\cos{C} + \sin{C}\cos{B}\).
Trả lời:
Xét tam giác \(ABC\) có:
\(\widehat{A} + \widehat{B} + \widehat{C} = 180^o\)
\(\Rightarrow \widehat{A} = 180^o \ – \ (\widehat{B} + \widehat{C})\)
Suy ra: \(\sin{A} = \sin\left(180^o \ – \ (B + C)\right) = \sin{(B+ C)}\)
\(= \sin{B}\cos{C} + \sin{C}\cos{B}\) (đpcm)
\(\)
Bài \(7\). Trong Hình \(3\), tam giác \(ABC\) vuông tại \(B\) và có hai cạnh góc vuông là \(AB = 4 \text{ và } BC = 3\). Vẽ điểm \(D\) nằm trên tia đối của tia \(CB\) thoả mãn \(\widehat{CAD} = 30^o\). Tính \(\tan{\widehat{BAD}}\), từ đó tính độ dài cạnh \(CD\).
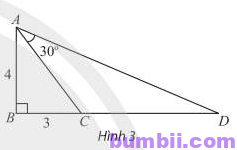
Trả lời:
Xét tam giác \(ABC\) vuông tại \(B\) ta có:
\(\tan{\widehat{BAC}} = \displaystyle \frac{BC}{AB} = \displaystyle \frac{3}{4}\)
Lại có: \(\widehat{BAD} = \widehat{BAC} + \widehat{CAD}\)
\(\Rightarrow \tan{\widehat{BAD}} = \tan{(\widehat{BAC} + \widehat{CAD})} = \tan{(\widehat{BAC} + 30^o)}\)
\(= \displaystyle \frac{\tan{\widehat{BAC}} + \tan30^o}{1 \ – \ \tan{\widehat{BAC}}. \tan30^o} = \displaystyle \frac{\displaystyle \frac{3}{4} + \displaystyle \frac{\sqrt{3}}{3}}{1 \ – \ \displaystyle \frac{3}{4}. \displaystyle \frac{\sqrt{3}}{3}}\)
\(= \displaystyle \frac{9 + \sqrt{3}}{12 \ – \ 3\sqrt{3}} = \displaystyle \frac{9 + 4\sqrt{3}}{12 \ – \ 3\sqrt{3}} \approx 2,34\)
Xét tam giác \(ABD\) vuông tại \(B\) ta có:
\(\tan{\widehat{BAD}} = \displaystyle \frac{BD}{AB}\)
\(\Rightarrow BD = AB. \tan{\widehat{BAD}} = 4. 2,34 \approx 9,36\)
Suy ra \(CD = BD \ – \ BC \approx 9,36 \ – \ 3 = 6,36\)
\(\)
Bài \(8\). Trong Hình \(4\), pít-tông \(M\) của động cơ chuyển động tịnh tiến qua lại dọc theo xi-lanh làm quay trục khuỷu \(IA\). Ban đầu \(I, A, M\) thẳng hàng. Cho \(\alpha\) là góc quay của trục khuỷu, \(O\) là vị trí của pít-tông khi \(\alpha = \displaystyle \frac{\pi}{2}\) và \(H\) là hình chiếu của \(A\) lên \(Ix\). Trục khuỷu \(IA\) rất ngắn so với độ dài thanh truyền \(AM\) nên có thể xem như độ dài \(MH\) không đổi và gần bằng \(MA\).
\(a)\) Biết \(IA = 8\) cm, viết công thức tính toạ độ \(x_M\) của điểm \(M\) trên trục \(Ox\) theo \(\alpha\).
\(b)\) Ban đầu \(\alpha = 0^o\). Sau \(1\) phút chuyển động, \(x_M = \ – \ 3\) cm. Xác định \(x_M\) sau \(2\) phút chuyển động. Làm tròn kết quả đến hàng phần mười.
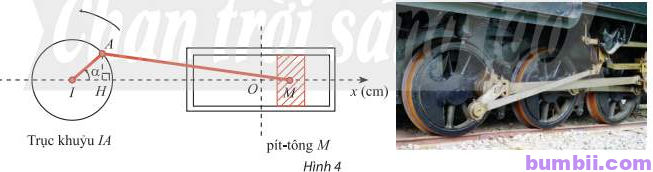
Trả lời:
\(a)\) Khi \(\alpha = \displaystyle \frac{\pi}{2}\) thì \(H \equiv I, M \equiv O\)
Mà \(3\) điểm \(I, A, M\) thẳng hàng.
Suy ra \(IH = OM\)
Pit-tông \(M\) chuyển động tịnh tiến qua lại dọc theo xi-lanh nên \(OM = x_M\)
Xét tam giác \(AHI\) vuông tại \(H\) ta có:
\(IH = IA. \cos{\alpha} = 8\cos{\alpha}\)
\(\Rightarrow x_M = 8\cos{\alpha}\)
\(b)\) Ở \(t = 0\) thì \(\alpha = 0\)
Khi \(t = 1\) thì \(x_M = \ – \ 3\) nên suy ra:
\(\cos{\alpha} = \displaystyle \frac{\ – \ 3}{8}\)
\(\Rightarrow \alpha \approx 112^o\)
Vậy sau \(2\) phút thì ta có \(\alpha = 112^o. 2 = 224^o\)
Khi đó \(x_M = 8 \cos224^o \approx \ – \ 5,8\) (cm)
Vậy sau \(2\) phút chuyển động thì \(x_M = \ – \ 5,8\)cm.
\(\)
Bài \(9\). Trong Hình \(5\), ba điểm \(M, N, P\) nằm ở đầu các cánh quạt của tua-bin gió. Biết các cánh quạt dài \(31\) m, độ cao của điểm \(M\) so với mặt đất là \(30\) m, góc giữa các cánh quạt là \(\displaystyle \frac{2\pi}{3}\) và số đo góc \((OA, OM) = \alpha\).
\(a)\) Tính \(\sin{\alpha} \text{ và } \cos{\alpha}\).
\(b)\) Tính \(\sin\) của các góc lượng giác \((OA, ON) \text{ và } (OA, OP)\), từ đó tính chiều cao của các điểm \(N\) và \(P\) so với mặt đất (theo đơn vị mét). Làm tròn kết quả đến hàng phần trăm.

Trả lời:
\(a)\) Gọi \(H, K\) lần lượt là hình chiếu vuông góc của điểm \(M\) lên trục \(Ox, Oy\)
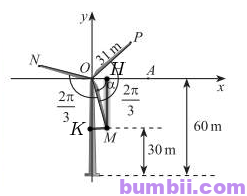
Khi đó ta có: \(MH = 60 \ – \ 30 = 30\) (m)
Xét tam giác \(MOH\) vuông tại \(H\) ta có:
\(\sin{\alpha} = \displaystyle \frac{MH}{OM} = \displaystyle \frac{\ – \ 30}{31}\)
\(\Rightarrow \cos{\alpha} = \sqrt{1 \ – \ \left(\ – \ \displaystyle \frac{30}{31}\right)^2} = \displaystyle \frac{\sqrt{61}}{31}\)
\(b)\) Vì góc giữa các cánh quạt là \(\displaystyle \frac{2\pi}{3}\) nên ta có:
\(\widehat{MON} = \widehat{MOP} = \widehat{NOP} = 120^o\)
Suy ra \(\widehat{AOP} = \widehat{MOP} \ – \ \widehat{AOP} = \widehat{MOP} \ – \ \alpha\)
\(\Rightarrow \sin{\widehat{AOP}} = \sin{\left(\widehat{MOP} \ – \ \alpha\right)}\)
\(= \sin{\widehat{MOP}}\cos{\alpha} \ – \ \cos{\widehat{MOP}} \sin{\alpha}\)
\(= \sin{\displaystyle \frac{2\pi}{3}}\cos{\alpha} \ – \ \cos{\displaystyle \frac{2\pi}{3}}\sin{\alpha}\)
\(= \displaystyle \frac{\sqrt{3}}{2}. \displaystyle \frac{\sqrt{61}}{31} + \displaystyle \frac{1}{2}. \displaystyle \frac{30}{31}\)
\(= \displaystyle \frac{30 + \sqrt{183}}{62} \approx 0,7\)
Vậy chiều cao của điểm \(P\) so với mặt đất là:
\(31. \sin{\widehat{AOP}} + 60 = 31. 0,7 + 60 = 81,7\) (m)
Ta có: \(\cos{\widehat{AOP}} = \sqrt{1 \ – \ \sin^2{\widehat{AOP}}} = \sqrt{1 \ – \ 0,7^2} \approx 0,71\)
Lại có: \(\widehat{AON} = \widehat{AOP} + \widehat{NOP}\)
Suy ra:
\(\sin{\widehat{AON}} = \sin{(\widehat{AOP} + \widehat{NOP})}\)
\( = \sin{\widehat{AOP}}\cos{\widehat{NOP}} + \cos{\widehat{AOP}} \sin{\widehat{NOP}}\)
\(= 0,7. \cos{\displaystyle \frac{2\pi}{3}} + 0,71. \sin{\displaystyle \frac{2\pi}{3}} = 0,7. \displaystyle \frac{\ – \ 1}{2} + 0,71. \displaystyle \frac{\sqrt{3}}{2}\)
\(\approx 0,26\)
Vậy chiều cao của điểm \(N\) so với mặt đất là:
\(31. \sin{\widehat{AON}} + 60 \approx 31. 0,26 + 60 = 68,06\) (m)
Bài 3. Các công thức lượng Bài 3. Các công thức lượng Bài 3. Các công thức lượng Bài 3. Các công thức lượng
Xem bài giải trước: Bài 2 – Giá trị lượng giác của một góc lượng giác
Xem bài giải tiếp theo:
Xem các bài giải khác: Giải bài tập SGK Toán Lớp 11 Chân trời sáng tạo
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech

Hạnh phúc đạt được khi bạn ngừng chờ đợi điều đó xảy ra và thực hiện các bước để biến nó thành hiện thực.