Chương 7 – Bài 28: Phép chia đa thức một biến trang 34 sách bài tập toán lớp 7 tập 2 NXB Kết nối tri thức với cuộc sống.
7.25. Tìm số tự nhiên n sao cho đa thức \(1,2x^5-3x^4 + 3,7x^2\) chia hết cho \(x^n.\)
Giải
Đa thức đã cho chia hết cho \(x^n\) nếu từng hạng tử của nó chia hết cho \(x^n,\) nói riêng là \(3,7x^2\) chia hết cho \(x^n.\) Điều này xảy ra khi \(n ≤ 2.\)
Mà n là số tự nhiên nên n ∈ {0; 1; 2}.
\(\)
7.26. Thực hiện các phép chia sau:
a) \((-4x^5 + 3x^3-2x^2) : (-2x^2);\)
b) \((0,5x^3-1,5x^2 + x) : 0,5x;\)
c) \((x^3 + 2x^2-3x + 1) : \displaystyle\frac{1}{3}x^2.\)
Giải
a) \((-4x^5 + 3x^3-2x^2) : (-2x^2)\)
\(= (-4x^5) : (-2x^2) + (3x^3) : (-2x^2)\) \(+ (-2x^2) : (-2x^2)\)
\(= 2x^3-1,5x + 1.\)
b) \((0,5x^3-1,5x^2 + x) : 0,5x\)
\(= 0,5x^3 : 0,5x + (-1,5x^2) : 0,5x\) \(+ x : 0,5x\)
\(= x^2-3x + 2.\)
c) \((x^3 + 2x^2-3x + 1) : \displaystyle\frac{1}{3}x^2\)
Ta có thể viết : \(x^3 + 2x^2-3x + 1\) \(= (3x + 6) \displaystyle\frac{1}{3}x^2 + (-3x + 1).\)
Do đa thức \(-3x + 1\) có bậc là \(1,\) nhỏ hơn bậc \(2\) của đa thức chia nên đẳng thức này chứng tỏ \(3x + 6\) là thương và \(-3x + 1\) là dư trong phép chia đã cho.
\(\)
7.27. Đặt tính và làm phép chia sau:
a) \((x^3-4x^2-x + 12) : (x-3);\)
b) \((2x^4-3x^3 + 3x^2 + 6x-14) : (x^2-2).\)
Giải
a) \((x^3-4x^2-x + 12) : (x-3)\)
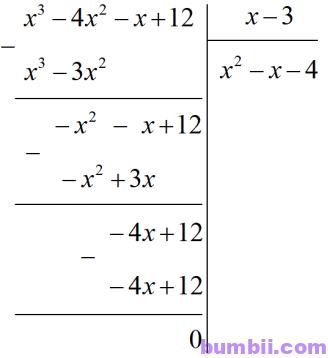
Vậy \((x^3-4x^2-x + 12) : (x-3)=x^2-x -4.\)
b) \((2x^4-3x^3 + 3x^2 + 6x-14) : (x^2-2)\)

Vậy \((2x^4-3x^3 + 3x^2 + 6x-14) : (x^2-2)\) \(=2x^2-3x + 7.\)
\(\)
7.28. Khi làm phép chia \((6x^3-7x^2-x + 2) : (2x + 1),\) bạn Quỳnh cho kết quả đa thức dư là \(4x + 2.\)
a) Không làm phép chia, hãy cho biết bạn Quỳnh đúng hay sai, tại sao?
b) Tìm thương và dư trong phép chia đó.
Giải
a) Quỳnh sai. Vì bậc của đa thức dư, nếu khác 0, phải nhỏ hơn bậc của đa thức chia.
b) \((6x^3-7x^2-x + 2) : (2x + 1)\)
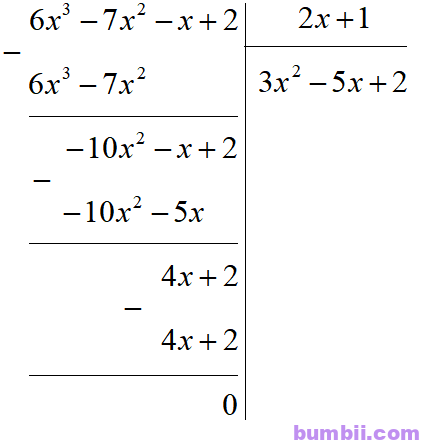
Vậy \((6x^3-7x^2-x + 2) : (2x + 1)\) \(=3x^2-5x + 2\)
\(\)
7.29. Cho hai đa thức \(A = 3x^4 + x^3 + 6x-5\) và \(B = x^2 + 1.\) Tìm thương Q và dư R trong phép chia A cho B rồi kiểm nghiệm lại rằng A = BQ + R.
Giải
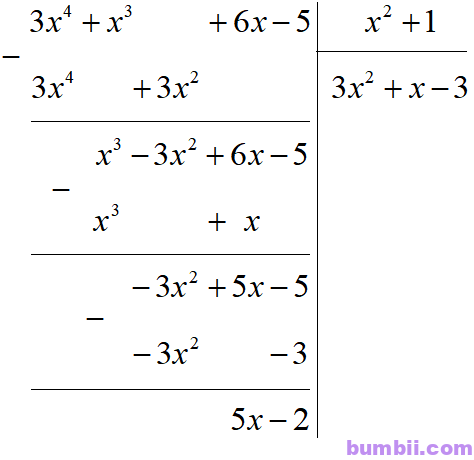
Vậy phép chia A cho B ta được thương là \(Q = 3x^2 + x-3\) và dư \(R = 5x-2.\)
Kiểm nghiệm \(BQ + R = (x^2 + 1)(3x^2 + x-3) + 5x-2\)
\(= x^2( 3x^2 + x-3) + 1. (3x^2 + x-3) + 5x-2\)
\(= 3x^4 + x^3-3x^2 + 3x^2 + x-3 + 5x-2\)
\(= 3x^4 + x^3 + (-3x^2 + 3x^2) + (x + 5x) + (-3-2)\)
\(= 3x^4 + x^3 + 6x-5 = A\)
Vậy A = BQ + R là một đẳng thức đúng.
\(\)
7.30. Thực hiện các phép chia sau:
a) \((2x^4 + x^3-3x^2 + 5x-2) : (x^2-x + 1);\)
b) \((x^4-x^3-x^2 + 3x) : (x^2-2x +3).\)
Giải
a) \((2x^4 + x^3-3x^2 + 5x-2) : (x^2-x + 1)\)

Vậy \((2x^4 + x^3-3x^2 + 5x-2) : (x^2-x + 1)\) \(=2x^2 +3x-2\).
b) \((x^4-x^3-x^2 + 3x) : (x^2-2x +3)\)

Vậy \((x^4-x^3-x^2 + 3x) : (x^2-2x +3)\) \(=x^2 +x-2\) (dư \(-4x+6\)).
\(\)
7.31. Cho đa thức \(A(x) = 3x^4 + 11x^3-5x^2-19x-5.\) Tìm đa thức \(H(x)\) sao cho:
\(A(x) = (3x^2 + 2x-5).H(x)\)
Giải
Ta có \(A(x) = (3x^2 + 2x-5).H(x)\)
\(H(x) = A(x) : (3x^2 + 2x-5) = (3x^4 + 11x^3\) \(-5x^2-19x-5) : (3x^2 + 2x-5)\)
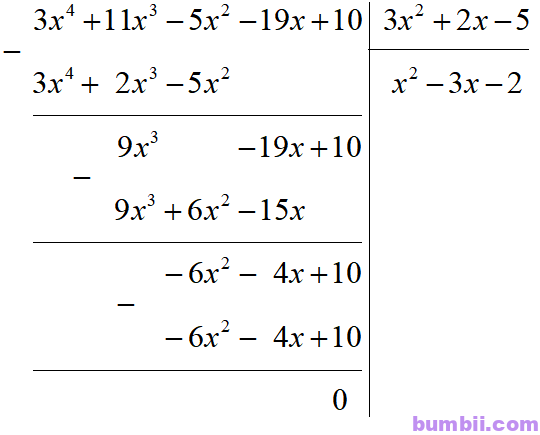
Vậy \(H(x) = x^2 + 3x-2.\)
\(\)
7.32. Tìm số m sao cho đa thức \(P(x) = 2x^3-3x^2 + x + m\) chia hết cho đa thức \(x + 2.\)
Giải
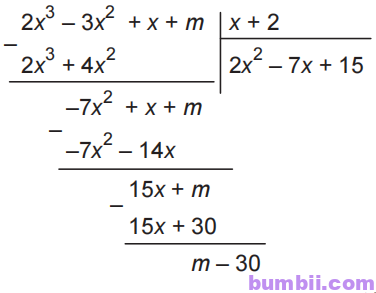
Để phép chia này là phép chia hết thì \(m – 30 = 0.\)
Vậy \(m = 30.\)
\(\)
7.33. Cho đa thức P(x). Chứng minh rằng:
a) Nếu P(x) chia hết cho x – a thì a là một nghiệm của đa thức P(x).
b) Nếu x = a là một nghiệm của đa thức P(x) thì P(x) chia hết cho x – a.
Giải
a) Giả sử P(x) chia hết cho x-a. Gọi Q(x) là đa thức thương, ta có:
P(x) = (x – a)Q(x) (1)
Từ đẳng thức (1), ta có P(a) = (a – a)Q(a) = 0.
Vậy a là một nghiệm của P(x).
b) Ngược lại, cho a là một nghiệm của P(x). Giả sử chia P(x) cho x – a, ta được thương là Q(x) và dư là R(x), nghĩa là ta có:
P(x) = (x – a)Q(x) + R(x) (2)
Trong đó hoặc R(x) = 0, hoặc nếu R(x) ≠ 0 thì R(x) phải có bậc nhỏ hơn bậc của đa thức x – a, tức là nhỏ hơn 1.
Sau đây, ta sẽ chứng tỏ rằng chỉ có thể xảy ra R(x) = 0.
Thật vậy, nếu R(x) ≠ 0 thì do bậc của R(x) nhỏ hơn 1 nên R(x) có bậc 0. Nói cách khác, R(x) là một số khác 0 nào đó. Nhưng điều đó là vô lí vì khi đó đẳng thức (2) không thể xảy ra, chẳng hạn khi x = a thì vế trái bằng 0 trong khi vế phải khác 0.
Vậy chỉ có thể xảy ra R(x) = 0, nghĩa là P(x) chia hết cho x – a.
\(\)
Xem bài giải trước: Bài 27: Phép nhân đa thức một biến
Xem bài giải tiếp theo: Ôn tập chương VII
Xem thêm các bài giải khác tại: Giải Bài tập Toán Lớp 7 – NXB Kết Nối Tri Thức Với Cuộc Sống
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech
