Chương 5 – Bài 2. Tứ giác trang 100 sách giáo khoa toán lớp 8 tập 1 Cánh Diều. Các em cùng Bumbii giải các bài tập sau.
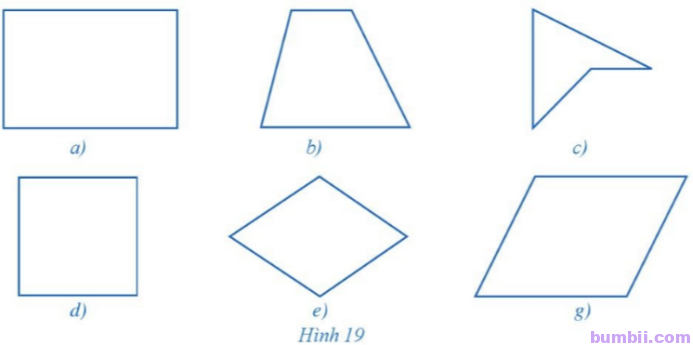
1. Trong các tứ giác ở hình 19a, 19b, 19c, 19d, 19e, 19g, tứ giác nào không phải là tứ giác lồi? Vì sao?
Giải
Tứ giác ở hình 19c không phải là tứ giác lồi vì tứ giác này nằm khác phía của đường thẳng chứa một cạnh của tứ giác đó.
\(\)
2. a) Tứ giác ABCD có \(\widehat{A} +\widehat{C} =180^o\) thì \(\widehat{B} +\widehat{D}\) bằng bao nhiêu độ?
b) Có hay không một tứ giác có 2 góc tù và 2 góc vuông?
c) Có hay không một tứ giác có cả 4 góc đều là góc nhọn?
Giải
a) Trong tứ giác ABCD, ta có \(\widehat{A} +\widehat{B} +\widehat{C} +\widehat{D} =360^o.\)
Suy ra \(\widehat{B} +\widehat{D} =360^o-(\widehat{A} +\widehat{C})\) \(=360^o-180^o=180^o.\)
Vậy \(\widehat{B} +\widehat{D} =180^o.\)
b) Giả sử tứ giác ABCD có \(\widehat{A},\ \widehat{B} = 90^o.\) và \(\widehat{C},\ \widehat{D} > 90^o.\)
Ta có: \(\widehat{A} +\widehat{B} +\widehat{C} +\widehat{D} >90^o+90^o+90^o+90^o=360^o\)
Mà tổng các góc trong một tứ giác bằng \(360^o\) nên không có một tứ giác có 2 góc tù và 2 góc vuông.
c) Giả sử tứ giác ABCD có \(\widehat{A},\ \widehat{B},\ \widehat{C},\ \widehat{D} < 90^o.\)
Ta có: \(\widehat{A} +\widehat{B} +\widehat{C} +\widehat{D} <90^o+90^o+90^o+90^o=360^o\)
Mà tổng các góc trong một tứ giác bằng \(360^o\) nên không có một tứ giác có cả 4 góc đều là góc nhọn.
\(\)
3. Hình 20 mô tả mặt cắt dọc phân nổi trên mặt nước của một chiếc tàu thuỷ. Tính chu vi mặt cắt dọc phân nổi trên mặt nước của chiếc tàu thuỷ đó (làm tròn kết quả đến hàng phần mười của mét).
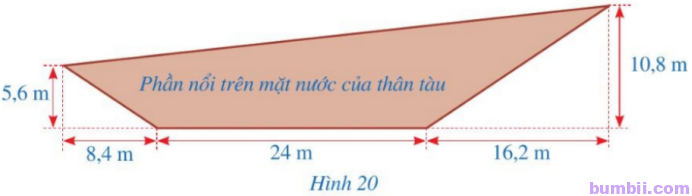
Giải
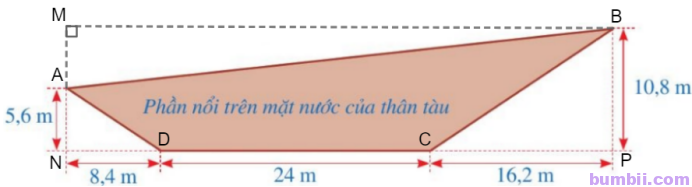
Do tam giác AMB vuông tại M nên theo định lí Pythagore ta có:\(AB^2 = AM^2 + MB^2\)
Suy ra \(AB^2= (10,8-5,6)^2 + (8,4+24+16,2)^2\) \(= 27,04 + 2361,96 = 2389.\)
Do đó \(BC=\sqrt{2389}\) (m).
Do tam giác AND vuông tại N nên theo định lí Pythagore ta có:\(AD^2 = AN^2 + ND^2\)
Suy ra \(AD^2= 5,6^2 + 8,4^2\) \(= 31,36 + 70,56 = 101,92.\)
Do đó \(AD=\sqrt{101,92}\) (m).
Do tam giác BPC vuông tại P nên theo định lí Pythagore ta có:\(BC^2 = BP^2 + CP^2\)
Suy ra \(BC^2= 10,8^2 + 16,2^2\) \(= 262,44 + 116,64 = 379,08.\)
Do đó \(BC=\sqrt{379,08}\) (m).
Chu vi mặt cắt dọc phần nổi trên mặt nước của chiếc tàu thuỷ đó là:
\(AB + BC + CD + DA\) \(= \sqrt{2389}+\sqrt{379,08}+24+\sqrt{101,92}≈ 102,4 \) (m).
\(\)
Xem bài giải trước: Bài 1. Định lí Pythagore
Xem bài giải tiếp theo: Bài 3. Hình thang cân
Xem thêm các bài giải khác tại: Giải bài tập SGK Toán Lớp 8 Cánh Diều
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech
