Bài \(15\). Giới hạn của dãy số trang \(104\) SGK Toán lớp \(11\) tập \(1\) Kết nối tri thức với cuộc sống. Các em cùng Bumbii giải các bài tập sau:
Bài \(5.1\). Tìm các giới hạn sau:
\(a)\) \(\displaystyle \lim_{n \to + \infty} \frac{n^2 + n + 1}{2n^2 + 1}\).
\(b)\) \(\lim \limits_{n \to + \infty} {(\sqrt{n^2 + 2n} \ – \ n)}\).
Trả lời:
\(a)\) \(\displaystyle \lim_{n \to +\infty} \frac{n^2 + n + 1}{2n^2 + 1} = \displaystyle \lim_{n \to +\infty} \frac{1 + \frac{1}{n} + \frac{1}{n^2}}{2 + \frac{1}{n^2}}\)
\(= \displaystyle \frac{\lim \limits_{n \to +\infty} \left(1 + \displaystyle \frac{1}{n} + \displaystyle \frac{1}{n^2}\right)}{\lim \limits_{n \to +\infty} \left(2 + \frac{1}{n^2}\right)}\)
\(= \displaystyle \frac{1}{2}\).
\(b)\) \(\lim \limits_{n \to +\infty} (\sqrt{n^2 + 2n} \ – \ n) = \displaystyle \lim_{n \to +\infty} \frac{n^2 + 2n \ – \ n^2}{\sqrt{n^2 + 2n} + n}\)
\(= \displaystyle \lim_{n \to +\infty} \frac{2n}{n\left(\sqrt{1 + \frac{2}{n}} + 1\right)} = \displaystyle \lim_{n \to +\infty} \frac{2}{\sqrt{1 + \frac{2}{n}} + 1}\)
\(= \displaystyle \frac{2}{1 + 1} = 1\)
\(\)
Bài \(5.2\). Cho hai dãy số không âm \((u_n)\) và \((v_n)\) với \(\lim \limits_{n \to + \infty} u_n = 2\) và \(\lim \limits_{n \to + \infty} v_n = 3\). Tìm các giới hạn sau:
\(a)\) \(\displaystyle \lim_{n \to +\infty} \frac{u_n^2}{v_n \ – \ u_n}\).
\(b)\) \(\lim \limits_{n \to +\infty} \sqrt{u_n + 2v_n}\).
Trả lời:
\(a)\) \(\displaystyle \lim_{n \to +\infty} \frac{u_n^2}{v_n \ – \ u_n} = \displaystyle \frac{(\lim \limits_{n \to +\infty} u_n)^2}{\lim \limits_{n \to +\infty} v_n \ – \ \lim \limits_{n \to +\infty} u_n}\)
\(= \displaystyle \frac{2^2}{3 \ – \ 2} = 4\)
\(b)\) Ta có: \(\lim \limits_{n \to +\infty} (u_n + 2v_n) = \lim \limits_{n \to +\infty} u_n + 2 \lim \limits_{n \to +\infty} v_n\)
\(= 2 + 2. 3 = 8\)
Suy ra \(\lim \limits_{n \to +\infty} \sqrt{u_n + 2v_n} = \sqrt{8} = 2\sqrt{2}\)
\(\)
Bài \(5.3\). Tìm giới hạn của các dãy số cho bởi:
\(a)\) \(u_n = \displaystyle \frac{n^2 + 1}{2n \ – \ 1}\).
\(b)\) \(v_n = \sqrt{2n^2 + 1} \ – \ n\).
Trả lời:
\(a)\) \(\lim \limits_{n \to +\infty} u_n = \displaystyle \lim_{n \to +\infty} \frac{n^2 + 1}{2n \ – \ 1}\)
\(= \displaystyle \lim_{n \to +\infty} \frac{1 + \frac{1}{n^2}}{\frac{2}{n} \ – \ \frac{1}{n^2}}\)
\(= \displaystyle \frac{\lim \limits_{n \to +\infty} \left(1 + \frac{1}{n^2}\right)}{\lim \limits_{n \to +\infty} \left(\frac{2}{n} \ – \ \frac{1}{n^2}\right)}\)
Ta có: \(\lim \limits_{n \to +\infty} \left(1 + \displaystyle \frac{1}{n^2}\right) = 1\)
\(\lim \limits_{n \to +\infty} \left(\displaystyle \frac{2}{n} \ – \ \displaystyle \frac{1}{n^2}\right) = 0\)
Suy ra \(\lim \limits_{n \to +\infty} u_n = +\infty\)
\(b)\) \(\lim \limits_{n \to +\infty} v_n = \lim \limits_{n \to + \infty} (\sqrt{2n^2 + 1} \ – \ n)\)
\(= \displaystyle \lim_{n \to +\infty} \frac{2n^2 + 1 \ – \ n^2}{\sqrt{2n^2 + 1} + n}\)
\( = \displaystyle \lim_{n \to +\infty} \frac{n^2 +1}{n^2 \left(\sqrt{\frac{2}{n^2} + \frac{1}{n^4}} + \frac{1}{n}\right)}\)
\(= \displaystyle \lim_{n \to +\infty} \frac{1 + \frac{1}{n^2}}{\sqrt{\frac{2}{n^2} + \frac{1}{n^4}} + \frac{1}{n}}\)
\(= +\infty\)
\(\)
Bài \(5.4\). Viết các số thập phân vô hạn tuần hoàn sau đây dưới dạng phân số:
\(a)\) \(1,(12) = 1,121212….\);
\(b)\) \(3,(102) = 3,102102102…\).
Trả lời:
\(a)\) Ta có: \(1,121212… = 1 + 0,12 + 0,0012 + 0,000012 + ….\)
\(= 1 + 12. 10^{\ – \ 2} + 12. 10^{\ – \ 4} + 12. 10^{\ – \ 6} + …\)
Lại có: \(12. 10^{\ – \ 2} + 12. 10^{\ – \ 4} + 12. 10^{\ – \ 6} + …\) là tổng cấp số nhân lùi vô hạn với \(u_1 = 12. 10^{\ – \ 2}, q = 10^{\ – \ 2}\) nên ta được:
\(1,121212… = 1 + \displaystyle \frac{u_1}{1 \ – \ q} \)
\(= 1 + \displaystyle \frac{12. 10^{\ – \ 2}}{1 \ – \ 10^{\ – \ 2}} = \displaystyle \frac{37}{33}\).
\(b)\) \(3,102102102… = 3 + 0,102 + 0,000102 + 0,000000102 + …\)
\(= 3 + 102. 10^{\ – \ 3} + 102. 10^{\ – \ 6} + 102. 10^{\ – \ 9} + …\)
Ta có: \(102. 10^{\ – \ 3} + 102. 10^{\ – \ 6} + 102. 10^{\ – \ 9} + …\) là tổng cấp số nhân lùi vô hạn với \(u_1 = 102. 10^{\ – \ 3}, q = 10^{\ – \ 3}\) nên ta được:
\(3,102102102… = 3 + \displaystyle \frac{u_1}{1 \ – \ q}\)
\(= 3 + \displaystyle \frac{102. 10^{\ – \ 3}}{1 \ – \ 10^{\ – \ 3}} = \displaystyle \frac{1033}{333}\)
\(\)
Bài \(5.5\). Một bệnh nhân hàng ngày phải uống một viên thuốc \(150\) mg. Sau ngày đầu, trước mỗi lần uống, hàm lượng thuốc cũ trong cơ thể vẫn còn \(5 \%\). Tính lượng thuốc có trong cơ thể sau khi uống xong viên thuốc của ngày thứ (5\). Ước tính lượng thuốc trong cơ thể nếu bệnh nhân sử dụng thuốc trong một thời gian dài.
Trả lời:
Lượng thuốc trong cơ thể bệnh nhân sau khi uống viên thuốc của ngày đầu tiên là \(150\) mg.
Sau ngày đầu, trước mỗi lần uống, hàm lượng thuốc cũ trong cơ thể vẫn còn \(5 \%\) nên tổng lượng thuốc trong cơ thể bệnh nhân sau khi uống viên thuốc của ngày thứ hai là:
\(150 + 150. 5 \% = 150 (1 + 0,05)\) (mg)
Lượng thuốc trong cơ thể bệnh nhân sau khi uống viên thuốc của ngày thứ ba là:
\(150 + 150 (1 + 0,05). 5 \% = 150 + 150 (1 + 0,05). 0,05\)
\(= 150(1 + 0,05 + 0,05^2)\) (mg)
Tương tự ta có:
Lượng thuốc trong cơ thể bệnh nhân sau khi uống viên thuốc của ngày thứ tư là: \(= 150(1 + 0,05 + 0,05^2 + 0,05^3)\) (mg)
Lượng thuốc trong cơ thể bệnh nhân sau khi uống viên thuốc của ngày thứ năm là:
\(= 150(1 + 0,05 + 0,05^2 + 0,05^3 + 0,05^4) = 157,8946875\) (mg)
Lượng thuốc trong cơ thể bệnh nhân nếu bệnh nhân sử dụng thuốc trong thời gian dài là:
\(S = 150(1 + 0,05 + 0,05^2 + 0,05^3 + 0,05^4 + …)\) (mg)
Mặt khác, \(1 + 0,05 + 0,05^2 + 0,05^3 + 0,05^4 + …\) là tổng của cấp số nhân lùi vô hạn với số hạng đầu \(u_1 = 1\), công bội \(q = 0,05\)
Do đó \(1 + 0,05 + 0,05^2 + 0,05^3 + 0,05^4 + … \)
\(= \displaystyle \frac{u_1}{1 \ – \ q} = \displaystyle \frac{1}{1 \ – \ 0,05} = \displaystyle \frac{20}{19}\)
Suy ra \(S = 150. \displaystyle \frac{20}{19} = \displaystyle \frac{400}{361}\)
Vậy lượng thuốc trong cơ thể bệnh nhân nếu bệnh nhân sử dụng thuốc trong thời gian dài là \(\displaystyle \frac{400}{361}\) mg.
\(\)
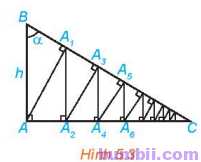
Bài \(5.6\). Cho tam giác vuông \(ABC\) vuông tại \(A\), có \(AB = h\) và góc \(B\) bằng \(\alpha\) (\(H.5.3\)). Từ \(A\) kẻ \(AA_1 \perp BC\), từ \(A_1\) kẻ \(A_1A_2 \perp AC\), sau đó lại kẻ \(A_2A_3 \perp BC\). Tiếp tục quá trình trên ta được đường gấp khúc vô hạn \(AA_1A_2A_3…\). Tính độ dài đường gấp khúc này theo \(h\) và \(\alpha\).
Trả lời:
Tam giác \(AA_1B\) vuông tại \(A\) nên \(AA_1 = h. \sin{\alpha}\)
Có \(\widehat{B} + \widehat{A_1AB} = 90^o\)
Lại có: \(\widehat{A_1AA_2} + \widehat{A_1AB} = 90^o\)
Suy ra \(\widehat{A_1AA_2} = \alpha\)
Tam giác \(A_1AA_2\) vuông tại \(A_2\) nên ta có:
\(A_1A_2 = AA_1 \sin{\alpha} = h \sin^2{\alpha}\)
Tam giác \(A_1A_2A_3\) vuông tại \(A_3\) có \(\widehat{A_2A_1A_3} = \alpha\) nên ta có:
\(A_2A_3 = A_1A_2. \sin{\alpha} = h \sin^3{\alpha}\)
Tương tự như vậy, ta xác định được \(A_{n \ – \ 1}A_n = h \sin^n{\alpha}\)
Khi đó độ dài đường gấp khúc là:
\(AA_1A_2A_3… = AA_1 + A_1A_2 + A_2A_3 +…. + A_{n \ – \ 1}A_n + …\)
\(= h\sin{\alpha} + h \sin^2{\alpha} + h \sin^3{\alpha} + … + h \sin^n{\alpha} + ..\)
Do góc \(B\) là góc nhọn nên ta có \(0 \leq \sin{B} = \sin{\alpha} < 1\), suy ra \(|\sin{\alpha}| < 1\)
Khi đó, độ dài của đường gấp khúc vô hạn \(AA_1A_2A_3…\) là tổng của cấp số nhân lùi vô hạn với số hạng đầu \(u_1 = h\sin{\alpha}\) và công bội \(q = \sin{\alpha}\)
Vậy \(AA_1A_2A_3… = \displaystyle \frac{u_1}{1 \ – \ q} = \displaystyle \frac{h\sin{\alpha}}{1 \ – \ \sin{\alpha}}\)
\(\)
Xem bài giải trước: Bài tập cuối chương IV
Xem bài giải tiếp theo: Bài 16 – Giới hạn của hàm số
Xem các bài giải khác: Giải bài tập SGK Toán Lớp 11 Kết nối tri thức với cuộc sống
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech

Hạnh phúc đạt được khi bạn ngừng chờ đợi điều đó xảy ra và thực hiện các bước để biến nó thành hiện thực.