Bài \(1\). Hai đường thẳng vuông góc trang \(54\) Sách giáo khoa Toán lớp \(11\) tập \(2\) Chân trời sáng tạo. Các em cùng Bumbii giải các bài tập sau:
Bài \(1\). Cho hình chóp \(S.ABCD\) có đáy là hình thoi \(ABCD\) cạnh \(a\). Cho biết \(SA = a\sqrt{3}, SA \perp AB \text{ và } SA \perp AD\). Tính góc giữa \(SB\) và \(CD\), \(SD\) và \(CB\).
Trả lời:
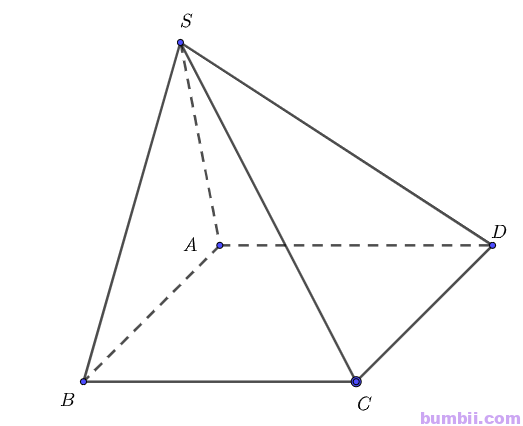
Ta có: \(CD // AB\) suy ra \((SB, CD) = (SB, AB) = \widehat{SBA}\)
Xét tam giác \(SAB\) vuông tại \(A\) có:
\(\tan{\widehat{SBA}} = \displaystyle \frac{SA}{AB} = \displaystyle \frac{a\sqrt{3}}{a} = \sqrt{3}\)
\(\Rightarrow \widehat{SBA} = 60^o\)
\(\Rightarrow (SB, CD) = 60^o\)
Lại có \(CB // DA\) suy ra \((SD, CB) = (SD, DA) = \widehat{SDA}\)
Xét tam giác \(SAD\) vuông tại \(A\) có \(SA = a\sqrt{3}, AD = a\) nên \(\widehat{SDA} = 60^o\)
\(\Rightarrow (SD, CB) = 60^o\)
\(\)
Bài \(2\). Cho tứ diện đều \(ABCD\). Chứng minh rằng \(AB \perp CD\)
Trả lời:
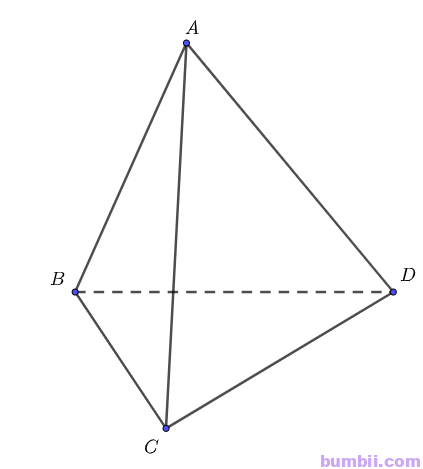
Ta có: \(\overrightarrow{AB}. \overrightarrow{CD} = \overrightarrow{AB}. (\overrightarrow{AD} \ – \ \overrightarrow{AC})\)
\(= \overrightarrow{AB}. \overrightarrow{AD} \ – \ \overrightarrow{AB}. \overrightarrow{AC}\)
\(= AB. AD. \cos{\widehat{BAD}} \ – \ AB. AC. \cos{\widehat{BAC}}\)
\(= 0\) (Do tứ diện đều nên \(AB = AC = AD \text{ và } \widehat{BAC} = \widehat{BAD}\))
Suy ra \(AB \perp CD\) (đpcm)
\(\)
Bài \(3\). Cho hình chóp \(S.ABC\) có \(SA = SB = SC = a, \widehat{BSA} = \widehat{CSA} = 60^o, \widehat{BSC} = 90^o\). Cho \(I\) và \(J\) lần lượt là trung điểm của \(SA\) và \(BC\). Chứng minh rằng \(IJ \perp SA\) và \(IJ \perp BC\).
Trả lời:
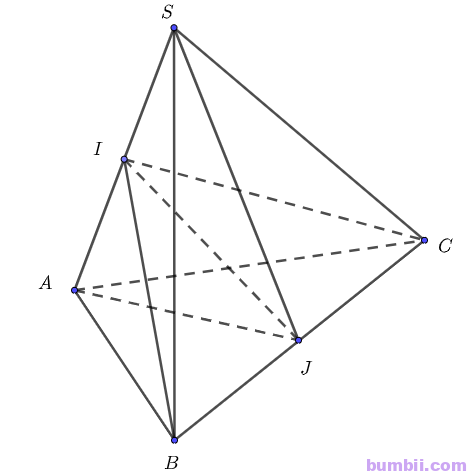
Tam giác \(SAC\) có \(SA = SC = a, \widehat{CSA} = 60^o\) nên tam giác \(SAC\) đều
\(\Rightarrow AC = a\)
Tương tự tam giác \(SAB\) đều nên \(AB = a\)
Xé hai tam giác \(ABC\) và \(SBC\) có:
\(\begin{equation} \left.\begin{array}{II} BC \text{ chung }\\AB = SB = a\\AC = SC = a \end{array} \right \} \end{equation} \Rightarrow \Delta_{ABC} = \Delta_{SBC}\)
Suy ra hai trung tuyến \(AJ = SJ\) hay tam giác \(SJA\) cân tại \(J\)
Khi đó trung tuyến \(IJ\) đồ(ng thời là đường cao.
\(\Rightarrow IJ \perp SA\) (đpcm)
Xét hai tam giác \(SAB\) và \(SAC\) có:
\(\begin{equation} \left.\begin{array}{II} SA \text{ chung }\\SB = SC = a\\AB = AC= a \end{array} \right \} \end{equation} \Rightarrow \Delta_{SAB} = \Delta_{SAC}\)
Suy ra hai trung tuyến \(BI = CI\) hay tam giác \(BCI\) cân tại \(I\)
Khi đó trung tuyến \(IJ\) đồng thời là đường cao.
\(\Rightarrow IJ \perp BC\) (đpcm)
\(\)
Bài \(4\). Cho tứ diện đều \(ABCD\) cạnh \(a\). Gọi \(K\) là trung điểm của \(CD\). Tính góc giữa hai đường thằng \(AK\) và \(BC\).
Trả lời:
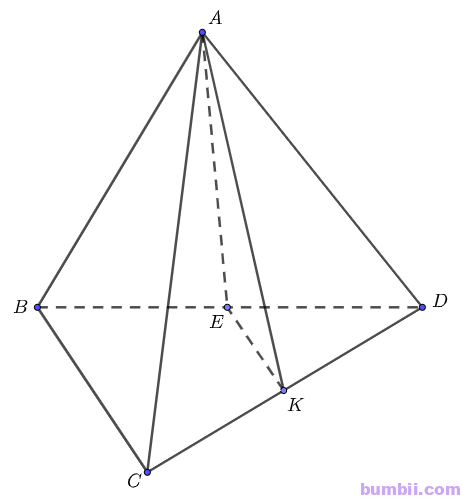
Qua \(K\) kẻ đường thẳng song song với \(BC\), cắt \(BD\) tại \(E\). Khi đó \(E\) là trung điểm của \(BD\)
\(\Rightarrow AK, AE\) lần lượt là đường trung tuyến đồng thời là đường cao trong tam giác đều \(ACD\) và \(ABD\).
Khi đó \((AK, BC) = (AK, KE) = \widehat{AKE}\)
Xét tam giác \(AKE\) có:
\(AK = AE = \displaystyle \frac{a\sqrt{3}}{2}\)
\(EK = \displaystyle \frac{1}{2} BC = \displaystyle \frac{a}{2}\)
Áp dụng định lý côsin trong tam giác \(AKE\) ta được: \(\cos{\widehat{AKE}} = \displaystyle \frac{AK^2 + KE^2 \ – \ AE^2}{2. AK. KE}\)
\(= \displaystyle \frac{KE^2}{2. AK. KE} = \displaystyle \frac{KE}{2. AK} = \displaystyle \frac{\displaystyle \frac{a}{2}}{2. \displaystyle \frac{a\sqrt{3}}{2}}\)
\(= \displaystyle \frac{1}{2\sqrt{3}}\)
\(\Rightarrow \widehat{AKE} \approx 73^o\)
Vậy góc giữa hai đường thẳng \(AK\) và \(BC\) là \(73^o\)
\(\)
Bài \(5\). Cho tứ diện (ABCD\). Gọi \(M, N\) lần lượt là trung điểm của \(BC\) và \(AD\). Biết \(AB = CD = 2a\) và \(MN = a\sqrt{3}\). Tính góc giữa \(AB\) và \(CD\).
Trả lời:
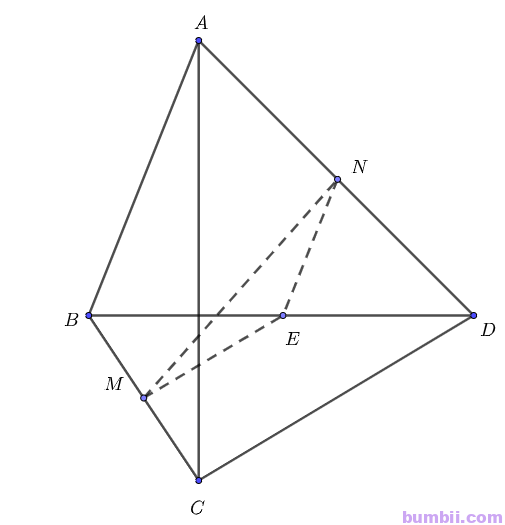
Qua \(M\) kẻ đường thẳng song song với \(CD\), cắt \(BD\) tại \(E\). Khi đó \(E\) là trung điểm của \(BD\)
\(\Rightarrow EN //AB\)
Suy ra \((AB, CD) = (ME, NE)\)
Ta có: \(AB = CD = 2a \Rightarrow ME = EN = a\)
Áp dụng định lí côsin trong tam giác \(MEN\) ta có: \(MN^2 = ME^2 + EN^2 \ – \ 2. ME. EN. \cos{\widehat{MEN}}\)
\(\Rightarrow \cos{\widehat{MEN}} = \displaystyle \frac{ME^2 + EN^2 \ – \ MN^2}{2. ME. EN}\)
\(= \displaystyle \frac{a^2 + a^2 \ – \ (a\sqrt{3})^2}{2. a. a} = \ – \ \displaystyle \frac{1}{2}\)
\(\Rightarrow \widehat{MEN} = 120^o\)
\(\Rightarrow (ME, NE) = 180^o \ – \ 120^o = 60^o\)
Vậy \((AB, CD) = 60^o\)
\(\)
Bài \(6\). Một ô che nắng có viền khung hình lục giác đều \(ABCDEF\) song song với mặt bàn và có cạnh \(AB\) song song với cạnh bàn \(a\) (Hình \(5\)). Tính số đo góc hợp bởi đường thẳng \(a\) lần lượt với các đường thẳng \(AF, AE\) và \(AD\).

Trả lời:
Số đo mỗi góc trong hình lục giác đều là \(120^o\)
Vì \(a // AB\) suy ra \((a, AF) = (AB, AF) = 180^o \ – \ \widehat{BAF}\)
\(= 180^o \ – \ 120^o = 60^o\)
(vì số đo góc giữa hai đường thẳng phải \(\leq 90^o\))
Xét tam giác \(AEF\) có \(\widehat{AFE} = 120^o, FE = FA\) suy ra \(\widehat{AEF} = \widehat{FAE} = 30^o\)
\(\widehat{BAF} = \widehat{BAE} + \widehat{FAE} = 120^o\)
\(\Rightarrow \widehat{BAE} = 120^o \ – \ 30^o = 90^o\)
Suy ra \((a, AE) = (AB, AE) = 90^o\)
\(ABCDEF\) là lục giác đều có \(AD\) là đường chéo
Suy ra \(\widehat{BAD} = 60^o\)
\(\Rightarrow (a, AD) = (AB, AD) = 60^o\)
Bài 1. Hai đường thẳng vuông góc Bài 1. Hai đường thẳng vuông góc Bài 1. Hai đường thẳng vuông góc
Xem bài giải trước: Bài tập cuối chương VII
Xem bài giải tiếp theo: Bài 2 – Đường thẳng vuông góc với mặt phẳng
Xem các bài giải khác: Giải bài tập SGK Toán Lớp 11 Chân trời sáng tạo
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech

Hạnh phúc đạt được khi bạn ngừng chờ đợi điều đó xảy ra và thực hiện các bước để biến nó thành hiện thực.