Chương 9 – Bài 32: Quan hệ giữa đường vuông góc và đường xiên trang 50 sách bài tập toán lớp 7 tập 2 NXB Kết nối tri thức với cuộc sống.
9.5. Cho hai đường thẳng song song c và d. Chứng minh rằng khoảng cách từ mọi điểm thuộc c đến đường thẳng d bằng nhau và bằng khoảng cách từ mọi điểm thuộc đường thẳng d đến đường thẳng c (khoảng cách đó được gọi là khoảng cách giữa hai đường thẳng song song c và d).
Giải
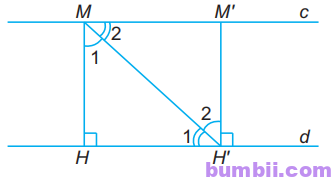
Lấy M, M’ thuộc đường thẳng c (M khác M’).
Kẻ MH, M’H’ vuông góc với đường thẳng d (H và H’ thuộc đường thẳng d).
Do MH \(\bot\) d và M’H’ \(\bot\) d nên MH // M’H’.
Xét hai tam giác MHH’ và H’M’M có:
MH’ là cạnh chung;
\(\widehat{M_1}=\widehat{H’_2}\) (so le trong);
\(\widehat{M_2}=\widehat{H’_1}\) (so le trong);
Do đó \(∆MHH’ = ∆H’M’M\) (g.c.g).
Suy ra MH = M’H’ (độ dài MH gọi là khoảng cách từ c đến d).
Vậy khoảng cách từ mọi điểm thuộc c đến đường thẳng d bằng nhau và bằng khoảng cách từ mọi điểm thuộc đường thẳng d đến đường thẳng c.
\(\)
9.6. Cho hai điểm phân biệt M, M’ ở cùng phía đối với đường thẳng d (M, M’ không thuộc d). Chứng minh rằng nếu M, M’ có cùng khoảng cách đến đường thẳng d thì MM’ song song với d.
Giải
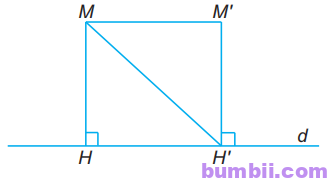
Kẻ MH và M’H’ vuông góc với đường thẳng d.
Do MH \(\bot\) d và M’H’ \(\bot\) d suy ra MH // M’H’.
Xét hai tam giác MHH’ và H’M’M có:
MH’ là cạnh chung;
\(\widehat{HMH’} =\widehat{M’H’M}\) (so le trong);
MH = H’M’ (theo giả thiết);
Do đó \(∆MHH’ = ∆H’M’M\) (c.g.c).
Suy ra \(\widehat{MH’H} =\widehat{H’MM’}\).
Hai góc trên ở vị trí so le trong nên MM’ // d.
\(\)
9.7. Dùng thước hai lề ta có thể dựng cặp đường thẳng song song với khoảng cách h không đổi.
Cho góc xOy. Dùng thước hai lề dựng cặp đường thẳng song song gồm đường thẳng chứa tia Ox và đường thẳng x’ (sao cho x’ cắt Oy) rồi dùng thước đo hai lề đó, dựng cặp đường thẳng song song gồm đường thẳng chứa tia Oy và đường thẳng y’ (sao cho y’ cắt Ox). Hai đường thẳng x’ và y’ cắt nhau tại P. Chứng minh rằng tia OP là tia phân giác của góc xOy.
Giải
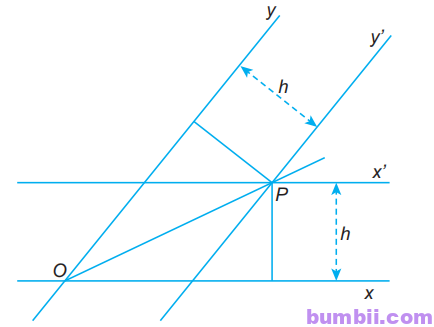
Do P thuộc đường thẳng x’ nên khoảng cách từ P đến x bằng h (vì x // x’)
Do P thuộc đường thẳng y’ nên khoảng cách từ P đến y bằng h (vì y // y’)
Suy ra P cách đều hai hai đường thẳng Ox và Oy.
Theo cách dựng, P nằm trong góc xOy.
Vậy P nằm trên đường phân giác của góc xOy.
\(\)
9.8. Cho tam giác ABC cân tại A. Chứng minh rằng khoảng cách từ B đến đường thẳng AC bằng khoảng cách từ C đến đường thẳng AB.
Giải
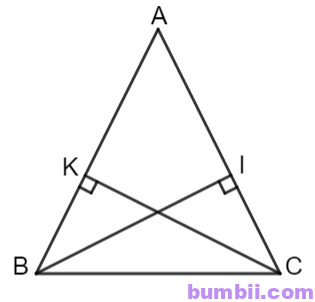
Kẻ BI \(\bot\) AC và CK \(\bot\) AB.
Xét hai tam giác vuông BCK và CBI có:
\(\widehat{B}=\widehat{C}\) (Do \(∆ABC\) cân tại A);
BC là cạnh huyền chung.
Do đó \(∆ADB = ∆AEC\) (cạnh huyền – góc nhọn)
Suy ra BI = CK (hai cạnh tương ứng).
\(\)
9.9. Cho tam giác ABC cân tại A và một điểm M tùy ý thuộc đoạn thẳng BC, M khác B và C. Chứng minh rằng tổng khoảng cách từ điểm M đến các đường thẳng AB, AC là một số không đổi.
Giải
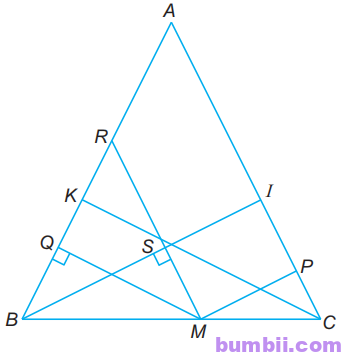
Gọi BI và CK là đường cao kẻ từ B và C của \(∆ABC.\)
Gọi MQ, MP lần lượt là khoảng cách từ M đến AB và AC.
Kẻ MR song song với cạnh AC (R ∈ AB).
MR giao với BI tại điểm S.
Tương tự cách làm của Bài 9.8 trong tam giác ABC cân tại A thì khoảng cách từ B đến AC bằng khoảng cách từ C đến AB. Ta suy ra được: BI = CK (1)
Tổng khoảng cách từ M đến AB và AC là MQ + MP (2)
Ta có: BI và MP cùng vuông góc với AC nên suy ra MP // BI hay MP // SI
Lại có: MR // AC hay MS // PI.
Suy ra MSIP là hình chữ nhật.
Do đó MP = SI (3)
Tam giác RBM cân tại R (do hai góc B và M bằng nhau). Với MQ là khoảng cách từ M đến RB và BS là khoảng cách từ điểm B đến RM. Chứng minh tương tự Bài 9.8, ta dễ dàng suy ra được MQ = BS (4)
Từ (1), (2), (3), (4) nên suy ra: MQ + MP = BS + SI = BI = CK.
Vậy tổng khoảng cách từ M đến AB và AC chinh bằng khoảng cách từ C đến AB nên không đổi.
\(\)
Xem bài giải trước: Bài 31: Quan hệ giữa góc và cạnh đối diện trong một tam giác
Xem bài giải tiếp theo: Bài 33: Quan hệ giữa ba cạnh của một tam giác
Xem thêm các bài giải khác tại: Giải Bài tập Toán Lớp 7 – NXB Kết Nối Tri Thức Với Cuộc Sống
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech
