Bài \(5\). Góc giữa đường thẳng và mặt phẳng. Góc nhị diện trang \(82\) Sách giáo khoa Toán lớp \(11\) tập \(2\) Chân trời sáng tạo. Các em cùng Bumbii giải các bài tập sau:
Bài \(1\). Cho tứ diện đều \(ABCD\). Vẽ hình bình hành \(BCED\).
\(a)\) Tìm góc giữa đường thẳng \(AB\) và \((BCD)\).
\(b)\) Tìm góc phẳng nhị diện \([A, CD, B]; [A, CD, E]\).
Trả lời:

\(a)\) Giả sử tứ diện đều có tất cả các cạnh bằng \(a\).
Gọi \(I\) là trung điểm của \(CD\), \(O\) là tâm của tam giác \(BCD\).
\(\Rightarrow AO \perp (BCD)\)
\(\Rightarrow (AB, (BCD)) = (AB, OB) = \widehat{ABO}\)
Tam giác \(BCD\) đều có trung tuyến \(BI\) nên ta có:
\(BI = \displaystyle \frac{a\sqrt{3}}{2}\)
\(\Rightarrow BO = \displaystyle \frac{2}{3}. \displaystyle \frac{a\sqrt{3}}{2} = \displaystyle \frac{a\sqrt{3}}{3}\)
Xét tam giác \(AOB\) vuông tại \(O\) nên ta có:
\(\cos{\widehat{ABO}} = \displaystyle \frac{BO}{AB} = \displaystyle \frac{\sqrt{3}}{3}\)
\(\Rightarrow \widehat{ABO} \approx 54,7^o\)
\(b)\) Tam giác \(ACD\) đều nên \(AI \perp CD\)
Tam giác \(BCD\) đều nên \(BI \perp CD\)
\(\Rightarrow \widehat{AIB}\) là góc phẳng nhị diện \([A, CD, B]\)
Ta có: \(OI = \displaystyle \frac{1}{3} BI = \displaystyle \frac{a\sqrt{3}}{6}\)
\(AO = \sqrt{AB^2 \ – \ BO^2} = \sqrt{a^2 \ – \ \left(\displaystyle \frac{a\sqrt{3}}{3}\right)^2} = \displaystyle \frac{a\sqrt{6}}{3}\)
Xét tam giác \(ABI\) có:
\(\tan{\widehat{AIB}} = \displaystyle \frac{AO}{OI} = 2\sqrt{2}\)
\(\Rightarrow \widehat{AIB} \approx 70,5^o\)
Tương tự có tam giác \(ACD, ECD\) đều nên \(AI \perp CD, EI \perp CD\)
Vậy \(\widehat{AIE}\) là góc phẳng nhị diện \([A, CD, E]\)
\(\Rightarrow \widehat{AIE} = 180^o \ – \ \widehat{AIB} = 109,5^o\)
\(\)
Bài \(2\). Cho hình chóp tứ giác đều \(S.ABCD\) có \(O\) là tâm của đáy và có tất cả các cạnh bằng nhau.
\(a)\) Tìm góc giữa đường thẳng \(SA\) và \((ABCD)\).
\(b)\) Tìm góc phẳng nhị diện \([A, SO, B], [S, AB, O]\).
Trả lời:

\(a)\) \(S.ABCD\) là chóp tứ giác đều với \(O\) là tâm của đáy nên \(SO \perp (ABCD)\)
\(\Rightarrow (SA, (ABCD)) = (SA, OA) = \widehat{SAO}\)
Giả sử chóp tứ giác đều có tất cả các cạnh bằng \(a\). Khi đó ta có:
\(AC = \sqrt{AB^2 + BC^2} = a\sqrt{2}\)
\(\Rightarrow AO = \displaystyle \frac{1}{2} AC = \displaystyle \frac{a\sqrt{2}}{2}\)
Xét tam giác \(SAO\) vuông tại \(O\) ta có:
\(\cos{\widehat{SAO}} = \displaystyle \frac{AO}{SA} = \displaystyle \frac{\frac{a\sqrt{2}}{2}}{a} = \displaystyle \frac{\sqrt{2}}{2}\)
\(\Rightarrow \widehat{SAO} = 45^o\)
Vậy \((SA, (ABCD)) = 45^o\)
\(b)\) Gọi \(I\) là trung điểm \(AB\)
Có \(SO \perp (ABCD) \Rightarrow SO \perp AO, SO \perp BO\)
Vậy \(\widehat{AOB}\) là góc phẳng nhị diện \([A, SO, B]\)
Do \(ABCD\) là hình vuông nên \(AC \perp BD\) hay \(\widehat{AOB} = 90^o\)
Lại có: Tam giác \(SAB\) đều nên \(SI \perp AB\).
Mà tam giác \(OAB\) vuông cân tại \(O\) nên \(OI \perp AB\)
Suy ra \(\widehat{SIO}\) là góc phẳng nhị diện \([S, AB, O]\).
Xét tam giác \(ABD\) có \(OI\) là đường trung bình nên \(OI = \displaystyle \frac{1}{2} AD = \displaystyle \frac{a}{2}\)
\(SO = \sqrt{SA^2 \ – \ AO^2} = \sqrt{a^2 \ – \ \left(\frac{a\sqrt{2}}{2}\right)^2} = \displaystyle \frac{a\sqrt{2}}{2}\)
Xét tam giác \(SOI\) vuông tại \(O\) ta có:
\(\tan{\widehat{SIO}} = \displaystyle \frac{SO}{OI} = \sqrt{2}\)
\(\Rightarrow \widehat{SIO} \approx 54,7^o\)
\(\)
Bài \(3\). Cho hình chóp cụt lục giác đều \(ABCDEF.A’B’C’D’E’F’\) với \(O\) và \(O’\) là tâm hai đáy, cạnh đáy lớn và đáy nhỏ lần lượt là \(a\) và \(\displaystyle \frac{a}{2}, OO’ = a\).
\(a)\) Tìm góc giữa cạnh bên và mặt đáy.
\(b)\) Tìm góc phẳng nhị diện \([O, AB, A’], [O’, A’B’, A]\).
Trả lời:

Kẻ \(C’H \perp OC (H \in OC\)
Khi đó \(OHC’O’\) là hình chữ nhật \(\Rightarrow C’H // OO’\)
Mà \(OO’ \perp (ABCDEF) \Rightarrow C’H \perp (ABCDEF)\)
\(\Rightarrow (CC’, (ABCDEF)) = (CC’, CH) = \widehat{HCC’}\)
Có \(HC = OC \ – \ OH = OC \ – \ O’C’ = \displaystyle \frac{a}{2}\)
\(C’H = OO’ = a\)
\(\Rightarrow \tan{\widehat{HCC’}} = \displaystyle \frac{C’H}{HC} = \displaystyle \frac{a}{\frac{a}{2}} = 2\)
\(\Rightarrow \widehat{HCC’} \approx 63,4^o\)
Vậy \((CC’, (ABCDEF)) = 63,4^o\)
\(b)\) Gọi \(M, M’\) lần lượt là trung điểm của \(AB, A’B’\)
\(\Rightarrow OM \perp AB, O’M’ \perp A’B’\)
Do \(ABB’A’\) là hình thang cân nên \(MM’ \perp AB, MM’ \perp A’B’\)
\(\Rightarrow [O, AB, A’] = \widehat{OMM’}, [O’, A’B’, A] = \widehat{MM’O’}\)
Kẻ \(M’K \perp OM (K \in OM)\)
Tứ giác \(OO’M’K\) là hình chữ nhật
\(\Rightarrow OK = O’M’ = \displaystyle \frac{A’B’ \sqrt{3}}{2} = \displaystyle \frac{a\sqrt{3}}{4}\)
\(OO’ = M’K = a\)
Có \(OM = \displaystyle \frac{AB \sqrt{3}}{2} = \displaystyle \frac{a\sqrt{3}}{2}\)
\(\Rightarrow MK = OM \ – \ OK = \displaystyle \frac{a\sqrt{3}}{2} \ – \ \displaystyle \frac{a\sqrt{3}}{4} = \displaystyle \frac{a\sqrt{3}}{4}\)
Xét tam giác \(MKM’\) vuông tại \(K\) nên ta có:
\(\tan{\widehat{OMM’}} = \displaystyle \frac{M’K}{MK} = \displaystyle \frac{4}{\sqrt{3}}\)
\(\Rightarrow \widehat{OMM’} \approx 66,6^o\)
\(\Rightarrow \widehat{MM’O’} \approx 180^o \ – \ \widehat{OMM’} = 113,4^o\)
\(\)
Bài \(4\). Một con dốc có dạng hình lăng trụ đứng tam giác với kích thước như trong Hình \(9\).
\(a)\) Tính số đo góc giữa đường thẳng \(CA’\) và \((CC’B’B)\).
\(b)\) Tính số đo góc nhị diện cạnh \(CC’\)
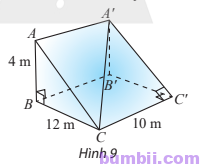
Trả lời:
\(a)\) Ta có \(BB’ \perp (A’B’C’) \Rightarrow BB’ \perp A’B’\)
Lại có \(A’B’ \perp B’C’\)
\(\Rightarrow A’B’ \perp (CC’B’B)\)
\(\Rightarrow (CA’, (CC’B’B)) = (CA’, CB’) = \widehat{A’CB’}\)
Xét tam giác \(CBB’\) vuông tại \(B\) ta có:
\(B’C = \sqrt{BB’^2 + BC^2} = \sqrt{10^2 + 12^2} = 2\sqrt{61}\)
Có \(A’B’ = AB = 4\)
\(\Rightarrow \tan{\widehat{A’CB’}} = \displaystyle \frac{A’B’}{B’C} = \displaystyle \frac{2}{\sqrt{61}}\)
\(\Rightarrow \widehat{A’CB’} \approx 14,4^o\)
Vậy \((CA’, (CC’B’B)) = 14,4^o\)
\(b)\) Có \(CC’ \perp (ABC) \Rightarrow CC’ \perp AC, CC’ \perp BC\)
Vậy \(\widehat{ACB}\) là góc nhị diện cạnh \(CC’\)
\(\tan{\widehat{ACB}} = \displaystyle \frac{AB}{BC} = \displaystyle \frac{1}{3}\)
\(\Rightarrow \widehat{ACB} \approx 18,4^o\)
\(\)
Bài \(5\). Người ta định đào một cái hầm có dạng hình chóp cụt tứ giác đều có hai cạnh đáy là \(14\) m và \(10\) m. Mặt bên tạo với đáy nhỏ thành một góc nhị diện có số đo bằng \(135^o\). Tính số mét khối đất cần phải di chuyển ra khỏi hầm.
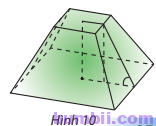
Trả lời:

Mô hình hoá cái hầm bằng chóp cụt tứ giác đều \(ABCD.A’B’C’D’\) với \(O, O’\) là tâm hai đáy.
Vậy \(AB = 14, A’B’ = 10\)
Gọi \(M, M’\) lần lượt là trung điểm của \(CD, C’D’\).
\(A’B’C’D’\) là hình vuông nên \(O’M’ \perp C’D’\)
\(CDD’C’\) là hình thang cân nên \(MM’ \perp C’D’\)
Vậy \(\widehat{MM’O’}\) là góc nhị diện giữa mặt bên và đáy nhỏ.
\(\Rightarrow \widehat{MM’O’} = 135^o\)
\(\Rightarrow \widehat{M’MO} = 180^o \ – \ \widehat{MM’O} = 45^o\)
Kẻ \(M’H \perp OM (H \in OM)\).
Tứ giác \(OHM’O’\) là hình chữ nhật nên \(OH = O’M’ = 5\)
\(MH = OM \ – \ OH = \displaystyle \frac{14}{2} \ – \ \displaystyle \frac{10}{2} = 2\)
\(M’H = OO’ = MH. \tan{45^o} = 2\)
Diện tích đáy lớn là:
\(S = AB^2 = 14^2 = 196 (m^2)\)
Diện tích đáy nhỏ là:
\(S’ = A’B’^2 = 10^2 = 100 (m^2)\)
Số mét khối đất cần phải di chuyển ra khỏi hầm (thể tích của hình chóp cụt tứ giác đều) là:
\(V = \displaystyle \frac{1}{3}. h. (S + \sqrt{S. S’} + S’)\)
\(= \displaystyle \frac{1}{2}. 2. (196 + \sqrt{196. 100} + 100) \approx 290,67 (m^3)\)
Bài 5. Góc giữa đường thẳng Bài 5. Góc giữa đường thẳng Bài 5. Góc giữa đường thẳng Bài 5. Góc giữa đường thẳng
Xem bài giải trước: Bài 4 – Khoảng cách trong không gian
Xem bài giải tiếp theo: Bài tập cuối chương VIII
Xem các bài giải khác: Giải bài tập SGK Toán Lớp 11 Chân trời sáng tạo
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech

Hạnh phúc đạt được khi bạn ngừng chờ đợi điều đó xảy ra và thực hiện các bước để biến nó thành hiện thực.