Bài 4: Thứ tự thực hiện phép tính. Quy tắc dấu ngoặc

Chương 1 – Bài 4: Thứ tự thực hiện phép tính. Quy tắc dấu ngoặc trang 21 sách bài tập toán lớp 7 tập 1 NXB Cánh Diều. Các em cùng Bumbii giải các bài tập sau.

31. Tính giá trị của mỗi biểu thức sau:

a) \(12.\left(\displaystyle\frac{2}{3}-\displaystyle\frac{5}{6}\right)^2;\)

b) \(4.\left(-\displaystyle\frac{1}{3}\right)^3-2.\left(-\displaystyle\frac{1}{3}\right)^2+3.\left(-\displaystyle\frac{1}{3}\right)+1.\)

Giải

a) \(12.\left(\displaystyle\frac{2}{3}-\displaystyle\frac{5}{6}\right)^2=12.\left(\displaystyle\frac{4}{6}-\displaystyle\frac{5}{6}\right)^2\)

\(=12.\left(\displaystyle\frac{-1}{6}\right)^2=12.\displaystyle\frac{1}{36}=\displaystyle\frac{1}{3}.\)

b) \(4.\left(-\displaystyle\frac{1}{3}\right)^3-2.\left(-\displaystyle\frac{1}{3}\right)^2+3.\left(-\displaystyle\frac{1}{3}\right)+1\)

\(=4.\displaystyle\frac{-1}{8}-2.\displaystyle\frac{1}{4}+\displaystyle\frac{-3}{2}+1\)

\(=\displaystyle\frac{-1}{2}-\displaystyle\frac{1}{2}+\displaystyle\frac{-3}{2}+\displaystyle\frac{2}{2}=\displaystyle\frac{-3}{2}.\)

\(\)

31. Tính giá trị của mỗi biểu thức sau:

a) \(\displaystyle\frac{45}{4}-\left(2\displaystyle\frac{5}{7}+5,25\right);\)

b) \(\displaystyle\frac{5}{9}:2,4-\displaystyle\frac{41}{9}:2,4;\)

c) \(\left(-\displaystyle\frac{3}{4}+\displaystyle\frac{5}{13}\right).\displaystyle\frac{7}{2}-\left(\displaystyle\frac{9}{4}-\displaystyle\frac{8}{13}\right).\displaystyle\frac{7}{2}.\)

Giải

a) \(\displaystyle\frac{45}{4}-\left(2\displaystyle\frac{5}{7}+5,25\right)=\displaystyle\frac{45}{4}-\left(\displaystyle\frac{19}{7}+\displaystyle\frac{21}{4}\right)\)

\(=\displaystyle\frac{45}{4}-\displaystyle\frac{19}{7}-\displaystyle\frac{21}{4}=\displaystyle\frac{45}{4}-\displaystyle\frac{21}{4}-\displaystyle\frac{19}{7}\)

\(=6-\displaystyle\frac{19}{7}=\displaystyle\frac{42}{7}-\displaystyle\frac{19}{7}=\displaystyle\frac{23}{7}.\)

b) \(\displaystyle\frac{5}{9}:2,4-\displaystyle\frac{41}{9}:2,4=\displaystyle\frac{5}{9}:\displaystyle\frac{12}{5}-\displaystyle\frac{41}{9}:\displaystyle\frac{12}{5}\)

\(=\displaystyle\frac{5}{9}.\displaystyle\frac{5}{12}-\displaystyle\frac{41}{9}.\displaystyle\frac{5}{12}=\displaystyle\frac{5}{12}.\left(\displaystyle\frac{5}{9}-\displaystyle\frac{41}{9}\right)\)

\(=-4.\displaystyle\frac{5}{12}=\displaystyle\frac{-5}{3}.\)

c) \(\left(-\displaystyle\frac{3}{4}+\displaystyle\frac{5}{13}\right).\displaystyle\frac{7}{2}-\left(\displaystyle\frac{9}{4}-\displaystyle\frac{8}{13}\right).\displaystyle\frac{7}{2}\)

\(=\left[\left(-\displaystyle\frac{3}{4}+\displaystyle\frac{5}{13}\right)-\left(\displaystyle\frac{9}{4}-\displaystyle\frac{8}{13}\right)\right].\displaystyle\frac{7}{2}\)

\(=\left(-\displaystyle\frac{3}{4}+\displaystyle\frac{5}{13}-\displaystyle\frac{9}{4}+\displaystyle\frac{8}{13}\right).\displaystyle\frac{7}{2}\)

\(=\left[\left(-\displaystyle\frac{3}{4}-\displaystyle\frac{9}{4}\right)+\left(\displaystyle\frac{8}{13}+\displaystyle\frac{5}{13}\right)\right].\displaystyle\frac{7}{2}\)

\(=(-3+1).\displaystyle\frac{7}{2}=(-2).\displaystyle\frac{7}{2}=-7.\)

\(\)

32. Cho \(A=\displaystyle\frac{13}{50}.(-15,5)-\displaystyle\frac{13}{50}.84\displaystyle\frac{1}{2};\) \(B=\displaystyle\frac{(-0,7)^2.(-0,5)^3}{\left(-\displaystyle\frac{7}{3}\right)^3.\left(\displaystyle\frac{3}{2}\right)^4.(-1)^5}.\)

Bạn An tính được giá trị của các biểu thức trên \(A =-26;\ B=\displaystyle\frac{-20}{21}.\) Theo em, bạn An tính đúng hay sai?

Giải

\(A=\displaystyle\frac{13}{50}.(-15,5)-\displaystyle\frac{13}{50}.84\displaystyle\frac{1}{2}\)

\(=\displaystyle\frac{13}{50}.(-15,5)-\displaystyle\frac{13}{50}.84,5\)

\(=\displaystyle\frac{13}{50}.(-15,5-84,5)\)

\(=\displaystyle\frac{13}{50}.(-100)=-26.\)

\(B=\displaystyle\frac{(-0,7)^2.(-0,5)^3}{\left(-\displaystyle\frac{7}{3}\right)^3.\left(\displaystyle\frac{3}{2}\right)^4.(-1)^5}\)

\(=\displaystyle\frac{0,49.(-125)}{\left(-\displaystyle\frac{343}{27}\right).\displaystyle\frac{81}{16}.(-1)}=\displaystyle\frac{-61,25}{\displaystyle\frac{1029}{16}}\)

\(=-61,25:\displaystyle\frac{1029}{16}=\displaystyle\frac{-245}{4}.\displaystyle\frac{16}{1029}=\displaystyle\frac{-20}{21}.\)

Như vậy, bạn An đã tính đúng.

\(\)

33. Cho \(A=\displaystyle\frac{\displaystyle\frac{-1}{2}-5.\left(\displaystyle\frac{3}{2}\right)^2}{15\displaystyle\frac{2}{9}+\left(-\displaystyle\frac{2}{3}\right)^2};\) \(B=\displaystyle\frac{7}{12}.3,4-\displaystyle\frac{7}{12}.8,8.\)

Tính \(A-5B.\)

Giải

Ta có: \(A=\displaystyle\frac{\displaystyle\frac{-1}{2}-5.\left(\displaystyle\frac{3}{2}\right)^2}{15\displaystyle\frac{2}{9}+\left(-\displaystyle\frac{2}{3}\right)^2}=\displaystyle\frac{\displaystyle\frac{-1}{2}-5.\displaystyle\frac{9}{4}}{\displaystyle\frac{137}{9}+\displaystyle\frac{4}{9}}\)

\(=\displaystyle\frac{\displaystyle\frac{-1}{2}-\displaystyle\frac{45}{4}}{\displaystyle\frac{47}{3}}=\displaystyle\frac{\displaystyle\frac{-47}{4}}{\displaystyle\frac{47}{3}}=\displaystyle\frac{-47}{4}:\displaystyle\frac{47}{3}\)

\(=\displaystyle\frac{-47}{4}.\displaystyle\frac{3}{47}=\displaystyle\frac{-3}{4}.\)

\(B=\displaystyle\frac{7}{12}.3,4-\displaystyle\frac{7}{12}.8,8=\displaystyle\frac{7}{12}.(3,4-8,8)\)

\(=\displaystyle\frac{7}{12}.(-5,4)=\displaystyle\frac{7}{12}.\displaystyle\frac{-27}{5}=\displaystyle\frac{-63}{20}.\)

Do đó \(A-5B=\displaystyle\frac{-3}{4}-5.\displaystyle\frac{-63}{20}\) \(=\displaystyle\frac{-3}{4}-\displaystyle\frac{-63}{4}=15.\)

\(\)

34. Chọn dấu “<“, “>”, “=” thích hợp cho \(\fbox{?}:\)

a) \(\displaystyle\frac{5}{6}-\left(\displaystyle\frac{1}{6}\right)^2\ \fbox{ ? }\ \left(\displaystyle\frac{5}{6}-\displaystyle\frac{1}{6}\right)^2;\)

b) \(250.\left(\displaystyle\frac{1}{5}-\displaystyle\frac{1}{6}\right)^2\ \fbox{ ? }\ 250.\left(\displaystyle\frac{1}{5}\right)^2-\displaystyle\frac{1}{6};\)

c) \(3\displaystyle\frac{1}{5}:1,5+4\displaystyle\frac{2}{5}:1,5\ \fbox{ ? }\ \left(3\displaystyle\frac{1}{5}+4\displaystyle\frac{2}{5}\right):1,5;\)

d) \(\left(\displaystyle\frac{9}{25}-2,18\right):\left(3\displaystyle\frac{4}{5}+0,2\right)\ \fbox{ ? }\ \displaystyle\frac{9}{25}:3\displaystyle\frac{4}{5}-2,18:0,2.\)

Giải

a) Ta có:

\(\displaystyle\frac{5}{6}-\left(\displaystyle\frac{1}{6}\right)^2=\displaystyle\frac{5}{6}-\displaystyle\frac{1}{36}=\displaystyle\frac{30}{36}-\displaystyle\frac{1}{36}=\displaystyle\frac{29}{36};\)

\(\left(\displaystyle\frac{5}{6}-\displaystyle\frac{1}{6}\right)^2=\left(\displaystyle\frac{2}{3}\right)^2=\displaystyle\frac{4}{9}=\displaystyle\frac{16}{36}.\)

Vì \(\displaystyle\frac{29}{36}>\displaystyle\frac{16}{36}\) nên \(\displaystyle\frac{5}{6}-\left(\displaystyle\frac{1}{6}\right)^2\ \fbox{>}\ \left(\displaystyle\frac{5}{6}-\displaystyle\frac{1}{6}\right)^2\)

b) Ta có:

\(250.\left(\displaystyle\frac{1}{5}-\displaystyle\frac{1}{6}\right)^2=250.\left(\displaystyle\frac{6}{30}-\displaystyle\frac{5}{30}\right)^2\)

\(=250.\left(\displaystyle\frac{1}{30}\right)^2=250.\displaystyle\frac{1}{900}=\displaystyle\frac{5}{18};\)

\(250.\left(\displaystyle\frac{1}{5}\right)^2-\displaystyle\frac{1}{6}=250.\displaystyle\frac{1}{25}-\displaystyle\frac{1}{6}\)

\(=10-\displaystyle\frac{1}{6}=\displaystyle\frac{60}{6}-\displaystyle\frac{1}{6}=\displaystyle\frac{59}{6}=\displaystyle\frac{177}{18}.\)

Vì \(\displaystyle\frac{5}{18}<\displaystyle\frac{177}{18}\) nên \(250.\left(\displaystyle\frac{1}{5}-\displaystyle\frac{1}{6}\right)^2\ \fbox{<}\ 250.\left(\displaystyle\frac{1}{5}\right)^2-\displaystyle\frac{1}{6}.\)

c) Ta có: \(3\displaystyle\frac{1}{5}:1,5+4\displaystyle\frac{2}{5}:1,5= \left(3\displaystyle\frac{1}{5}+4\displaystyle\frac{2}{5}\right):1,5;\)

\(3\displaystyle\frac{1}{5}:1,5+4\displaystyle\frac{2}{5}:1,5\ \fbox{=}\ \left(3\displaystyle\frac{1}{5}+4\displaystyle\frac{2}{5}\right):1,5.\)

d) Ta có:

\(\left(\displaystyle\frac{9}{25}-2,18\right):\left(3\displaystyle\frac{4}{5}+0,2\right)\)

\(=\left(\displaystyle\frac{9}{25}-\displaystyle\frac{109}{50}\right):\left(\displaystyle\frac{19}{5}+\displaystyle\frac{1}{5}\right)\)

\(=\displaystyle\frac{-91}{50}:\displaystyle\frac{40}{10}=\displaystyle\frac{-91}{50}:\displaystyle\frac{10}{40}=\displaystyle\frac{-91}{200};\)

\(\displaystyle\frac{9}{25}:3\displaystyle\frac{4}{5}-2,18:0,2\)

\(=\displaystyle\frac{9}{25}:\displaystyle\frac{19}{5}-\displaystyle\frac{109}{50}:\displaystyle\frac{1}{5}\)

\(=\displaystyle\frac{9}{25}.\displaystyle\frac{5}{19}-\displaystyle\frac{109}{50}.5\)

\(=\displaystyle\frac{9}{95}-\displaystyle\frac{109}{10}=\displaystyle\frac{-2053}{190}.\)

Vì \(\displaystyle\frac{-91}{200}>-1;\ \displaystyle\frac{-2053}{190}<-1\)

Vậy \(\left(\displaystyle\frac{9}{25}-2,18\right):\left(3\displaystyle\frac{4}{5}+0,2\right)\ \fbox{>}\ \displaystyle\frac{9}{25}:3\displaystyle\frac{4}{5}-2,18:0,2.\)

\(\)

35. Cho \(A=\left(17,81:1,37-\displaystyle\frac{59}{3}:\displaystyle\frac{11}{6}\right)+\displaystyle\frac{(0,8)^3}{(0,4)^3.11}.\)

Chứng minh rằng \(A+1\) là bình phương của một số tự nhiên.

Giải

\(A=\left(17,81:1,37-\displaystyle\frac{59}{3}:\displaystyle\frac{11}{6}\right)+\displaystyle\frac{(0,8)^3}{(0,4)^3.11}\)

\(=\left(13-\displaystyle\frac{59}{3}.\displaystyle\frac{6}{11}\right)+\displaystyle\frac{0,512}{0,064.11}\)

\(=\left(13-\displaystyle\frac{118}{11}\right)+\displaystyle\frac{8}{11}=\displaystyle\frac{25}{11}+\displaystyle\frac{8}{11}=3.\)

Suy ra \(A+1=3+1=4=2^2.\)

Vậy \(A+1\) là bình phương của số tự nhiên 2.

\(\)

36. Một vườn trường có dạng hình chữ nhật với độ dài hai cạnh là 26 m và 14 m. Người ta muốn rào xung quanh vườn, cứ cách 2 m đóng một cọc rào, mỗi góc vườn đều đóng một cọc rào và chỉ để một cửa ra vào vườn rộng 4 m. Tính số cọc rào cần dùng, biết rằng hai cạnh bên của cửa đồng thời là hai cọc rào.

Giải

Chu vi của vườn trường là:

\((26 + 14) . 2 = 80\) (m).

Chiều dài của hàng rào là:

\(80-4 = 76\) (m).

Số cọc rào cần dùng là:

\(76 : 2 + 1 = 39\) (cọc).

\(\)

37. Quan sát biển báo giao thông ở Hình 7.

a) Tính diện tích của biển báo, biết rằng đường kính của biển báo là 87,5 cm (lấy π = 3,14).

b) Ở chính giữa của biển báo là hình chữ nhật được sơn màu trắng có chiều dài là 70,3 cm và chiều rộng là 12,3 cm. Phần còn lại của biển báo được sơn màu đỏ. Tính diện tích phần được sơn màu đỏ của biển báo.

Giải

a) Bán kính của biển báo là:

\(87,5 : 2 = 43,75\ (cm).\)

Diện tích của biển báo là:

\(43,75 . 43,75 . 3,14 = 6\ 010,15625\ (cm^2).\)

b) Diện tích hình chữ nhật được sơn mày trắng của biển báo là:

\(70,3 . 12,3 = 864,69\ (cm^2).\)

Diện tích phần được sơn mày đỏ của biển báo là:

\(6\ 010,15625-864,69 = 5 145,46625\ (cm^2).\)

\(\)

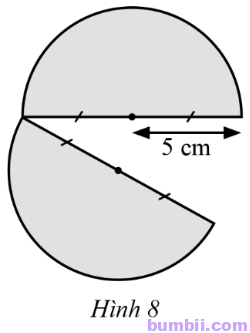
38. Người ta cắt một tấm tôn có dạng hình tròn bán kính 5 cm thành hai phần bằng nhau như Hình 8. Tính chu vi của tấm tôn sau khi bị cắt (lấy π = 3,14).