Chương 3 – Bài 4. Đồ thị của hàm số bậc nhất y = ax + b (a ≠ 0) trang 77 sách giáo khoa toán lớp 8 tập 1 Cánh Diều. Các em cùng Bumbii giải các bài tập sau.
1. Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai về đường thẳng d là đồ thị của hàm số y = ax + b (a ≠ 0)?
a) Đường thẳng d cắt trục tung tại điểm có tung độ bằng \(-\displaystyle\frac{b}{a}.\)
b) Đường thẳng d cắt trục hoành tại điểm có hoành độ bằng b
c) Đường thẳng d cắt trục tung tại điểm có tung độ bằng b.
d) Đường thẳng d cắt trục hoành tại điểm có hoành độ bằng \(-\displaystyle\frac{b}{a}.\)
Giải
Đường thẳng d cắt trục tung nên \(y = 0\) nên ta có \(ax + b = 0.\)
Suy ra \(ax =-b\) nên \(x=-\displaystyle\frac{b}{a}.\)
Do đó, phát biểu a) đúng, phát biểu c) sai.
Đường thẳng d cắt trục hoành nên \(x = 0\) nên ta có \(y = a . 0 + b = 0 + b = b.\)
Do đó, phát biểu b) đúng, phát biểu d) sai.
\(\)
2. Chỉ ra các cặp đường thẳng cắt nhau và các cặp đường thẳng song song trong số các đường thẳng sau: \(y =-2x + 5;\ y =-2x;\ y = 4x-1.\)
Giải
Hai đường thẳng \(y = -2x + 5;\) \(y = -2x\) có hệ số góc bằng nhau và hệ số tự do khác nhau nên hai đường thẳng này song song.
Hai đường thẳng \(y = -2x + 5;\) \(y = 4x-1\) có hệ số góc khác nhau nên hai đường thẳng này cắt nhau.
Hai đường thẳng \(y = -2x;\) \(y = 4x-1\) có hệ số góc khác nhau nên hai đường thẳng này cắt nhau.
\(\)
3. Vẽ đồ thị các hàm số: \(y = 3x;\) \(y = 3x + 4;\) \(y = -\displaystyle\frac{1}{2}x;\) \(y = -\displaystyle\frac{1}{2}x + 3\) trên cùng một mặt phẳng tọa độ.
Giải
• Hàm số \(y = 3x.\)
Với \(x=1\) thì \(y=3\) ta được điểm \(A(1;3)\) thuộc đồ thị của hàm số \(y = 3x.\)
Vậy đồ thị của hàm số \(y = 3x\) là đường thẳng đi qua hai điểm \(O(0;0)\) và \(A(1;3).\)
• Hàm số \(y = 3x + 4\)
Với \(x=0\) thì \(y=4\) ta được điểm \(B(0;4)\) thuộc đồ thị của hàm số \(y = 3x + 4.\)
Với \(y=0\) thì \(x=-\displaystyle\frac{4}{3}\) ta được điểm \(C\left(-\displaystyle\frac{4}{3};0\right)\) thuộc đồ thị của hàm số \(y = 3x + 4.\)
Vậy đồ thị của hàm số \(y = 3x + 4;\) là đường thẳng đi qua hai điểm \(B(0;4)\) và \(C\left(-\displaystyle\frac{4}{3};0\right).\)
• Hàm số \(y = -\displaystyle\frac{1}{2}x\)
Với \(x=2\) thì \(y=-1\) ta được điểm \(D(2;-1)\) thuộc đồ thị của hàm số \(y = -\displaystyle\frac{1}{2}x.\)
Vậy đồ thị của hàm số \(y = -\displaystyle\frac{1}{2}x\) là đường thẳng đi qua hai điểm \(O(0;0)\) và \(D(2;-1).\)
• Hàm số \(y = -\displaystyle\frac{1}{2}x + 3\)
Với \(x=0\) thì \(y=3\) ta được điểm \(E(0;3)\) thuộc đồ thị của hàm số \(y = -\displaystyle\frac{1}{2}x + 3.\)
Với \(y=0\) thì \(x=6\) ta được điểm \(F(6;0)\) thuộc đồ thị của hàm số \(y = -\displaystyle\frac{1}{2}x + 3\)
Vậy đồ thị của hàm số \(y = -\displaystyle\frac{1}{2}x + 3\) là đường thẳng đi qua hai điểm \(E(0;3)\) và \(F(6;0).\)
Vẽ đồ thị các hàm số trên cùng một mặt phẳng tọa độ như sau:
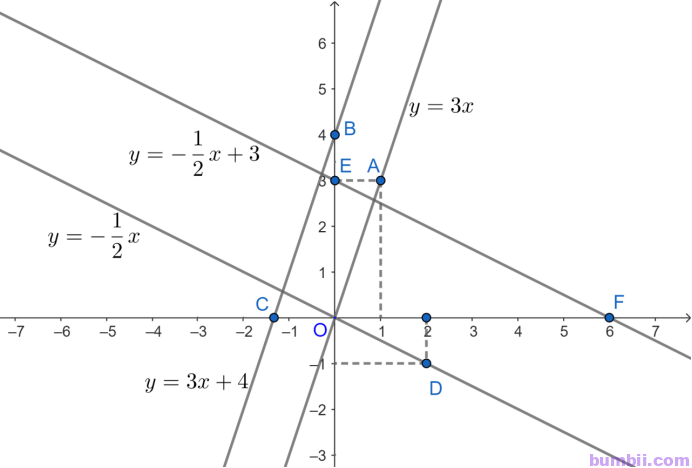
\(\)
4. Xác định đường thẳng y = ax + b (a ≠ 0) có hệ số góc bằng -1 và đi qua điểm M(1;2). Sau đó vẽ đường thẳng tìm được trên mặt phẳng toạ độ.
Giải
Vì đường thẳng đi qua điểm \(M(1;2)\) và có hệ số góc bằng \(-1\) nên ta có: \(2 = (-1).1+b\) suy ra \(b = 3.\)
Do đó đường thẳng có dạng \(y = -x + 3.\)
Với \(x = 0\) thì \(y = 3,\) ta được điểm \(A(0;3)\) thuộc đồ thị của hàm số \(y = -x + 3.\)
Với \(y = 0\) thì \(x = 3,\) ta được điểm \(B(3;0)\) thuộc đồ thị của hàm số \(y = -x + 3.\)
Vậy đồ thị của hàm số \(y = -x + 3\) là đường thẳng đi qua hai điểm \(A(0;3)\) và \(B(3;0).\)
Ta vẽ đồ thị hàm số như sau:
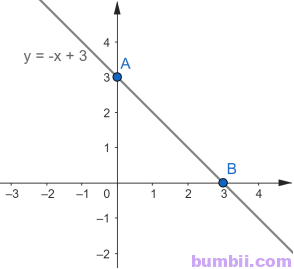
\(\)
5. a) Vẽ đường thẳng y = 2x – 1 trong mặt phẳng toạ độ.
b) Xác định đường thẳng y = ax + b (a ≠ 0) đi qua điểm M(1;3) và song song với đường thẳng y = 2x – 1. Sau đó vẽ đường thắng tìm được trên mặt phẳng toạ độ.
Giải
a) Đường thẳng \(y = 2x-1.\)
Với \(x = 0\) thì \(y =-1,\) ta được điểm \(A(0;-1)\) thuộc đồ thị của hàm số \(y = 2x-1.\)
Với \(y = 0\) thì \(x=\displaystyle\frac{1}{2},\) ta được điểm \(B\left(\displaystyle\frac{1}{2};0\right)\) thuộc đồ thị của hàm số \(y = 2x-1.\)
Vậy đồ thị của hàm số \(y = 2x-1\) là đường thẳng đi qua hai điểm \(A(0;-1)\) và \(B\left(\displaystyle\frac{1}{2};0\right).\)
Ta vẽ đồ thị hàm số \(y = 2x-1\) như sau:
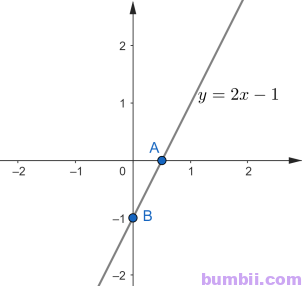
b) Đường thẳng \(y = ax + b\ (a ≠ 0)\) song song với đường thẳng \(y = 2x-1\) nên đường thẳng có dạng \(y = 2x + b.\)
Mặt khác, đường thẳng \(y = 2x + b\) đi qua điểm \(M(1;3)\) nên \(2 . 1 + b = 3\) suy ra \(b = 1.\)
Do đó, đường thẳng cần tìm là \(y = 2x + 1.\)
Với \(x = 0\) thì \(y = 1,\) ta được điểm \(C(0;1)\) thuộc đồ thị của hàm số \(y = 2x + 1.\)
Với \(y = 0\) thì \(x=-\displaystyle\frac{1}{2},\) ta được điểm \(D\left(-\displaystyle\frac{1}{2};0\right)\) thuộc đồ thị của hàm số \(y = 2x + 1.\)
Vậy đồ thị của hàm số \(y = 2x + 1\) là đường thẳng đi qua hai điểm \(C(0;1)\) và \(D\left(-\displaystyle\frac{1}{2};0\right).\)
Ta vẽ đồ thị hàm số \(y = 2x + 1\) như sau:
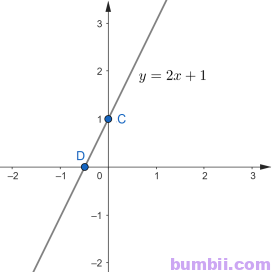
\(\)
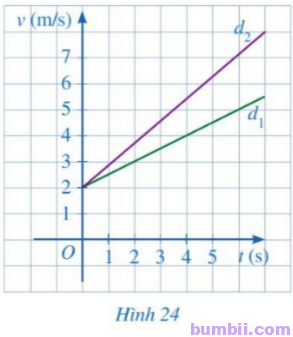
6. Một phân đường thẳng \(d_1;\ d_2\) ở Hình 24 lần lượt biểu thị tốc độ (đơn vị: m/s) của vật thứ nhất, vật thứ hai theo thời gian t(s).
a) Nêu nhận xét về tung độ giao điểm của hai đường thẳng \(d_1;\ d_2.\) Từ đó, nêu nhận xét về tốc độ ban đầu của hai chuyển động.
b) Trong hai đường thẳng \(d_1;\ d_2\) đường thẳng nào có hệ số góc lớn hơn?
c) Từ giây thứ nhất trở đi, vật nào có tốc độ lớn hơn? Vì sao?
Giải
a) Tung độ giao điểm của hai đường thẳng \(d_1,\ d_2\) tại điểm có tung độ bằng \(2.\)
Do đó, tốc độ ban đầu của hai chuyển động bằng nhau.
b) Trong hai đường thẳng \(d_1,\ d_2\), đường thẳng \(d_2\) có độ dốc lớn hơn nên có hệ số góc lớn hơn.
c) Khi lấy hai điểm bất kỳ có cùng hoành độ (với \(t>1\)) trên \(d_1\) và \(d_2\) thì tung độ của điểm trên \(d_2>d_1\) nên tốc độ vật thứ hai có tốc độ lớn hơn.
Vậy từ giây thứ nhất trở đi, vật thứ hai có tốc độ lớn hơn.
\(\)
Xem bài giải trước: Bài 3. Hàm số bậc nhất y = ax + b (a ≠ 0)
Xem bài giải tiếp theo: Bài tập cuối chương 3
Xem thêm các bài giải khác tại: Giải bài tập SGK Toán Lớp 8 Cánh Diều
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech
