Chương 4 – Bài 2: Tia phân giác của một góc trang 106 sách bài tập toán lớp 7 tập 1 NXB Cánh Diều. Các em cùng Bumbii giải các bài tập sau.
8. Ở Hình 16 có \(\widehat{xOz}=40^o,\ \widehat{xOy}=80^o.\) Tia \(Oz\) có là tia phân giác của góc \(xOy\) hay không?
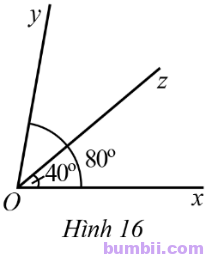
Giải
Do \(\widehat{xOz}\) và \(\widehat{yOz}\) là hai góc kề nhau nên \(\widehat{xOz}+\widehat{yOz}=\widehat{xOy}.\)
Suy ra \(\widehat{yOz}=\widehat{xOy}-\widehat{xOz}=80^o-40^o=40^o.\)
Nên \(\widehat{xOz}=\widehat{yOz}\) (cùng bằng \(40^o\)).
Mặt khác \(Oz\) nằm giữa hai tia \(Ox\) và \(Oy.\)
Do đó \(Oz\) là tia phân giác của góc \(xOy.\)
\(\)
9. Ở Hình 17 có On, Oq lần lượt là tia phân giác của góc mOp, pOr. Tính số đo mỗi góc mOr, pOq, mOn, nOq.
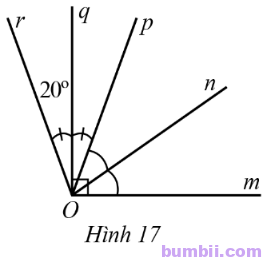
Giải
Do \(\widehat{mOq}\) và \(\widehat{qOr}\) là hai góc kề nhau nên:
\(\widehat{mOr}=\widehat{mOq}+\widehat{qOr}=90^o+20^o=110^o.\)
Do Oq là tia phân giác của \(\widehat{pOr}\) nên \(\widehat{pOq}=\widehat{qOr}=20^o.\)
Do \(\widehat{mOp}\) và \(\widehat{qOp}\) là hai góc kề nhau nên \(\widehat{mOp}+\widehat{pOq}=\widehat{mOq}.\)
Suy ra \(\widehat{mOp}=\widehat{mOq}-\widehat{pOq}=90^o-20^o=70^o.\)
Lại có On là tia phân giác của \(\widehat{mOp}\) nên \(\widehat{mOn}=\widehat{nOp}=70^o:2=35^o.\)
Do \(\widehat{nOp}\) và \(\widehat{pOq}\) là hai góc kề nhau nên:
\(\widehat{nOq}=\widehat{nOp}+\widehat{pOq}=35^o+20^o=55^o.\)
Vậy \(\widehat{mOr}=110^o,\ \widehat{pOq}=20^o,\) \(\widehat{mOn}=35^o,\) \(\widehat{nOq}=55^o.\)
\(\)
10. Ở Hình 18 có \(\widehat{xOM}=\widehat{yON}=30^o,\) OI là tia phân giác của góc MON. Hai đường thẳng OI, xy có vuông góc với nhau hay không?
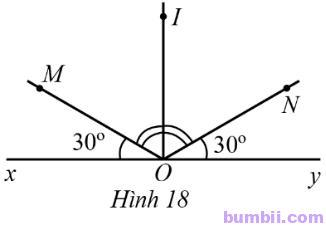
Giải
Ta có \(\widehat{MON}\) và \(\widehat{yON}\) là hai góc kề nhau nên \(\widehat{MOy}=\widehat{MON}+\widehat{yON}.\)
Mà \(\widehat{xOM} + \widehat{MOy}=180^o\) (hai góc kề bù)
Do đó \(\widehat{xOM}+\widehat{MON}+\widehat{yON}=180^o\)
Suy ra \(\widehat{MON}=180^o-\widehat{yON}-\widehat{xOM}\) \(=180^o-30^o-30^o=120^o.\)
Do \(OI\) là tia phân giác của \(\widehat{MON}\) nên
\(\widehat{MOI}=\widehat{ION}=\displaystyle\frac{1}{2}\widehat{MON}=\displaystyle\frac{1}{2}.120^o=60^o.\)
Lại có \(\widehat{xOM}\) và \(\widehat{MOI}\) là hai góc kề nhau nên \(\widehat{xOI}=\widehat{xOM}+\widehat{MOI}=30^o+60^o=90^o.\)
Do đó \(OI\) vuông góc với \(xy.\)
\(\)
11. Ở Hình 19 có \(\widehat{COD}=80^o,\ \widehat{COE}=60^o,\) tia OG là tia phân giác của góc COD.
a) Tính số đo góc EOG.
b) Tia OE có là tia phân giác của góc DOG hay không?
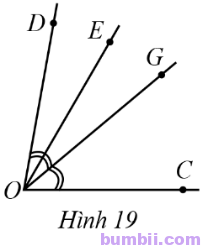
Giải
a) Do tia OG là tia phân giác của \(\widehat{COD}\) nên
\(\widehat{COG}=\widehat{GOD}=\displaystyle\frac{1}{2}\widehat{COD}=\displaystyle\frac{1}{2}.80^o=40^o.\)
Do \(\widehat{EOG}\) và \(\widehat{GOC}\) là hai góc kề nhau nên \(\widehat{EOG}+\widehat{COG}=\widehat{COE}.\)
Suy ra \(\widehat{EOG}=\widehat{COE}-\widehat{COG}=60^o-40^o=20^o.\)
b) Do \(\widehat{COE}\) và \(\widehat{EOD}\) là hai góc kề nhau nên \(\widehat{COE}+\widehat{DOE}=\widehat{COD}.\)
Suy ra \(\widehat{DOE}=\widehat{COD}-\widehat{COE}=80^o-60^o=20^o.\)
Do đó \(\widehat{EOG}=\widehat{DOE}=20^o.\)
Mặt khác OE nằm giữa hai tia OG và OD nên OE là là tia phân giác của góc DOG.
\(\)
12. Ở Hình 20 có hai góc AOB và BOC là hai góc kề bù, \(\widehat{AOB}=3\widehat{BOC},\) \(\widehat{AOD}=\widehat{BOC}.\)
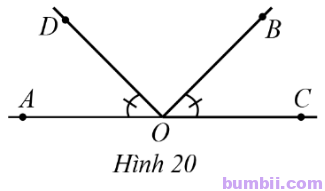
a) Tính số đo góc BOC.
b) Tia OB có là tia phân giác của góc COD hay không?
Giải
a) Ta có \(\widehat{AOB}+\widehat{BOC}=180^o\) (hai góc kề bù)
Mà \(\widehat{AOB}=3\widehat{BOC}\) nên \(3\widehat{BOC}+\widehat{BOC}=4\widehat{BOC}=180^o\)
Do đó \(\widehat{BOC}=180^o:4=45^o.\)
b) Do \(\widehat{AOD}=\widehat{BOC}\) mà \(\widehat{BOC}=45^o\) nên \(\widehat{AOD}=45^o.\)
Ta có \(\widehat{AOD}\) và \(\widehat{DOB}\) là hai góc kề nhau nên \(\widehat{BOD}+\widehat{BOC}=\widehat{COD}.\)
Mà \(\widehat{AOD}+\widehat{BOC}=180^o\) (hai góc kề bù) nên \(\widehat{AOD}+\widehat{BOD}+\widehat{BOC}=180^o.\)
Suy ra \(\widehat{BOD}=180^o-\widehat{AOD}-\widehat{BOC}\) \(=180^o-45^o-45^o=90^o.\)
Do đó hai góc BOD và BOC không bằng nhau.
Vậy OB không là tia phân giác của góc COD.
\(\)
13. Ở Hình 21 có \widehat{xOy}=70^o,\widehat{xOz}=120^o, hai tia Om và On lần lượt là tia phân giác của góc xOy và xOz. Tính số đo mỗi góc yOz, xOm, xOn, mOn.
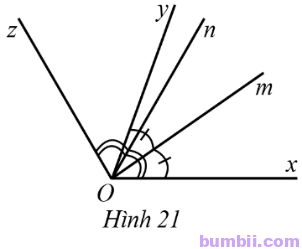
Giải
Do \(\widehat{xOy}\) và \(\widehat{yOz}\) là hai góc kề nhau nên \(\widehat{xOy}+\widehat{yOz}=\widehat{xOz}.\)
Suy ra \(\widehat{yOz}=\widehat{xOz}-\widehat{xOy}=120^o-70^o=50^o.\)
Do Om là tia phân giác của \(\widehat{xOy}\) nên \(\widehat{xOm}=\widehat{mOy}=\displaystyle\frac{1}{2}\widehat{xOy}=\displaystyle\frac{1}{2}.70^o=35^o.\)
Do On là tia phân giác của \(\widehat{xOz}\) nên \(\widehat{xOn}=\widehat{nOy}=\displaystyle\frac{1}{2}\widehat{xOz}=\displaystyle\frac{1}{2}.120^o=60^o.\)
Do \(\widehat{xOm}\) và \(\widehat{mOn}\) là hai góc kề nhau nên \(\widehat{xOm}+\widehat{mOn}=\widehat{xOn}.\)
Suy ra \(\widehat{mOn}=\widehat{xOn}-\widehat{xOm}=60^o-35^o=25^o.\)
Vậy \(\widehat{yOz}=50^o,\ \widehat{xOm}=35^o,\) \(\widehat{xOn}=60^o,\) \(\widehat{mOn}=25^o.\)
\(\)
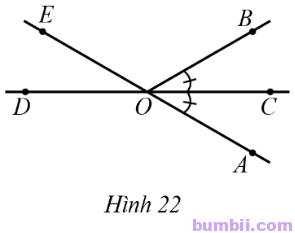
14. Ở Hình 22 có \(\widehat{AOB}=60^o,\) tia OC là tia phân giác của góc AOB.
a) Tính số đo mỗi góc BOC, BOE, COE, AOD.
b) Hai góc AOD và BOD có bằng nhau hay không?
Giải
a) Do tia OC là tia phân giác của góc AOB nên
\(\widehat{AOC}=\widehat{COB}=\displaystyle\frac{1}{2}\widehat{AOB}=\displaystyle\frac{1}{2}.60^o=30^o.\)
Ta có \(\widehat{AOB}+\widehat{BOE}=180^o;\) \(\widehat{AOC}+\widehat{COE}=180^o;\) \(\widehat{AOD}=\widehat{COE}=150^o\) (các cặp góc kề) nên
\(\widehat{BOE}=180^o-\widehat{AOB}=180^o-60^o=120^o.\)
\(\widehat{COE}=180^o-\widehat{AOC}=180^o-30^o=150^o.\)
Vậy \(\widehat{BOC}=30^o,\ \widehat{BOE}=120^o,\) \(\widehat{COE}=150^o,\) \(\widehat{AOD}=150^o.\)
b) Ta có \(\widehat{BOC}+\widehat{BOD}=180^o\) (hai góc kề bù)
\(\widehat{BOD}=180^o-\widehat{BOC}=180^o-30^o=150^o.\)
Do đó \(\widehat{AOD}=\widehat{BOD}=150^o.\)
\(\)
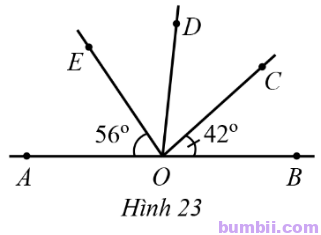
15. Ở Hình 23 có \(\widehat{BOC}=42^o,\) \(\widehat{AOD}=97^o,\) \(\widehat{AOE}=56^o.\)
a) Tính số đo mỗi góc BOD, DOE, COE.
b) Tia OD có là tia phân giác của góc COE hay không?
Giải
a) Ta có \(\widehat{AOD}+\widehat{DOB}=180^o\) (hai góc kề bù)
\(\widehat{DOB}=180^o-\widehat{AOD}=180^o-97^o=83^o.\)
Do \(\widehat{AOE}\) và \(\widehat{EOD}\) là hai góc kề nhau nên \(\widehat{AOE}+\widehat{EOD}=\widehat{AOD}.\)
Suy ra \(\widehat{EOD}=\widehat{AOD}-\widehat{AOE}=97^o-56^o=41^o.\)
Do \(\widehat{BOC}\) và \(\widehat{COD}\) là hai góc kề nhau nên \(\widehat{BOC}+\widehat{COD}=\widehat{BOD}.\)
Suy ra \(\widehat{COD}=\widehat{BOD}-\widehat{BOC}=83^o-42^o=41^o.\)
Do \(\widehat{EOD}\) và \(\widehat{COD}\) là hai góc kề nhau nên \(\widehat{EOD}+\widehat{COD}=\widehat{COE}.\)
Suy ra \(\widehat{EOC}=41^o+41^o=82^o.\)
Vậy \(\widehat{BOD}=83^o,\ \widehat{DOE}=41^o,\) \(\widehat{COE}=82^o.\)
b) Do \(\widehat{EOD}=\widehat{DOC}=41^o\) và tia OD nằm giữa hai tia OE và OC.
Do đó tia OD là tia phân giác của góc COE.
\(\)
Xem bài giải trước: Bài 1: Góc ở vị trí đặc biệt
Xem bài giải tiếp theo: Bài 3: Hai đường thẳng song song
Xem thêm các bài giải khác tại: Giải Bài tập Toán Lớp 7 Cánh Diều
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech
