Bài \(1\). Góc lượng giác trang \(7\) Sách giáo khoa Toán lớp \(11\) tập \(1\) Chân trời sáng tạo. Các em cùng Bumbii giải các bài tập sau:
Bài \(1\). Đổi số đo của các góc sau đây sang radian:
\(a)\) \(38^o\);
\(b)\) \(\ – \ 115^o\);
\(c)\) \(\left(\displaystyle \frac{3}{\pi}\right)^o\).
Trả lời:
\(a)\) Ta có: \(38^o = \displaystyle \frac{38\pi}{180} \text{ rad } = \displaystyle \frac{19\pi}{90} \text{ rad }\);
\(b)\) \(\ – \ 115^o = \ – \ \displaystyle \frac{115\pi}{180} \text{ rad } = \ – \ \displaystyle \frac{23\pi}{36} \text{ rad }\);
\(c)\) \(\left(\displaystyle \frac{3}{\pi}\right)^o = \displaystyle \frac{3\pi}{180\pi} \text{ rad } = \displaystyle \frac{1}{60} \text{ rad }\)
\(\)
Bài \(2\). Đổi số đo của các góc sau đây sang độ:
\(a)\) \(\displaystyle \frac{\pi}{12}\);
\(b)\) \(\ – \ 5\);
\(c)\) \(\displaystyle \frac{13\pi}{9}\).
Trả lời:
\(a)\) \(\displaystyle \frac{\pi}{12} = \left(\displaystyle \frac{\pi}{12}. \displaystyle \frac{180}{\pi}\right)^o = 15^o\)
\(b)\) \(\ – \ 5 = \left(\ – \ 5. \displaystyle \frac{180}{\pi}\right)^o \approx \ – \ 286,62^o\)
\(c)\) \(\displaystyle \frac{13\pi}{9} = \left(\displaystyle\frac{13\pi}{9}. \displaystyle \frac{180}{\pi}\right)^o = 260^o\)
\(\)
Bài \(3\). Biểu diễn các góc sau đây trên đường tròn lượng giác:
\(a)\) \(\displaystyle \frac{\ – \ 17\pi}{3}\);
\(b)\) \(\displaystyle \frac{13\pi}{4}\);
\(c)\) \(\ – \ 765^o\).
Trả lời:
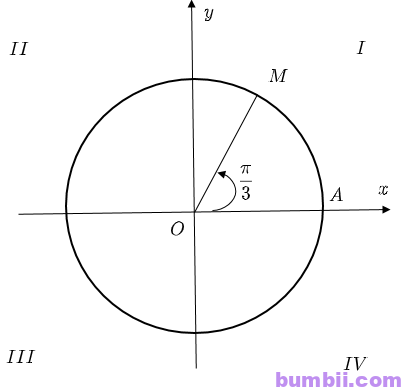
\(a)\) Ta có: \(\displaystyle \frac{\ – \ 17\pi}{3} = \displaystyle \frac{\pi}{3} + (\ – \ 3). 2\pi\)
Vậy điểm biểu diễn góc lượng giác có số đo \(\displaystyle \frac{\ – \ 17\pi}{3}\) là điểm \(M\) trên phần đường tròn lượng giác thuộc góc phần tư thứ nhất sao cho \(\widehat{AOM} = 60^o\)
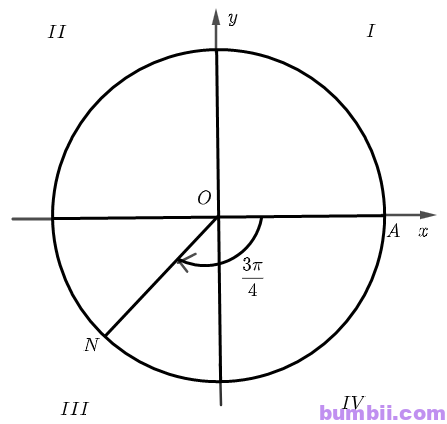
\(b)\) Ta có: \(\displaystyle \frac{13\pi}{4} = \ – \ \displaystyle \frac{3\pi}{4} + 2. 2\pi\)
Vậy điểm biểu diễn góc lượng giác có số đo \(\displaystyle \frac{17\pi}{4}\) là điểm \(N\) trên phần đường tròn lượng giác thuộc góc phần tư thứ ba sao cho \(\widehat{AON} = \displaystyle \frac{3\pi}{4}\)
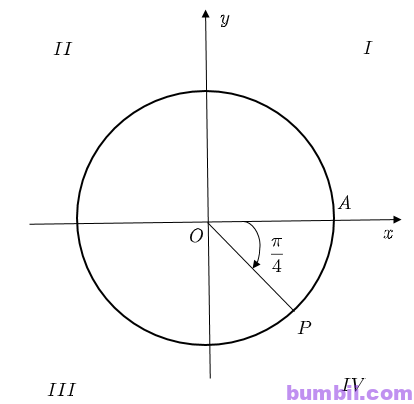
\(c)\) \(\ – \ 765^o = \ – \ 45^o \ – \ 2. 360^o\)
Vậy điểm biểu diễn góc lượng giác có số đo là \(\ – \ 765^o\) là điểm \(P\) trên phần đường tròn lượng giác thuộc góc phần tư thứ tư sao cho \(\widehat{AOP} = 45^o\)
\(\)
Bài \(4\). Góc lượng giác \(\displaystyle \frac{31\pi}{7}\) có cùng điểm biểu diễn trên đường tròn lượng giác với góc lượng giác nào sau đây?
\(\displaystyle \frac{3\pi}{7}; \displaystyle \frac{10\pi}{7}; \displaystyle \frac{\ – \ 25\pi}{7}\).
Trả lời:
Hai góc lượng giác( \(\alpha\) và \(\beta\)) có cùng điểm biểu diễn trên đường tròn lượng giác khi và chỉ khi:
\(\alpha = \beta + k. 2\pi\) (\(k \in \mathbb{Z}\))
Ta có: \(\displaystyle \frac{31\pi}{7} = \displaystyle \frac{3\pi}{7} + 2. 2\pi\) thỏa mãn \(k = 2 \in \mathbb{Z}\)
\(\displaystyle \frac{31\pi}{7} = \displaystyle \frac{10\pi}{7} + \displaystyle \frac{3}{2}. 2\pi\) không thỏa mãn \(k = \displaystyle \frac{3}{2} \notin \mathbb{Z}\)
\(\displaystyle \frac{31\pi}{7} = \ – \ \displaystyle \frac{\ – \ 25\pi}{7} + 4. 2\pi\) thỏa mãn \(k = 4 \in \mathbb{Z}\)
Suy ra, góc lượng giác \(\displaystyle \frac{31\pi}{7}\) có cùng điểm biểu diễn trên đường tròn lượng giác với các góc lượng giác: \(\displaystyle \frac{3\pi}{7}\) và \(\displaystyle \frac{\ – \ 25\pi}{7}\) (Điểm biểu diễn thuộc góc phần tư thứ nhất)
\(\)
Bài \(5\). Viết công thức số đo tổng quát của các góc lượng giác \((OA, OM)\) và \((OA, ON)\) trong Hình \(14\).
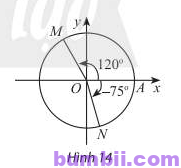
Trả lời:
Ta có: \(\widehat{AOM} = 120^o, \widehat{AON} = \ – \ 75^o\)
Suy ra \((OA, OM) = 120^o + k. 360^o\) (\(k \in \mathbb{Z}\))
\((OA, ON) = \ – \ 75^o + k. 360^o\) (\(k \in \mathbb{Z}\))
\(\)
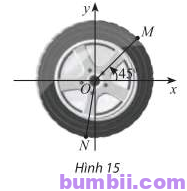
Bài \(6\). Trong Hình \(15\), mâm bánh xe ô tô được chia thành \(5\) phần bằng nhau. Viết công thức số đo tổng quát của góc lượng giác \((Ox, ON)\).
Trả lời:
Do mâm bánh xe ô tô được chia thành \(5\) phần bằng nhau nên số đo góc của mỗi phần sẽ là:
\(360^o : 5 = 72^o\)
Theo Hình \(15\), \(\widehat{MON}\) tương ứng với \(2\) trong \(5\) phần đã chia hay \(\widehat{MON} = 2. 72^o = 144^o\)
Mà \(\widehat{xOM} = 45^o\)
Suy ra \(\widehat{xON} = 144 \ – \ 45^o = 99^o\)
Vậy công thức số đo tổng quát của góc lượng giác \((Ox, ON) = \ – \ 99^o + k. 360^o\) (\(k \in \mathbb{Z}\))
\(\)
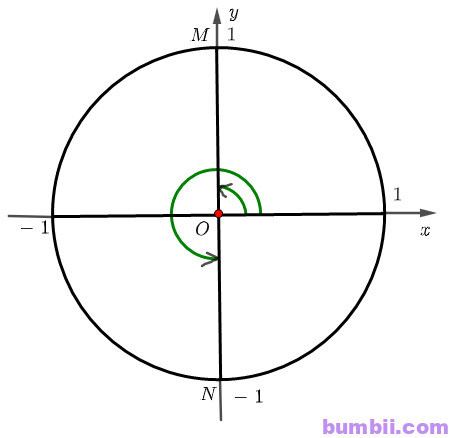
Bài \(7\). Trên đường tròn lượng giác, hãy biểu diễn các góc lượng giác có số đo có dạng là:
\(a)\) \(\displaystyle \frac{\pi}{2} + k\pi\) (\(k \in \mathbb{Z}\));
\(b)\) \(k\displaystyle \frac{\pi}{4}\) (\(k \in \mathbb{Z}\)).
Trả lời:
\(a)\) \(\displaystyle \frac{\pi}{2} + k\pi\) (\(k \in \mathbb{Z}\))
Với \(k = 0\), góc lượng giác có số đo \(\displaystyle \frac{\pi}{2}\) được biểu diễn bởi điểm \(M\)
Với \(k = 1\), góc lượng giác có số đo \(\displaystyle \frac{\pi}{2} + \pi\) được biểu diễn bởi điểm \(N\)
Với \(k = 2\), góc lượng giác có số đo \(\displaystyle \frac{\pi}{2} + 2\pi\) được biểu diễn bởi điểm \(M\)
Với \(k = 3\), góc lượng giác có số đo \(\displaystyle \frac{\pi}{2} + 3\pi = \displaystyle \frac{3\pi}{2} + 2\pi\) được biểu diễn bởi điểm \(N\)
Vậy với \(k \in \mathbb{Z}, k\) chẵn, góc lượng giác đã cho được biểu diễn bởi điểm \(M\); khi \(k \in \mathbb{Z}, k\) lẻ thì góc lượng giác đã cho được biểu diễn bởi điểm \(N\). Khi đó ta có hình vẽ biểu diễn sau đây:
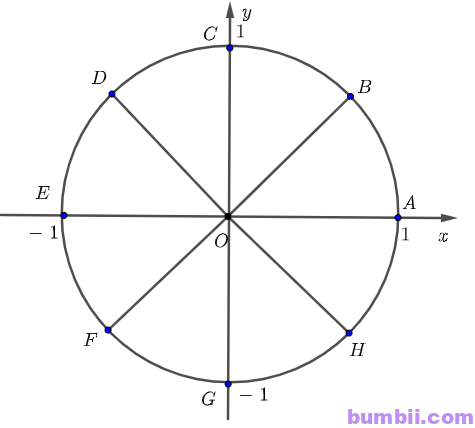
\(b)\) \(k\displaystyle \frac{\pi}{4}\) (\(k \in \mathbb{Z}\))
Với \(k = 0\), góc lượng giác có số đó là \(0\), được biểu diễn bởi điểm \(A\)
Với \(k = 1\), góc lượng giác có số đó là \(\displaystyle \frac{\pi}{4}\), được biểu diễn bởi điểm \(B\)
Với \(k = 2\), góc lượng giác có số đo là \(2\displaystyle \frac{\pi}{4} = \displaystyle \frac{\pi}{2}\), được biểu diễn bởi điểm \(C\)
Với \(k = 3\), góc lượng giác có số đo là \(\displaystyle \frac{3\pi}{4}\), được biểu diễn bởi điểm \(D\)
Với \(k = 4\), góc lượng giác có số đo là \(4\displaystyle \frac{\pi}{4} = \pi\), được biểu diễn bởi điểm \(E\)
Với \(k = 5\), góc lượng giác có số đó là \(\displaystyle \frac{5\pi}{4}\), được biểu diễn bởi điểm \(F\)
Với \(k = 6\), góc lượng giác có số đó là \(\displaystyle \frac{6\pi}{4} = \displaystyle \frac{3\pi}{2}\), được biểu diễn bởi điểm \(G\)
Với \(k = 7\), góc lượng giác có số đó là \(\displaystyle \frac{7\pi}{4}\), được biểu diễn bởi điểm \(H\)
Với \(k = 8\), góc lượng giác có số đó là \(\displaystyle \frac{8\pi}{4} = 2\pi\), được biểu diễn bởi điểm \(A\)
Vậy các góc lượng giác có số đo \(k\displaystyle \frac{\pi}{4}\) (\(k \in \mathbb{Z}\)) được biểu diễn bởi các điểm \(A, B, C, D, E, F, G, H\). Ta có hình vẽ biểu diễn sau đây:
\(\)
Bài \(8\). Vị trí các điểm \(B, C, D\) trên cánh quạt động cơ máy bay trong Hình \(16\) có thể được biểu diễn cho các góc lượng giác nào sau đây?
\(\displaystyle \frac{\pi}{2} + k\displaystyle \frac{2\pi}{3} (k \in \mathbb{Z}); \displaystyle \frac{\ – \ \pi}{6} + k\displaystyle \frac{2\pi}{3} (k \in \mathbb{Z}); \displaystyle \frac{\pi}{2} + k\displaystyle \frac{\pi}{3} (k \in \mathbb{Z}\))
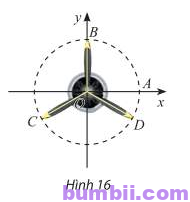
Trả lời:
\(*\) Xét các góc lượng giác có số đo \(\displaystyle \frac{\pi}{2} + k\displaystyle \frac{2\pi}{3}\) (\(k \in \mathbb{Z}\))
Với \(k = 0\), góc lượng giác có số đo bằng \(\displaystyle \frac{\pi}{2}\) được biểu diễn bởi điểm \(B\)
Với \(k = 1\), góc lượng giác có số đo bằng \(\displaystyle \frac{\pi}{2} + \displaystyle \frac{2\pi}{3} = \displaystyle \frac{7\pi}{6}\) được biểu diễn bởi điểm \(C\)
Với \(k = 2\), góc lượng giác có số đo bằng \(\displaystyle \frac{\pi}{2} + 2. \displaystyle \frac{2\pi}{3} = \displaystyle \frac{11\pi}{6}\) được biểu diễn bởi điểm \(D\)
Với \(k = 3\), góc lượng giác có số đo bằng \(\displaystyle \frac{\pi}{2} + 3. \displaystyle \frac{2\pi}{3} = \displaystyle \frac{\pi}{2} + 2\pi\) được biểu diễn bởi điểm \(B\)
Vậy các góc lượng giác có số đo \(\displaystyle \frac{\pi}{2} + k\displaystyle \frac{2\pi}{3}\) (\(k \in \mathbb{Z}\)) được biểu diễn bởi các điểm \(B, C, D\)
\(*\) Xét các góc lượng giác có số đo \(\displaystyle \frac{\ – \ \pi}{6} + k\displaystyle \frac{2\pi}{3}\) (\(k \in \mathbb{Z}\))
Với \(k = 0\), góc lượng giác có số đo bằng \(\ – \ \displaystyle \frac{\pi}{6}\) được biểu diễn bởi điểm \(D\).
Với \(k = 1\), góc lượng giác có số đo bằng \(\ – \ \displaystyle \frac{\pi}{6} + \displaystyle \frac{2\pi}{3} = \displaystyle \frac{\pi}{2}\) được biểu diễn bởi điểm \(B\)
Với \(k = 2\), góc lượng giác có số đo bằng \(\ – \ \displaystyle \frac{\pi}{6} + 2. \displaystyle \frac{2\pi}{3} = \displaystyle \frac{7\pi}{6}\) được biểu diễn bởi điểm \(C\)
Với \(k = 3\), góc lượng giác có số đo bằng \(\ – \ \displaystyle \frac{\pi}{6} + 3. \displaystyle \frac{2\pi}{3} = \displaystyle \frac{\ – \ \pi}{6} + 2\pi\) được biểu diễn bởi điểm \(D\)
Với \(k = 4\), góc lượng giác có số đo bằng \(\ – \ \displaystyle \frac{\pi}{6} + 4. \displaystyle \frac{2\pi}{3} = \displaystyle \frac{7\pi}{6}\) được biểu diễn bởi điểm \(C\)
Vậy các góc lượng giác có số đo \(\displaystyle \frac{\ – \ \pi}{6} + k\displaystyle \frac{2\pi}{3}\) (\(k \in \mathbb{Z}\)) được biểu diễn bởi các điểm \(B, C, D\)
\(*\) Xét các góc lượng giác có số đo \(\displaystyle \frac{\pi}{2} + k\displaystyle \frac{\pi}{3}\) (\(k \in \mathbb{Z}\))
Với \(k = 0\), góc lượng giác có số đo \(\displaystyle \frac{\pi}{2}\) được biểu diễn bởi điểm \(B\)
Với \(k = 1\), góc lượng giác có số đo \(\displaystyle \frac{\pi}{2} + \displaystyle \frac{\pi}{3} = \displaystyle \frac{5\pi}{6}\) được biểu diễn bởi điểm \(M\)
Với \(k = 2\), góc lượng giác có số đo \(\displaystyle \frac{\pi}{2} + 2. \displaystyle \frac{\pi}{3} = \displaystyle \frac{7\pi}{6}\) được biểu diễn bởi điểm \(C\)
Với \(k = 3\), góc lượng giác có số đo \(\displaystyle \frac{\pi}{2} + 3. \displaystyle \frac{\pi}{3} = \displaystyle \frac{3\pi}{2}\) được biểu diễn bởi điểm \(N\)
Với \(k = 4\), góc lượng giác có số đo \(\displaystyle \frac{\pi}{2} + 4. \displaystyle \frac{\pi}{3} = \displaystyle \frac{11\pi}{6}\) được biểu diễn bởi điểm \(D\)
Với \(k = 5\), góc lượng giác có số đo \(\displaystyle \frac{\pi}{2} + 5. \displaystyle \frac{\pi}{3} = \displaystyle \frac{13\pi}{6} = \displaystyle \frac{\ – \ \pi}{6} + 2\pi\) được biểu diễn bởi điểm \(P\)
Với \(k = 6\), góc lượng giác có số đo \(\displaystyle \frac{\pi}{2} + 6. \displaystyle \frac{\pi}{3} = \displaystyle \frac{\pi}{2} + 2\pi\) được biểu diễn bởi điểm \(B\)
Vậy các điểm \(B, C, D\) không thể biểu diễn cho các góc lượng giác có số đo \(\displaystyle \frac{\pi}{2} + k\displaystyle \frac{\pi}{3}\) (\(k \in \mathbb{Z}\))
\(\)
Bài \(9\). Hải lí là một đơn vị chiều dài hàng hải, được tính bằng độ dài một cung chắn một góc \(\alpha = \left(\displaystyle \frac{1}{60}\right)^o\) của đường kinh tuyến (Hình \(17\)). Đổi số đo \(\alpha\) sang radian và cho biết \(1\) hải lí bằng khoảng bao nhiêu kilômét, biết bán kính trung bình của Trái Đất là \(6371\) km. Làm tròn kết quả đến hàng phần trăm.
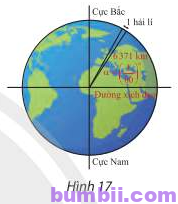
Trả lời:
Ta có: \(\alpha = \left(\displaystyle \frac{1}{60}\right)^o = \displaystyle \frac{1}{60}. \displaystyle \frac{\pi}{180} \text{ rad } = \displaystyle \frac{\pi}{10800} \text{ rad }\)
Độ dài cung chắn góc \(\alpha\) bằng:
\(R. \alpha = 6371. \displaystyle \frac{\pi}{10800} \approx 1,85\) (km)
Vậy \(1\) hải lí bằng \(1,85\) km.
\(\)
Xem bài giải trước:
Xem bài giải tiếp theo: Bài 2 – Giá trị lượng giác của một góc lượng giác
Xem các bài giải khác: Giải bài tập SGK Toán Lớp 11 Chân trời sáng tạo
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech

Hạnh phúc đạt được khi bạn ngừng chờ đợi điều đó xảy ra và thực hiện các bước để biến nó thành hiện thực.