Bài \(1\). Đường thẳng và mặt phẳng trong không gian trang \(85\) SGK Toán lớp \(11\) Tập \(1\) Cánh diều. Các em cùng Bumbii giải các bài tập sau:
Bài \(1\). Khi trát tường, dụng cụ không thể thiếu của người thợ là thước dẹt dài (Hình \(28\)). Cộng dụng của thước dẹt này là gì? Giải thích.

Trả lời:
Công dụng của thước dẹt là: Kiểm tra xem mặt tường đã thật sự phẳng chưa.
Giải thích: Áp thước dẹt vào mặt tường, nếu toàn bộ thước áp khít vào mặt tường thì tức là mặt tường đã được trát phẳng. Còn nếu thước không khít mặt tường thì ta cần bổ sung thêm vữa trát vào vị trí chưa khít đó.
\(\)
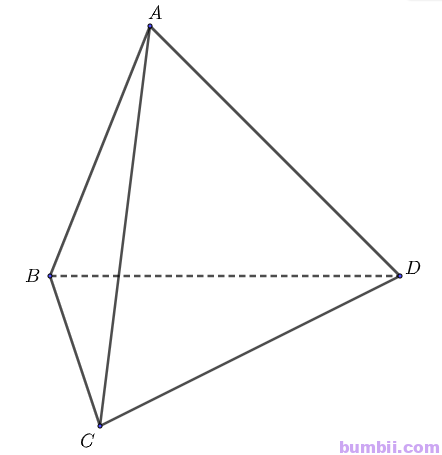
Bài \(2\). Hình \(29\) là hình ảnh của chặn giấy bằng gỗ có bốn mặt phân biệt là các tam giác. Vẽ hình biểu diễn của chặn giấy bằng gỗ đó.

Trả lời:
Hình biểu diễn của chặn giấy bằng gỗ là hình tứ diện:
\(\)
Bài \(3\). Cho ba đường thẳng \(a, b, c\) không cùng nằm trong một mặt phẳng và đôi một cắt nhau. Chứng minh rằng ba đường thẳng \(a, b, c\) cùng đi qua một điểm, hay còn gọi là ba đường thẳng đồng quy.
Trả lời:
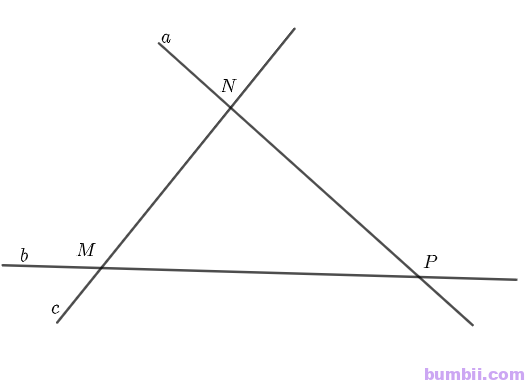
Giả sử \(a \cap b = M, a \cap c = N, b \cap c = P\)
trong đó \(M, N, P\) không trùng nhau.
Khi đó, \(P, N \in a\)
Mặt khác, \(N \in c, P \in b\)
Do đó \(PN \subset (b, c)\) hay đường thẳng \(a \subset (b, c)\)
Suy ra ba đường thẳng \(a, b, c\) đồng phẳng trái với giả thiết.
Vậy ba đường thẳng \(a, b, c\) cùng đi qua một điểm.
\(\)
Bài \(4\). Cho hình chóp \(S.ABCD\) có \(AC\) cắt \(BD\) tại \(O\) và \(AB\) cắt \(CD\) tại \(P\). Điểm \(M\) thuộc cạnh \(SA\) (\(M\) khác \(S\), \(M\) khác \(A\)). Gọi \(N\) là giao điểm của \(MP\) và \(SB\), \(I\) là giao điểm của \(MC\) và \(DN\). Chứng minh rằng \(S, O, I\) thẳng hàng.
Trả lời:
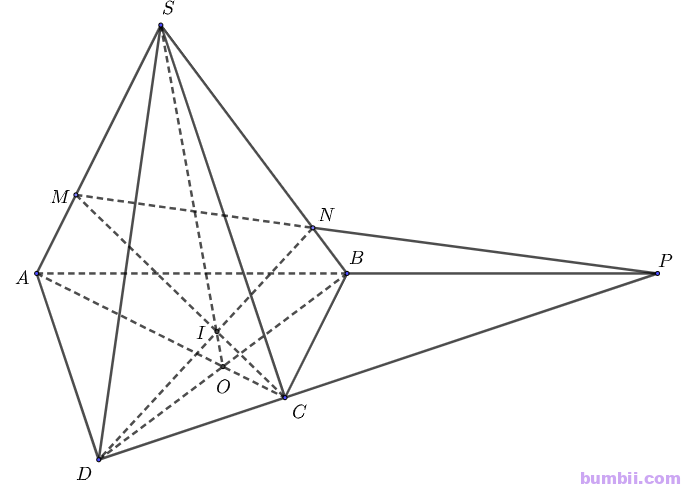
Ta có: \(O\) là giao điểm của \(AC\) và \(BD\)
Mà \(AC \subset (SAC), BD \subset (SBD)\)
\(\Rightarrow O\) là giao điểm của hai mặt phẳng \((SAC)\) và \((SBD)\).
Lại có \(S\) là điểm chung của hai mặt phẳng \((SAC)\) và \((SBD)\).
Do đó \(SO\) là giao tuyến của \((SAC)\) và \((SBD)\) (\(1\))
Xét mặt phẳng \((MNCD)\) có:
\(I\) là giao điểm của \(MC\) và \(DB\)
\(MC \subset (SAC)\)
\(DN \subset (SBD)\).
Suy ra \(I\) là giao điểm của \((SAC)\) và \((SBD)\). (\(2\))
Từ (\(1\)) và (\(2\)) suy ra \(I \in SO\)
Vậy \(S, I, O\) thẳng hàng.
\(\)
Bài \(5\). Cho hình chóp \(S.ABC\). Các điểm \(M,N\) lần lượt thuộc các cạnh \(SA, SC\) sao cho \(MA = 2MS, NS = 2NC\).
\(a)\) Xác định giao điểm của \(MN\) với mặt phẳng \((ABC)\).
\(b)\) Xác định giao tuyến của mặt phẳng \((BMN)\) với mặt phẳng \((ABC)\).
Trả lời:
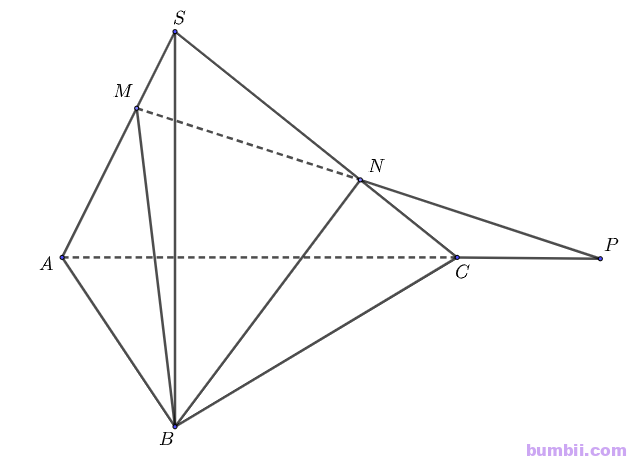
\(a)\) Trong mặt phẳng \((SAC)\), gọi \(P\) là giao điểm của \(MN\) và \(AC\).
Mà \(AC \subset (ABC)\).
Suy ra \(P\) là giao điểm của \(MN\) và mặt phẳng \((ABC)\).
\(b)\) Ta có: \(P \in AC\), mà \(AC \subset (ABC)\) nên \(P \in (ABC)\).
Lại có \(P \in MN, MN \subset (BMN)\) nên \(P \in (BMN)\).
Do đó, \(P\) là giao điểm của \((BMN)\) và \((ABC)\) (\(1\))
Mặt khác \(B \in (BMN), B \in (ABC)\) nên \(B\) là giao điểm của \((BMN)\) và \((ABC)\) (\(2\))
Từ (\(1\)) và (\(2\)) suy ra:
\(BP\) là giao tuyến của hai mặt phẳng \((BMN)\) và \((ABC)\).
\(\)
Bài \(6\). Cho hình chóp tứ giác \(S.ABCD\) có đáy không là hình thang. Gọi \(M\) là trung điểm của \(SA\).
\(a)\) Xác định giao điểm của \(CD\) với mặt phẳng \((SAB)\).
\(b)\) Xác định giao tuyến của hai mặt phẳng \((SAB)\) và \((SCD)\).
\(c)\) Xác định giao tuyến của hai mặt phẳng \((MCD)\) và \((SBC)\).
Trả lời:
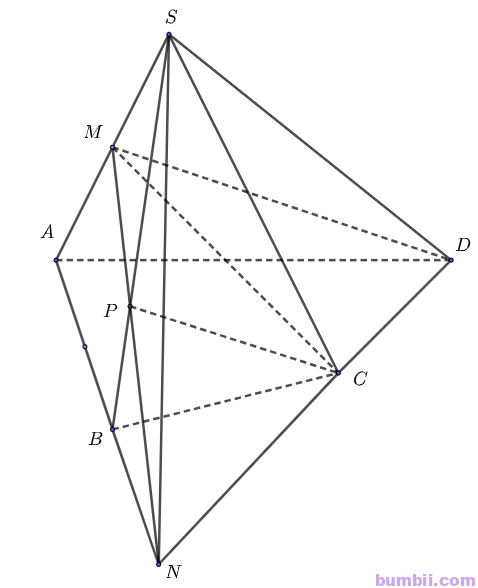
\(a)\) Trong mặt phẳng \((ABCD)\), gọi \(N\) là giao điểm của \(AB\) và \(CD\)..
Mà \(AB \subset (SAB)\)
Suy ra \(N\) là giao điểm của \(CD\) và \((SAB)\).
\(b)\) Ta có: \(N\) là giao điểm của \(AB\) và \(CD\)
\(AB \subset (SAB), CD \subset (SCD)\)
Do đó, \(N\) là giao điểm của \((SAB)\) và \((SCD)\).
Lại có: \(S \in (SAB), S \in (SCD)\) nên \(S\) là giao điểm của \((SAB)\) và \((SCD)\).
Vì vậy, \(SN\) là giao tuyến của hai mặt phẳng \((SAB)\) và \((SCD)\).
\(c)\) Ta có \(C \in (SBC), C \in (MCD)\) nên \(C\) là giao điểm của \((SBC)\) và \((MCD)\).
Trong mặt phẳng \((SAB)\), gọi \(P\) là giao điểm của \(MN\) và \(SB\).
Mà \(MN \subset (MCD), SB \subset (SBC)\)
Suy ra \(P\) là giao điểm của \((SBC)\) và \((MCD)\)
Vậy \(CP\) là giao tuyến của hai mặt phẳng \((SBC)\) và \((MCD)\).
\(\)
Bài \(7\). Cho tứ diện \(ABCD\). Gọi \(I\) là trung điểm cạnh \(CD\). Gọi \(M, N\) lần lượt là trọng tâm các tam giác \(BCD, CDA\).
\(a)\) Chứng minh rằng các điểm \(M, N\) thuộc mặt phẳng \((ABI)\).
\(b)\) Gọi \(G\) là giao điểm của \(AM\) và \(BN\). Chứng minh rằng: \(\displaystyle \frac{GM}{GA} = \displaystyle \frac{GN}{GB} = \displaystyle \frac{1}{3}\).
\(c)\) Gọi \(P, Q\) lần lượt là trọng tâm các tam giác \(DAB, ABC\). Chứng minh rằng các đường thẳng \(CP, DQ\) cùng đi qua điểm \(G\) và \(\displaystyle \frac{GP}{GC} = \displaystyle \frac{GQ}{GD} = \displaystyle \frac{1}{3}\).
Trả lời:
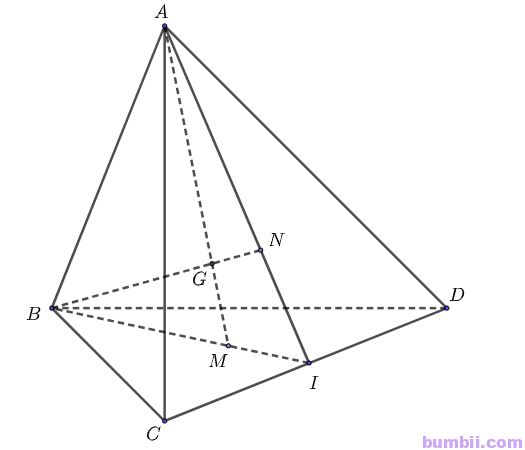
\(a)\) Xét tam giác \(ACD\) có:
\(I\) là trung điểm \(CD\) nên \(AI\) là trung tuyến của tam giác \(ACD\).
\(N\) là trọng tâm tam giác \(ACD\) nên \(N \in AI\).
Mà \(AI \subset (ABI)\)
Do đó \(N \in (ABI)\).
Xét tam giác \(BCD\) có \(BI\) là trung tuyến.
\(M\) là trọng tâm tam giác \(BCD\) nên \(M \in BI\).
Mà \(BI \subset (ABI)\)
Do đó \(M \in (ABI)\)
\(b)\) \(M\) là trọng tâm tam giác \(BCD\) nên:
\(\displaystyle \frac{MI}{BI} = \displaystyle \frac{1}{3}\)
\(N\) là trọng tâm tam giác \(ACD\) nên:
\(\displaystyle \frac{NI}{AI} = \displaystyle \frac{1}{3}\)
Xét tam giác \(ABI\) có:
\(\displaystyle \frac{MI}{BI} = \displaystyle \frac{NI}{AI} = \displaystyle \frac{1}{3}\)
\(\Rightarrow MN // AB\)
Xét tam giác \(ABI\) có \(MN // AB\) nên ta có:
\(\displaystyle \frac{MN}{AB} = \displaystyle \frac{NI}{AI} = \displaystyle \frac{MI}{AI} = \displaystyle \frac{1}{3}\).
Suy ra \(\displaystyle \frac{GM}{GA} = \displaystyle \frac{GN}{GB} = \displaystyle \frac{MN}{AB} = \displaystyle \frac{1}{3}\)
\(c)\) Gọi \(G_1\) là giao điểm của \(AM\) và \(CP\), \(G_2\) là giao điểm của \(AM\) và \(DQ\).
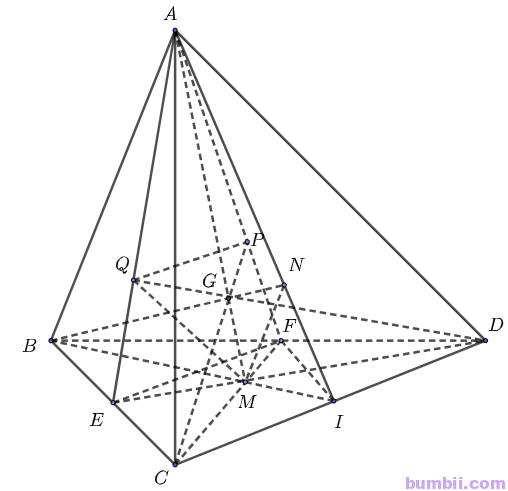
Chứng minh tương tự câu \(b)\) ta được:
\(\displaystyle \frac{G_1M}{G_1A} = \displaystyle \frac{G_1P}{G_1C} = \displaystyle \frac{PM}{AC} = \displaystyle \frac{1}{3}\)
\(\displaystyle \frac{G_2M}{G_2A} = \displaystyle \frac{G_2Q}{G_2D} = \displaystyle \frac{QM}{AD} = \displaystyle \frac{1}{3}\)
Suy ra \(\displaystyle \frac{GM}{GA} = \displaystyle \frac{G_1M}{G_1A} = \displaystyle \frac{G_2M}{G_2A} = \displaystyle \frac{1}{3}\)
Mà \(G, G_1, G_2\) cùng thuộc \(AM\).
Do đó \(G \ G_1 \ G_2\).
Hay các đường thẳng \(CP\) và \(DQ\) cùng đi qua điểm \(G\).
Xét tam giác \(ABC\) có \(AE\) là trung tuyến (\(E \in BC\)) và \(Q\) là trọng tâm nên ta có:
\(\displaystyle \frac{AQ}{AE} = \displaystyle \frac{2}{3}\) (\(1\))
Xét tam giác \(ABD\) có \(AF\) là trung tuyến (\(F \in BD\)) và \(P\) là trọng tâm nên ta có:
\(\displaystyle \frac{AP}{AF} = \displaystyle \frac{2}{3}\) (\(2\))
Từ (\(1\)) và (\(2\)) suy ra \(PQ // EF\)
Mà \(EF // CD\) nên \(PQ // CD\)
Khi đó, theo hệ quả định lí Thales ta có:
\(\displaystyle \frac{GP}{GC} = \displaystyle \frac{GQ}{GD} = \displaystyle \frac{PQ}{CD} = \displaystyle \frac{PQ}{2EF} = \displaystyle \frac{1}{2}. \displaystyle \frac{2}{3} = \displaystyle \frac{1}{3}\)
Bài 1. Đường thẳng và mặt Bài 1. Đường thẳng và mặt Bài 1. Đường thẳng và mặt
Xem bài giải trước: Bài tập cuối chương III
Xem bài giải tiếp theo: Bài 2 – Hai đường thẳng song song trong không gian
Xem các bài giải khác: Giải bài tập SGK Toán Lớp 11 Cánh Diều
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech

Hạnh phúc đạt được khi bạn ngừng chờ đợi điều đó xảy ra và thực hiện các bước để biến nó thành hiện thực.