Bài tập cuối chương V

Bài tập cuối chương \(V\) trang \(25\) SGK Toán lớp \(11\) tập \(II\) Cánh diều. Các em cùng Bumbii giải các bài tập sau:

Bài \(1\). Người ta tiến hành phỏng vấn \(40\) người về một mẫu áo sơ mi mới. Người điều tra yêu cầu cho điểm mẫu áo đó theo thang điểm \(100\). Kết quả được trình bày trong Bảng \(16\).

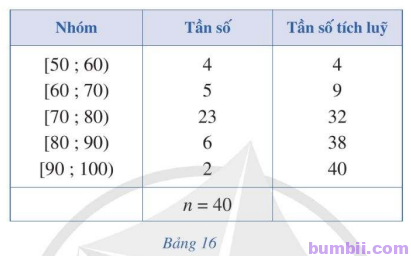
\(a)\) Trung vị của mẫu số liệu ghép nhóm trên gần nhất với giá trị:
\(A. 74\).
\(B. 75\).
\(C. 76\).
\(D. 77\).
\(b)\) Tứ phân vị của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng đơn vị) là:
\(A. Q_1 \approx 71; Q_2 \approx 76; Q_3 \approx 78\).
\(B. Q_1 \approx 71; Q_2 \approx 75; Q_3 \approx 78\).
\(C. Q_1 \approx 70; Q_2 \approx 76; Q_3 \approx 79\).
\(D. Q_1 \approx 70; Q_2 \approx 75; Q_3 \approx 79\).
\(c)\) Mốt của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng đơn vị) là:
\(A. 73\).
\(B. 74\).
\(C. 75\).
\(D. 76\).

Trả lời:

\(a)\) Trung vị của mẫu số liệu là:

\(M_e = r + \left(\displaystyle \frac{\frac{n}{2} \ – \ cf_{k \ – \ 1}}{n{k}}\right) . d = 70 + \left(\displaystyle \frac{20 \ – \ 9}{23}\right) .10 \approx 74,8\)

Chọn đáp án \(B\)

\(b)\) Tứ phân vị thứ hai \(Q_2 \approx 75\)

Tứ phân vị thứ nhất là:

\(Q_1 = s + \left(\displaystyle \frac{\frac{n}{4} \ – \ cf_{p \ – \ 1}}{n_p} \right). h = 70 + \displaystyle \frac{10 \ – \ 9}{23}. 10 \approx 70\)

Chọn đáp án \(D\).

\(c)\) Mốt của mẫu số liệu là:

\(M_0 = u + \displaystyle \frac{n_i \ – \ n_{i \ – \ 1}}{2n_i \ – \ n_{i \ – \ 1} \ – \ n_{i + 1}} . g = 70 + \displaystyle \frac{23 \ – \ 5}{2. 23 \ – \ 5 \ – \ 6}. 10 \approx 75\)

Chọn đáp án \(C\).

\(\)

Bài \(2\). Chọn ngẫu nhiên hai số khác nhau từ \(21\) số nguyên dương đầu tiên. Xác suất để chọn được hai số có tổng là một số chẵn bằng:
\(A. \displaystyle \frac{11}{21}\).
\(B. \displaystyle \frac{221}{441}\).
\(C. \displaystyle \frac{10}{21}\).
\(D. \displaystyle \frac{1}{2}\).

Trả lời:

Mỗi cách chọn ngẫu nhiên hai số khác nhau từ \(21\) số là một tổ hợp chập hai của \(21\) phần tử.

Do đó số phần tử của không gian mẫu là số các tổ hợp chập \(2\) của \(21\) phần tử và bằng

\(n(\Omega) = C_{21}^2 = \displaystyle \frac{21!}{2!. 19!} = 210\)

Số các số chẵn trong \(21\) số nguyên dương là \(10\)

Số các số chẵn trong \(21\) số nguyên dương là \(11\).

Để chọn được hai số có tổng là một số chẵn, xảy ra hai trường hợp sau:

Trường hợp \(1\): Hai số được chọn là hai số chẵn

Số cách chọn là: \(C_{10}^2 = 45\) (cách)

Trường hợp \(2\): Hai số được chọn là hai số lẻ

Số cách chọn là: \(C_{11}^2 = 55\) (cách)

Suy ra, số cách để chọn được hai số có tổng là một số chẵn là:

\(P = \displaystyle \frac{45 + 55}{210} = \displaystyle \frac{10}{21}\)

Chọn đáp án \(C\).

\(\)

Bài \(3\). Mẫu số liệu dưới đây ghi lại độ dài quãng đường di chuyển trong một tuần (đơn vị: kilômét) của \(40\) chiếc ôtô:

\(a)\) Lập bảng tần số ghép nhóm bao gồm cả tần số tích lũy với năm nhóm ứng với năm nửa khoảng:
\([100; 120), [120; 140), [140; 160), [160; 180), [180; 200)\).
\(b)\) Xác định số trung bình cộng, trung vị, tứ phân vị của mẫu số liệu ghép nhóm trên.
\(c)\) Mốt của mẫu số liệu ghép nhóm trên là bao nhiêu?

Trả lời:

\(a)\) Bảng tần số ghép nhóm bao gồm cả tần số tích luỹ với năm nhóm ứng với năm nửa khoảng là:

\(b)\) Số trung bình cộng:

\(\overline{x} = \displaystyle \frac{1}{40}. (110. 4 + 130. 15 + 150. 14 + 170. 5 + 190. 2)\)

\(= 145,5\)

Trung vị \(M_e = r + \left(\displaystyle \frac{\frac{n}{2} \ – \ cf_{k \ – \ 1}}{n_k}\right). d\)

\(= 140 + \left(\displaystyle \frac{20 \ – \ 14}{19}\right). 20 = \displaystyle \frac{2780}{19}\)

Suy ra tứ phân vị thứ hai \(Q_2 = M_e = \displaystyle \frac{2780}{19}\)

Tứ phân vị thứ nhất là:

\(Q_1 = 120 + \left(\displaystyle \frac{10 \ – \ 4}{10}\right). 20 = 132\)

Tứ phân vị thứ ba là:

\(Q_3 = 140 + \left(\displaystyle \frac{30 \ – \ 14}{19}\right). 20 = \displaystyle \frac{2980}{19}\)

\(c)\) Mốt của mẫu số liệu là:

\(M_0 = 140 + \left(\displaystyle \frac{19 \ – \ 10}{2. 19 \ – \ 10 \ – \ 5}\right). 20 = \displaystyle \frac{3229}{23}\)

\(\)

Bài \(4\). Bạn Dũng và bạn Hương tham gia đội văn nghệ của nhà trường. Nhà trường chọn từ đội văn nghệ đó một bạn nam và một bạn nữ để lập tiết mục song ca. Xác suất được chọn vào tiết mục song ca của Dũng và Hương lần lượt là \(0,7\) và \(0,9\). Tính xác suất của các biến cố sau:
\(a) A:\) “Cả hai bạn được chọn vào tiết mục song ca”.
\(b) B:\) “Có ít nhất một bạn được chọn vào tiết mục song ca”.
\(c) C:\) “Chỉ có bạn Hương được chọn vào tiết mục song ca”.

Trả lời:

Xét hai biến cố:

\(M:\) “Bạn Dũng được chọn vào tiết mục song ca”

\(\Rightarrow P(M) = 0,9\)

\(N:\) “Bạn Hương được chọn vào tiết mục song ca”

\(\Rightarrow P(N) = 0,7\)

\(a)\) Do \(A = M \cap N\)

\(\Rightarrow P(A) = P(M). P(N) = 0,9. 0,7 = 0,63\)

\(b)\) Do \(B = M \cup N\)

\(\Rightarrow P(B) = P(M) + P(N) \ – \ P(M \cap N) = 0,9 + 0,7 \ – \ 0,63\)

\(= 0,97\)

\(c)\) Xét biến cố \(\overline{N}\) của biến cố \(N\):

“Bạn Hương không được chọn vào tiết mục song ca”

\(\Rightarrow P(\overline{N}) = 1 \ – \ 0,9 = 0,1\)

Do \(C = E \cap \overline{N}\)

Suy ra \(P(C) = P(E). P(\overline{N}) = 0,7. 0,1 = 0,07\)

\(\)

Bài \(5\). Hai bạn Mai và Thi cùng tham gia một kì thi ngoại ngữ một cách độc lập nhau. Xác suất để bạn Mai và bạn Thi đạt từ điểm \(7\) trở lên lần lượt là \(0,8\) và \(0,9\). Tính xác suất của biến cố \(C\): “Cả hai bạn đều đạt từ điểm \(7\) trở lên.

Trả lời:

Xét hai biến cố:

\(A:\) “Bạn Mai thi được từ \(7\) điểm trở lên”

\(B:\) “Bạn Thi thi được từ \(7\) điểm trở lên”

Do \(C = A \cap B\)

\(\Rightarrow P(C) = P(A). P(B) = 0,8. 0,9 = 0,72\)

\(\)

Bài \(6\). Một người cho ngẫu nhiên \(3\) lá thư vào \(3\) chiếc phong bì đã ghi địa chỉ sao cho mỗi phong bì chỉ chứa một lá thư. Tính xác suất để có ít nhất một lá thư được cho vào đúng phong bì đã ghi địa chỉ theo lá thư đó.

Trả lời:

Số phần tử của không gian mẫu là:

\(n(\Omega) = 3! = 3. 2 . 1 = 6\)

Gọi \(A\) là biến cố: “Không lá thư nào được bỏ đúng phong bì”.

Suy ra biến cố \(\overline{A}\): “Có ít nhất một lá thứ được bỏ đúng phong bì”

Ta có: Số kết quả thuận lợi cho biến cố \(A\) là: \(n(A) = 2\)

\(\Rightarrow n(\overline{A}) = 1 \ – \ P(B) = 1 \ – \ \displaystyle \frac{2}{6} = \displaystyle \frac{2}{3}\)

Vậy xác suất để có ít nhất một lá thư được cho vào đúng phong bì đã ghi địa chỉ theo lá thư đó là \(\displaystyle \frac{2}{3}\)

\(\)

Bài \(7\). Một hộp có \(9\) quả cầu có cùng kích thước và khối lượng, trong đó có \(4\) quả cầu màu xanh đánh số từ \(1\) đến \(4\), có \(3\) quả cầu màu vàng đánh số từ \(1\) đến \(3\), có \(2\) quả cầu màu đỏ đánh số \(1\) và \(2\). Lấy ngẫu nhiên \(2\) quả cầu từ hộp. Tính xác suất để \(2\) quả cầu được lấy vừa khác màu, vừa khác số.

Trả lời:

Mỗi cách lấy ngẫu nhiên \(2\) quả cầu từ hộp \(9\) quả cầu là một tổ hợp chập \(2\) của \(9\) phần tử. Do đó, không gian mẫu \(\Omega\) gồm các tổ hợp chập \(2\) của \(9\) phần tử và:

\(n(\Omega) = C_9^2= 36\)

Số cách lấy ra \(2\) quả khác màu là:

Trường hợp \(1\): \(1\) quả màu xanh và \(1\) quả màu vàng, ta có số kết quả là: \(C_4^1. C_3^1 = 12\) cách

Trường hợp \(2\): \(1\) quả màu xanh và \(1\) quả màu đỏ, ta có số kết quả là: \(C_4^1. C_2^1 = 8\) cách

Trường hợp \(3\): \(1\) quả màu vàng và \(1\) quả màu đỏ, ta có số kết quả là: \(C_3^1. C_2^1 = 6\) cách

Suy ra tổng số cách lấy ra hai quả khác màu là:

\(12 + 8 + 6 = 26\) (cách)

Số cách lấy ra hai quả khác màu trùng số là:

Trường hợp \(1\): Hai qua lấy ra cùng là số \(1\), số cách là: \(C_3^2 = 3\)

Trường hợp \(2\): Hai qua lấy ra cùng là số \(2\), số cách là: \(C_3^2 = 3\)

Trường hợp \(3\): Hai qua lấy ra cùng là số \(3\), số cách là: \(C_2^2 = 1\)

Suy ra tổng số cách lấy ra hai quả khác màu trùng số là:

\(3 + 3 + 1 = 7\) (cách)

Do đó, số cách lấy ra hai quả khác màu khác số là:

\(26 \ – \ 7 = 19\) (cách)

Vậy xác suất để lấy ra hai quả khác màu, khác số là:

\(P = \displaystyle \frac{19}{36}\)

\(\)

Bài \(8\). Bạn An vẽ trên đất một bảng gồm \(9\) ô vuông như Hình \(3\). Sau đó, bạn An cầm \(4\) viên bi giống nhau đặt ngẫu nhiên vào \(4\) ô vuông trong bảng đó. Tính xác suất để bất kì hàng nào và cột nào của bảng cũng có viên bi.