ChÆ°ÆĄng 3 – BĂ i 2: HĂŹnh lÄng trỄ Äứng tam giĂĄc. HĂŹnh lÄng trỄ Äứng tứ giĂĄc trang 92 sĂĄch bĂ i táșp toĂĄn lá»p 7 táșp 1 NXB CĂĄnh Diá»u. CĂĄc em cĂčng Bumbii giáșŁi cĂĄc bĂ i táșp sau.
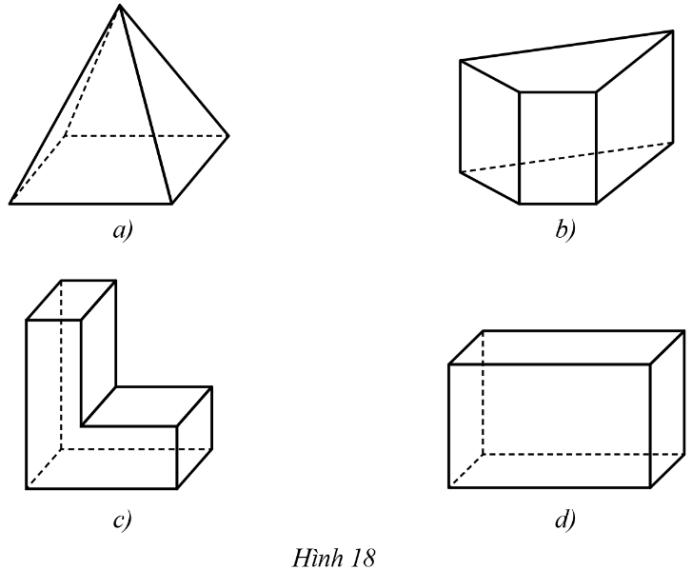
9. Trong cĂĄc hĂŹnh 18a, 18b, 18c, 18d cĂł hai hĂŹnh lÄng trỄ Äứng tứ giĂĄc. Chá» ra cĂĄc hĂŹnh lÄng trỄ Äứng tứ giĂĄc ÄĂł?
GiáșŁi
LÄng trỄ Äứng tứ giĂĄc cĂł: Hai máș·t ÄĂĄy cĂčng lĂ tứ giĂĄc vĂ song song vá»i nhau, cĂĄc máș·t bĂȘn lĂ hĂŹnh chữ nháșt.
Do ÄĂł hĂŹnh 18b, 18d lĂ hĂŹnh lÄng trỄ Äứng tứ giĂĄc.
\(\)
10. Trong cĂĄc phĂĄt biá»u sau, phĂĄt biá»u nĂ o ÄĂșng, phĂĄt biá»u nĂ o sai?
a) HĂŹnh lÄng trỄ Äứng tam giĂĄc cĂł 4 cáșĄnh, 6 Äá»nh.
b) HĂŹnh lÄng trỄ Äứng tam giĂĄc cĂł 5 máș·t, 5 Äá»nh.
c) HĂŹnh lÄng trỄ Äứng tam giĂĄc cĂł 4 máș·t, 5 Äá»nh.
d) HĂŹnh lÄng trỄ Äứng tam giĂĄc cĂł 5 máș·t, 6 Äá»nh.
GiáșŁi
a) lĂ phĂĄt biá»u sai vĂŹ hĂŹnh lÄng trỄ Äứng tam giĂĄc cĂł 9 cáșĄnh, 6 Äá»nh.
b) lĂ phĂĄt biá»u sai vĂŹ hĂŹnh lÄng trỄ Äứng tam giĂĄc cĂł 5 máș·t, 6 Äá»nh.
c) lĂ phĂĄt biá»u sai vĂŹ hĂŹnh lÄng trỄ Äứng tam giĂĄc cĂł 5 máș·t, 6 Äá»nh.
d) HĂŹnh lÄng trỄ Äứng tam giĂĄc cĂł 5 máș·t, 6 Äá»nh lĂ phĂĄt biá»u ÄĂșng.
Váșy trong cĂĄc phĂĄt biá»u trĂȘn, phĂĄt biá»u a, b, c lĂ phĂĄt biá»u sai; phĂĄt biá»u d lĂ phĂĄt biá»u ÄĂșng.
\(\)
11. Cho hĂŹnh lÄng trỄ Äứng tứ giĂĄc ABCD.A’B’C’D’ cĂł ÄĂĄy lĂ hĂŹnh thang ABCD vuĂŽng táșĄi B (AB song song vá»i CD) vá»i AB = 9 dm, DC = 6 dm, BC = 4 dm, AD = 5 dm vĂ chiá»u cao AA’ = 100 cm (HĂŹnh 19).
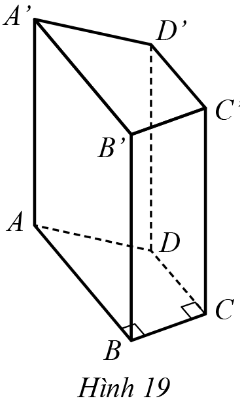
a) TĂnh diá»n tĂch xung quanh của hĂŹnh lÄng trỄ ABCD.A’B’C’D’.
b) TĂnh thá» tĂch của hĂŹnh lÄng trỄ ABCD.A’B’C’D’.
c) NgÆ°á»i ta dĂĄn giáș„y mĂ u (bĂȘn ngoĂ i) táș„t cáșŁ cĂĄc máș·t của hĂŹnh lÄng trỄ. TĂnh sá» tiá»n ngÆ°á»i ÄĂł pháșŁi tráșŁ, biáșżt ráș±ng giĂĄ tiá»n dĂĄn giáș„y mĂ u má»i mĂ©t vuĂŽng (bao gá»m tiá»n cĂŽng vĂ nguyĂȘn váșt liá»u) lĂ 150 000 Äá»ng.
GiáșŁi
a) Äá»i \(100\) cm \(= 10\) dm.
Diá»n tĂch xung quanh của hĂŹnh lÄng trỄ ABCD.A’B’C’D’ lĂ :
\((9 + 6 + 4 + 5) . 10 = 240\) (dm2).
b) Diá»n tĂch ÄĂĄy ABCD của hĂŹnh lÄng trỄ lĂ :
\(\displaystyle\frac{(9+6).4}{2} = 30\) (dm2).
Thá» tĂch của hĂŹnh lÄng trỄ ABCD.A’B’C’D’ lĂ :
\(30. 10 = 300\) (dm3).
c) Tá»ng diá»n tĂch táș„t cáșŁ cĂĄc máș·t của hĂŹnh lÄng trỄ lĂ :
\(240 + 2.30 = 300\) (dm2) \(= 3\) (m2).
Sá» tiá»n ngÆ°á»i ÄĂł pháșŁi tráșŁ lĂ :
\(3. 150\ 000 = 450\ 000\) (Äá»ng).
\(\)
12. Cho hĂŹnh lÄng trỄ Äứng tam giĂĄc ABC.DEG cĂł ÄĂĄy lĂ tam giĂĄc ABC vuĂŽng táșĄi B vá»i cáșĄnh ÄĂĄy AB = 2 cm vĂ cáșĄnh bĂȘn AD = 5 cm (HĂŹnh 20). TĂnh Äá» dĂ i cáșĄnh BC, biáșżt thá» tĂch của hĂŹnh lÄng trỄ ÄĂł báș±ng 25 cm3.
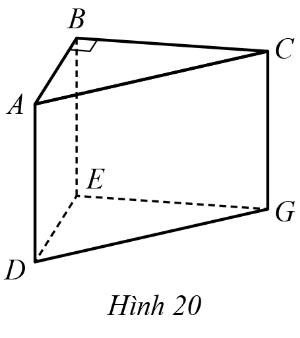
GiáșŁi
Diá»n tĂch ÄĂĄy \(ABC\) của hĂŹnh lÄng trỄ lĂ :
\(S_{ABC}=25 : 5 = 5\) (cm2).
Do ÄĂł Äá» dĂ i cáșĄnh \(BC\) lĂ :
\(BC = (S_{ABC}.2):AB=(5.2):2=5\) (cm).
Váșy Äá» dĂ i cáșĄnh \(BC\) lĂ \(5\) cm.
\(\)
13. Cho hĂŹnh lÄng trỄ Äứng tứ giĂĄc ABCD.MNPQ cĂł ÄĂĄy lĂ hĂŹnh thang ABCD vuĂŽng táșĄi B (AD song song vá»i BC) vá»i AB = 20 cm, AD = 11 cm, BC = 15 cm (HĂŹnh 21).
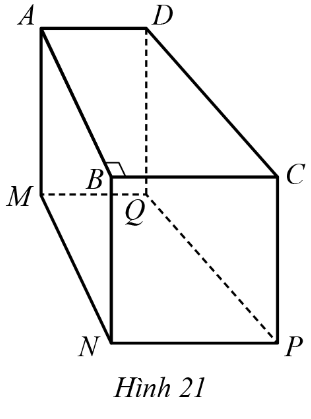
a) TĂnh tá» sá» giữa thá» tĂch của hĂŹnh lÄng trỄ Äứng tam giĂĄc ABC.MNP vĂ thá» tĂch của hĂŹnh lÄng trỄ Äứng tứ giĂĄc ABCD.MNPQ.
b) TĂnh tá» sá» pháș§n trÄm giữa thá» tĂch của hĂŹnh lÄng trỄ Äứng tam giĂĄc ABD.MNQ vĂ thá» tĂch của hĂŹnh lÄng trỄ Äứng tam giĂĄc BCD.NPQ.
c) So sĂĄnh thá» tĂch của hai hĂŹnh lÄng trỄ Äứng tam giĂĄc ABD.MNQ vĂ ACD.MPQ.
GiáșŁi
a) Diá»n tĂch ÄĂĄy tam giĂĄc \(ABC\) lĂ :
\(S_{ABC} = \displaystyle\frac{1}{2}AB.BC = \displaystyle\frac{1}{2}.20.15 = 150\) (cm2).
Diá»n tĂch ÄĂĄy hĂŹnh thang \(ABCD\) lĂ :
\(S_{ABCD} = \displaystyle\frac{(AD + BC).AB}{2} = \displaystyle\frac{(11 + 15).20}{2} = 260\) (cm2).
Tá» sá» giữa thá» tĂch của hĂŹnh lÄng trỄ Äứng tam giĂĄc \(ABC.MNP\) vĂ thá» tĂch của hĂŹnh lÄng trỄ Äứng tứ giĂĄc \(ABCD.MNPQ\) lĂ :
\(\displaystyle\frac{V_{ABC.MNP}}{V_{ABCD.MNPQ}}=\displaystyle\frac{S_{ABC}.BN}{S_{ABCD}.BN}\) \(=\displaystyle\frac{S_{ABC}}{S_{ABCD}}=\displaystyle\frac{150}{260}=\displaystyle\frac{15}{26}.\)
Váșy tá» sá» cáș§n tĂŹm báș±ng \(\displaystyle\frac{15}{26}.\)
b) Diá»n tĂch ÄĂĄy tam giĂĄc \(ABD\) lĂ :
\(S_{ABD} = \displaystyle\frac{AB.AD}{2} = \displaystyle\frac{20.11}{2} = 110\) (cm2).
Diá»n tĂch ÄĂĄy tam giĂĄc \(BCD\) lĂ :
\(S_{BCD} = \displaystyle\frac{AB.BC}{2} = \displaystyle\frac{20.15}{2} = 150\) (cm2).
Tá» sá» pháș§n trÄm giữa thá» tĂch của hĂŹnh lÄng trỄ Äứng tam giĂĄc \(ABD.MNQ\) vĂ thá» tĂch của hĂŹnh lÄng trỄ Äứng tam giĂĄc \(BCD.NPQ\) lĂ :
\(\displaystyle\frac{V_{BCD.MNP.100\%}}{V_{BCD.NPQ}}=\displaystyle\frac{S_{ABD}.BN.100\%}{S_{BCD}.BN}\) \(=\displaystyle\frac{S_{ABD.100\%}}{S_{BCD}}=\displaystyle\frac{110.100\%}{150}=73,(3)\)
Váșy tá» sá» pháș§n trÄm cáș§n tĂŹm báș±ng \(73,(3)\%.\)
c) Thá» tĂch của hai hĂŹnh lÄng trỄ Äứng tam giĂĄc \(ABD.MNQ\) vĂ \(ACD.MPQ\) báș±ng nhau do diá»n tĂch hai ÄĂĄy \(ABD,\ ACD\) báș±ng nhau vĂ chĂșng cĂł cĂčng chiá»u cao \(BN.\)
\(\)
14. SáșŻp xáșżp cĂĄc hĂŹnh sau theo thứ tá»± thá» tĂch giáșŁm dáș§n:
â HĂŹnh lÄng trỄ Äứng tứ giĂĄc cĂł Äá» dĂ i cáșĄnh bĂȘn báș±ng 10 cm vĂ ÄĂĄy lĂ hĂŹnh thang cĂąn vá»i Äá» dĂ i ÄĂĄy bĂ©, ÄĂĄy lá»n, ÄÆ°á»ng cao láș§n lÆ°á»Łt báș±ng 2 cm, 8 cm, 4 cm;
â HĂŹnh láșp phÆ°ÆĄng cĂł Äá» dĂ i cáșĄnh báș±ng 8 cm;
â HĂŹnh lÄng trỄ Äứng tam giĂĄc cĂł Äá» dĂ i cáșĄnh bĂȘn báș±ng 10 cm vĂ ÄĂĄy lĂ tam giĂĄc cĂł Äá» dĂ i má»t cáșĄnh, ÄÆ°á»ng cao tÆ°ÆĄng ứng cáșĄnh ÄĂł láș§n lÆ°á»Łt báș±ng 4 cm, 3 cm.
GiáșŁi
Diá»n tĂch hĂŹnh lÄng trỄ Äứng tứ giĂĄc lĂ :
\(\displaystyle\frac{1}{2}.(2 + 8).4 = 20\) (cm2).
Thá» tĂch của hĂŹnh lÄng trỄ Äứng tứ giĂĄc lĂ :
\(20.10 = 200\) (cm3).
Thá» tĂch của hĂŹnh láșp phÆ°ÆĄng lĂ :
\(8^3 = 512\) (cm3).
Thá» tĂch của hĂŹnh lÄng trỄ Äứng tam giĂĄc lĂ :
\(\displaystyle\frac{4.3}{2}.10 = 6\) (cm2).
Do \(512 > 200 > 60\) nĂȘn sáșŻp xáșżp cĂĄc hĂŹnh theo thứ tá»± thá» tĂch giáșŁm dáș§n lĂ : hĂŹnh láșp phÆ°ÆĄng, hĂŹnh lÄng trỄ Äứng tứ giĂĄc, hĂŹnh lÄng trỄ Äứng tam giĂĄc.
\(\)
15*. NgÆ°á»i ta ghi má»t cĂĄch tuỳ Ăœ vĂ o ba máș·t bĂȘn vĂ hai máș·t ÄĂĄy của hĂŹnh lÄng trỄ Äứng tam giĂĄc cĂĄc sá» tá»± nhiĂȘn láș» từ 21 Äáșżn 29 (sá» ÄÆ°á»Łc ghi á» má»i máș·t khĂĄc nhau). Chứng tá» ráș±ng khĂŽng thá» xáșŁy ra trÆ°á»ng hợp tá»ng cĂĄc sá» trĂȘn ba máș·t bĂȘn vĂ tá»ng cĂĄc sá» trĂȘn hai ÄĂĄy của hĂŹnh lÄng trỄ trĂȘn báș±ng nhau.
GiáșŁi
Do tá»ng của ba sá» láș» lĂ má»t sá» láș» nĂȘn tá»ng cĂĄc sá» trĂȘn ba máș·t bĂȘn của hĂŹnh lÄng trỄ lĂ má»t sá» láș».
MĂ tá»ng của hai sá» láș» lĂ má»t sá» cháș”n nĂȘn tá»ng cĂĄc sá» trĂȘn hai ÄĂĄy của hĂŹnh lÄng trỄ lĂ má»t sá» cháș”n.
Do ÄĂł khĂŽng thá» xáșŁy ra trÆ°á»ng hợp tá»ng cĂĄc sá» trĂȘn ba máș·t bĂȘn vĂ tá»ng cĂĄc sá» trĂȘn hai ÄĂĄy của hĂŹnh lÄng trỄ trĂȘn báș±ng nhau.
\(\)
Xem bĂ i giáșŁi trÆ°á»c: BĂ i 1: HĂŹnh há»p chữ nháșt. HĂŹnh láșp phÆ°ÆĄng
Xem bĂ i giáșŁi tiáșżp theo: BĂ i táșp cuá»i chÆ°ÆĄng 3
Xem thĂȘm cĂĄc bĂ i giáșŁi khĂĄc táșĄi: GiáșŁi BĂ i táșp ToĂĄn Lá»p 7 CĂĄnh Diá»u
ThĂŽng tin liĂȘn há» & máșĄng xĂŁ há»i:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech
