Bài tập cuối chương \(IV\) trang \(102\) SGK Toán lớp \(11\) tập \(1\) Kết nối tri thức với cuộc sống. Các em cùng Bumbii giải các bài tập sau:
\(A\) – TRẮC NGHIỆM
Bài \(4.35\). Cho đường thẳng \(a\) song song với mặt phẳng \((P)\). Mặt phẳng \((Q)\) chứa đường thẳng \(a\) và cắt mặt phẳng \((P)\) theo giao tuyến là đường thẳng \(b\). Vị trí tương đối của hai đường thẳng \(a\) và \(b\) là:
\(A\). Chéo nhau.
\(B\). Cắt nhau.
\(C\). Song song.
\(D\). Trùng nhau.
Trả lời:
Chọn đáp án \(C\).
\(\)
Bài \(4.36\). Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(M\) là trung điểm của cạnh \(SD\). Đường thẳng \(SB\) song song với mặt phẳng:
\(A\). \((CDM)\).
\(B\). \((ACM)\).
\(C\). \((ADM)\).
\(D\). \((ACD)\).
Trả lời:
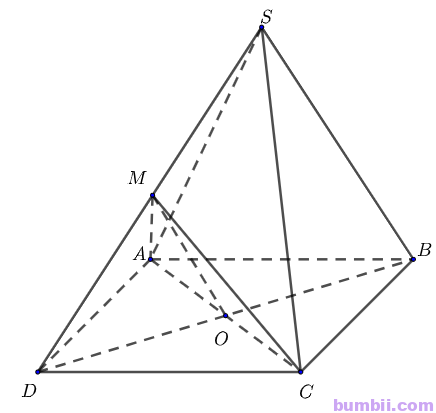
Gọi \(O\) là giao điểm hai đường chéo \(AC\) và \(BD\). Khi đó, \(O\) là trung điểm mỗi đường.
Xét tam giác \(SBD\) có \(M, O\) lần lượt là trung điểm của \(SD, BD\) nên \(MO\) là đường trung bình của tam giác \(SBD\)
Suy ra \(MO // SB\) (\(1\))
Có \(O \in AC\) nên \(O \in (ACM)\). Mà \(M \in (ACM)\)
Do đó, \(OM\) nằm trong mặt phẳng \((ACM)\). (\(2\))
Từ (\(1\)) và (\(2\)) suy ra:
\(SB // (ACM)\)
Chọn đáp án \(B\).
\(\)
Bài \(4.37\). Cho hình hộp \(ABCD.A’B’C’D’\). Mặt phẳng \((AB’D’)\) song song với mặt phẳng
\(A\). \((ABCD)\).
\(B\). \((BCC’B’)\).
\(C\). \((BDA’)\).
\(D\). \((BDC’)\).
Trả lời:
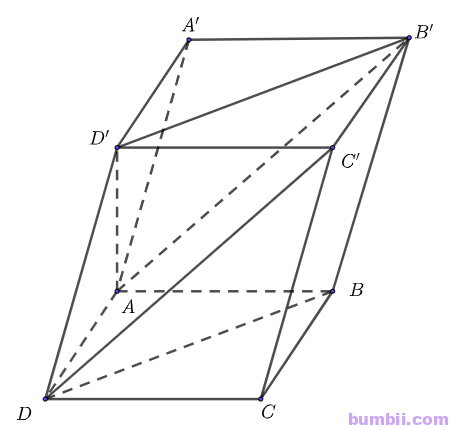
\(ABCD.A’B’C’D’\) là hình hộp nên các mặt là các hình bình hành và các cạnh bên \(AA’, BB’, CC’, DD’\) đôi một song song.
Xét tứ giác \(BDD’B’\) có \(BB’ // DD’\) và \(BB’ = DD’\) nên tứ giác \(BDD’B’\) là hình bình hành.
\(\Rightarrow B’D’ // BD\)
\(\Rightarrow B’D’ // (BDC’)\)
Ta lại có: \(A’B’C’D’\) là hình bình hành nên \(A’B’ // C’D’, A’B’ = C’D’\) (\(1\))
\(ABB’A’\) là hình bình hành nên \(A’B’ // AB, A’B’ = AB\) (\(2\))
(\(1\)) và (\(2\)) suy ra: \(AB // C’D’, AB = C’D’\)
hay tứ giác \(ABC’D’\) là hình bình hành.
\(\Rightarrow AD’ // BC’\)
\(\Rightarrow AD’ // (BDC’)\)
Mặt phẳng \((ABD’)\) chứa hai đường thẳng cắt nhau \(B’D’\) và \(AD’\) cùng song song với mặt phẳng \((BDC’)\) nên \((ABD’) // (BDC’)\)
Chọn đáp án \(D\)
\(\)
Bài \(4.38\). Cho ba mặt phẳng \((P), (Q), (R)\) đôi một song song với nhau. Đường thẳng \(a\) cắt các mặt phẳng \((P), (Q), (R)\) lần lượt tại \(A, B, C\) sao cho \(\displaystyle \frac{AB}{BC} = \displaystyle \frac{2}{3}\) và đường thẳng \(b\) cắt các mặt phẳng \((P), (Q), (R)\) lần lượt tại \(A’, B’, C’\). Tỉ số \(\displaystyle \frac{A’B’}{B’C’}\) bằng
\(A\). \(\displaystyle \frac{2}{3}\).
\(B\). \(\displaystyle \frac{1}{2}\).
\(C\). \(\displaystyle \frac{3}{2}\).
\(D\). \(\displaystyle \frac{2}{5}\).
Trả lời:
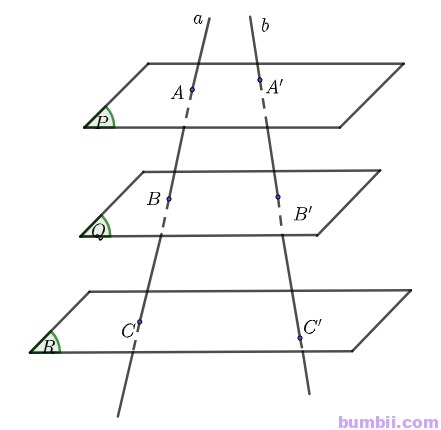
Theo định lý Thales trong không gian ta có:
\(\displaystyle \frac{AB}{A’B’} = \displaystyle \frac{BC}{B’C’} = \displaystyle \frac{AC}{A’C’}\)
Suy ra \(\displaystyle \frac{A’B’}{B’C’} = \displaystyle \frac{AB}{BC} = \displaystyle \frac{2}{3}\)
Chọn đáp án \(A\).
\(\)
Bài \(4.39\). Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(M, N\) lần lượt là trung điểm của các cạnh \(SB, SD\); \(K\) là giao điểm của mặt phẳng \((AMN)\) và đường thẳng \(SC\). Tỉ số \(\displaystyle \frac{SK}{SC}\) bằng
\(A\). \(\displaystyle \frac{1}{2}\).
\(B\). \(\displaystyle \frac{1}{3}\).
\(C\). \(\displaystyle \frac{1}{4}\).
\(D\). \(\displaystyle \frac{2}{3}\).
Trả lời:
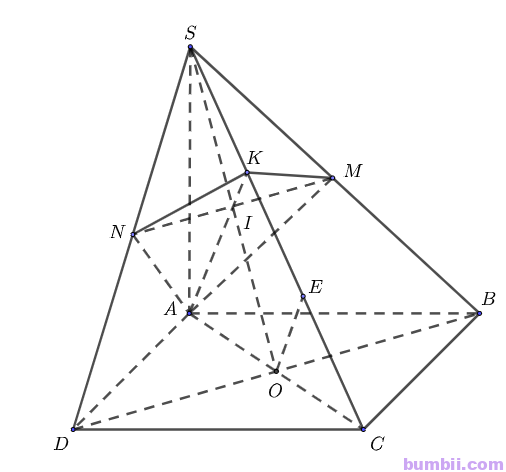
Gọi \(O\) là giao điểm hai đường chéo \(AC\) và \(BD\) của hình bình hành \(ABCD\).
Xét trong mặt phẳng \((SBD)\), gọi \(I\) là giao điểm của \(SO\) và \(MN\).
Xét trong mặt phẳng \((SAC)\), gọi \(K\) là giao điểm của \(AI\) và \(SC\).
Vì \(K \in AI\) mà \(AI\) nằm trong \((AMN)\) nên \(K \in (AMN)\). Lại có \(K \in SC\)
Suy ra \(K\) là giao điểm của \(SC\) và mặt phẳng \((AMN)\).
Xét tam giác \(SBD\) có \(MN\) là đường trung bình nên \(MN // BD\)
\(\Rightarrow NI // BD\)
\(\Rightarrow NI // BO\)
Xét tam giác \(SDO\) có \(NS = ND\) và \(NI // BO\)
Suy ra \(I\) là trung điểm \(SO\)
Trong mặt phẳng \((SAC)\), kẻ \(OE // AK (E \in SC)\)
Xét tam giác \(SOC\) có \(IK // OE\), \(I\) là trung điểm \(SO\) nên \(K\) là trung điểm \(SE\) hay \(\displaystyle \frac{SK}{SE} = \displaystyle \frac{1}{2}\) (\(1\))
Xét tam giác \(ACK\) có \(O\) là trung điểm \(AC\) và \(OE // AK\) nên \(\displaystyle \frac{CE}{CK} = \displaystyle \frac{CO}{AC} = \displaystyle \frac{1}{2}\) (\(2\))
Từ (\(1\)) và (\(2\)) ta có:
\(SK = KE = EC\).
Suy ra \(\displaystyle \frac{SK}{SC} = \displaystyle \frac{1}{3}\)
Chọn đáp án \(B\)
\(\)
Bài \(4.40\). Cho hình hộp \(ABCD.A’B’C’D’\). Gọi \(M, M’\) lần lượt là trung điểm của các cạnh \(BC, B’C’\). Hình chiếu của \(\Delta{B’DM}\) qua phép chiếu song song trên \((A’B’C’D’)\) theo phương chiếu \(AA’\) là
\(A\). \(\Delta B’A’M\).
\(B\). \(\Delta C’D’M’\).
\(C\). \(\Delta DMM’\).
\(D\). \(\Delta B’D’M’\).
Trả lời:
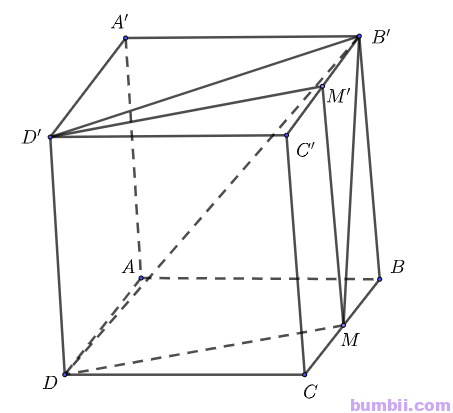
\(ABCD.A’B’C’D’\) là hình hộp nên các mặt bên là các hình bình hành và các cạnh bên \(AA’, BB’, CC’, DD’\) đôi một song song.
Do \(DD’ // AA’\) nên \(D’\) là hình chiếu song song của \(D\) lên mặt phẳng \((A’B’C’D’)\) theo phương chiếu \(AA’\)
\(B’\) là hình chiếu song song của chính nó trên mặt phẳng \((A’B’C’D’)\) theo phương chiếu \(AA’\).
Xét hình bình hành \(BCC’B’\) có \(M, M’\) lần lượt là trung điểm \(BC, B’C’\) nên \(MM’\) là đường trung bình của hình bình hành \(BCC’B’\)
\(\Rightarrow MM’ // CC’ // AA’\)
Suy ra \(M’\) là hình chiếu song song của điểm \(M\) lên mặt phẳng \((A’B’C’D’)\) theo phương chiếu \(AA’\).
Vậy, tam giác \(B’D’M’\) chính là hình chiếu của tam giác \(B’DM\) qua phép chiếu song song lên mặt phẳng \((A’B’C’D’)\) theo phương chiếu \(AA’\).
\(\)
\(B\) – TỰ LUẬN
Bài \(4.41\). Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang, \(AB // CD\) và \(AB < CD\). Xác định giao tuyến của hai mặt phẳng
\(a)\) \((SAD) \text{ và } (SBC)\);
\(b)\) \((SAB) \text{ và } (SCD)\);
\(c)\) \((SAC) \text{ và } (SBD)\).
Trả lời:
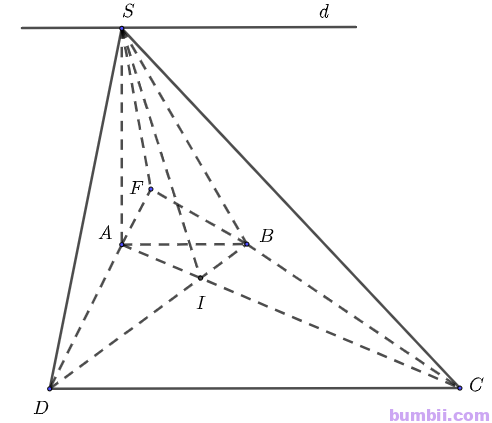
\(a)\) Xét mặt phẳng \((ABCD)\), gọi \(F\) là giao điểm của \(AD\) và \(BC\)
Khi đó, \(F \in AD\) nên \(F \in (SAD)\)
\(F \in BC\) nên \(F \in (SBC)\).
Khi đó \(F\) là điểm chung của hai mặt phẳng \((SAD)\) và \((SBC)\).
Lại có \(S\) cũng là điểm chung của hai mặt phẳng \((SAD)\) và \((SBC)\).
Vậy \(SF\) là giao tuyến của hai mặt phẳng \((SAD)\) và \((SBC)\)
\(b)\) Hai mặt phẳng \((SAB)\) và \((SCD)\) lần lượt chứa hai đường thẳng \(AB\) và \(CD\) song song với nhau. Khi đó, giao tuyến của hai mặt phẳng là đường thẳng đi qua điểm chung \(S\) và song song với \(AB, CD\).
Qua \(S\) ta vẽ đường thẳng \(d\) song song với \(AB\) và \(CD\).
Khi đó \(d\) là giao tuyến của hai mặt phẳng \((SAB)\) và \((SCD)\).
\(c)\) Trong mặt phẳng \((ABCD)\), gọi \(I\) là giao điểm của \(AC\) và \(BD\).
Khi đó, \(I\) thuộc \(AC\) nên \(I \in (SAC)\)
\(I\) thuộc \(BD\) nên \(I \in (SBD)\)
\(\Rightarrow I\) là điểm chung của hai mặt phẳng \((SAC)\) và \((SBD)\).
Lại có, \(S\) cũng là \(1\) điểm chung của hai mặt phẳng \((SAC)\) và \((SBD)\).
Vậy \(SI\) là giao tuyến của hai mặt phẳng \((SAC)\) và \((SBD)\).
\(\)
Bài \(4.42\). Cho hình lăng trụ tam giác \(ABC.A’B’C’\). Gọi \(M, N, P\) lần lượt là trung điểm của các cạnh \(AB, BC\) và \(AA’\).
\(a)\) Xác định giao điểm của mặt phẳng \((MNP)\) với đường thẳng \(B’C\).
\(b)\) Gọi \(K\) là giao điểm của mặt phẳng \((MNP)\) với đường thẳng \(B’C\). Tính tỉ số \(\displaystyle \frac{KB’}{KC}\).
Trả lời:
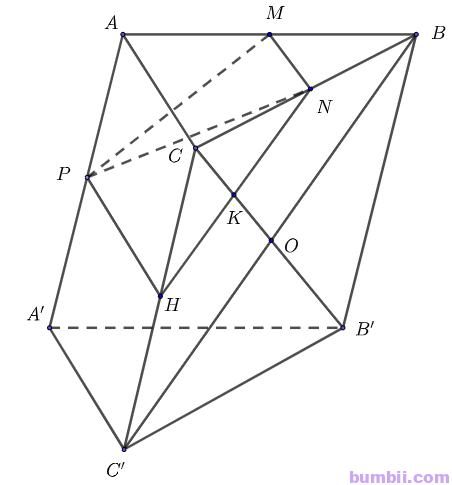
Ta có \((MNP) \cap (ABC) = MN, (ABC) \cap (ACC’A’) = AC\)
Mà \(AC // MN\) (do \(MN\) là đường trung bình của tam giác \(ABC\)).
Suy ra giao tuyến của hai mặt phẳng \((MNP)\) và \((ACC’A’)\) là đường thẳng qua \(P\) và song song với \(MN\) và \(AC\).
Qua \(P\) kẻ \(PH // AC (H \in CC’)\)
Khi đó \(PH\) là giao tuyến của \((MNP)\) và \((ACC’A’)\).
Xét trong mặt phẳng \((BCC’B’)\), nối \(H\) với \(N\) cắt \(B’C\) tại \(K\).
Vậy \(K\) là giao điểm của \((MNP)\) với \(B’C\).
\(b)\) Gọi \(O\) là giao điểm của \(BC’\) và \(B’C\). Khi đó \(OC = OB’\)
Xét hình bình hành \(ACC’A’\) có \(P\) là trung điểm \(AA’\), \(PH // AC\) suy ra \(H\) là trung điểm \(CC’\).
Xét tam giác \(BCC’\) có \(H, N\) lần lượt là trung điểm của \(CC’\) và \(CB\) nên \(HN\) là đường trung bình của tam giác \(BCC’\)
\(\Rightarrow HN // BC’\)
\(\Rightarrow \displaystyle \frac{KC}{CO} = \displaystyle \frac{CH}{CC’} = \displaystyle \frac{1}{2}\)
\(\Rightarrow KC = KO\)
Suy ra \(\displaystyle \frac{KB’}{KC} = \displaystyle \frac{KO + OB’}{KO} = \displaystyle \frac{3KO}{KO} = 3\)
\(\)
Bài \(4.43\). Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Trên cạnh \(SC\) và cạnh \(AB\) lần lượt lấy điểm \(M\) và \(N\) sao cho \(CM = 2 SM, BN = 2 AN\)
\(a)\) Xác định giao điểm \(K\) của mặt phẳng \((ABM)\) với đường thẳng \(SD\). Tính tỉ số \(\displaystyle \frac{SK}{SD}\).
\(b)\) Chứng minh rằng \(MN // (SAD)\).
Trả lời:
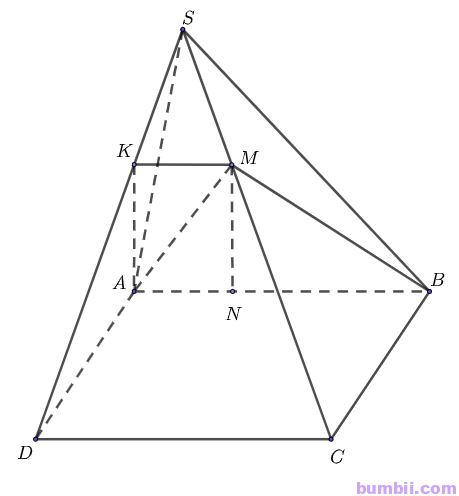
Ta có: \((ABM) \cap (ABCD) = AB, (ABCD) \cap (SCD) = CD\)
Mà \(CD // AB\) nên giao tuyến của hai mặt phẳng \((ABM)\) và \((SCD)\) là đường thẳng qua \(M\) và song song với \(AB\) và \(CD\).
Qua \(M\) kẻ \(MK // CD, K \in SD\)
Vậy \(K\) là giao điểm của \((AMN)\) với \(SD\).
Xét tam giác \(SCD\) có \(MK // CD\) nên:
\(\displaystyle \frac{SK}{SD} = \displaystyle \frac{SM}{SC} = \displaystyle \frac{1}{3}\)
\(b)\) Tam giác \(SCD\) có \(MK // CD\) nên:
\(\displaystyle \frac{KM}{CD} = \displaystyle \frac{SM}{SC} = \displaystyle \frac{1}{3}\)
Mặt khác \(\displaystyle \frac{AN}{AB} = \displaystyle \frac{AN}{AN + BN} = \displaystyle \frac{1}{3}\)
Mà \(AB = CD\) suy ra:
\(MK = AN\)
Tứ giác \(MNAK\) có \(MK // AN\) (cùng song song với \(AD\)) và \(MK = AN\) nên tứ giác \(MNAK\) là hình bình hành.
Suy ra \(MN // AK\)
Lại có \(AK \subset (SAD)\)
Vậy \(MN // (SAD)\)
\(\)
Bài \(4.44\). Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(G, K\) lần lượt là trọng tâm của các tam giác \(SAD, SCD\).
\(a)\) Chứng minh rằng \(GK // (ABCD)\).
\(b)\) Mặt phẳng chứa đường thẳng \(GK\) và song song với mặt phẳng \((ABCD)\) cắt các cạnh \(SA, SB, SC, SD\) lần lượt tại \(M, N, E, F\). Chứng minh rằng tứ giác \(MNEF\) là hình bình hành.
Trả lời:
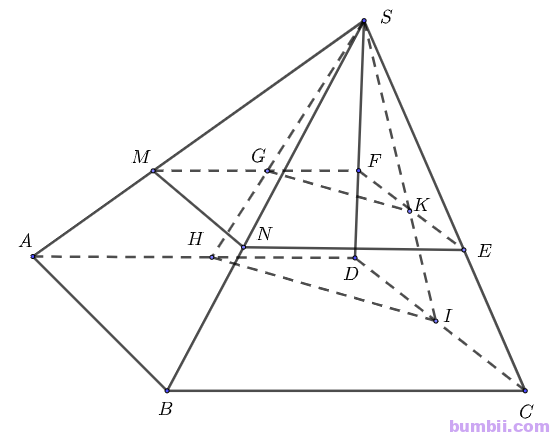
\(a)\) Gọi \(H, I\) lần lượt là trung điểm \(AD, CD\)
\(\Rightarrow GS = 2 GH, KS = 2 KI\)
Suy ra \(GK // HI\). Mà \(HI \subset (ABCD)\)
Vậy \(GK // (ABCD)\).
\(b)\) Trong mặt phẳng \((SAD)\), qua \(G\) vẽ đường thẳng song song với \(AD\), cắt \(SA, SD\) lần lượt tại \(M, F\).
Trong mặt phẳng \((SCD)\), nối \(F\) và \(K\) cắt \(SC\) tại \(E\).
Trong mặt phẳng \((SBC)\), qua \(E\) kẻ đường thẳng song song với \(BC\) cắt \(SB\) tại \(N\).
Ta được mặt phẳng \((MNEF)\) song song với \((ABCD)\)
Xét tam giác \(SAD\) có \(MF // AD\) nên:
\(\displaystyle \frac{MF}{AD} = \displaystyle \frac {SF}{SD}\) (\(1\))
Xét tam giác \(SCD\) có \(EF // CD\) nên:
\(\displaystyle \frac{SE}{SC} = \displaystyle \frac{SF}{SD}\) (\(2\))
Xét tam giác \(SBC\) có \(NE // BC\) nên:
\(\displaystyle \frac{NE}{BC} = \displaystyle \frac{SC}{SC}\) (\(3\))
Từ (\(1\)), (\(2\)) và (\(3\)) suy ra:
\(\displaystyle \frac{MF}{AD} = \displaystyle \frac{NE}{BC}\)
Mà \(BC // AD, BC = AD\) nên ta có \(MF // NE. MF = NE\)
Suy ra tứ giác \(MNEF\) là hình bình hành.
\(\)
Bài \(4.45\). Cho hình hộp \(ABCD.A’B’C’D’\). Gọi \(M, N\) lần lượt là trung điểm của cạnh \(AD, A’B’\). Chứng minh rằng:
\(a)\) \(BD // B’D’, (A’BD) // (CB’D’)\) và \(MN // (BDD’B’)\).
\(b)\) Đường thẳng \(AC’\) đi qua trọng tâm \(G\) của tam giác \(A’BD\).
Trả lời:
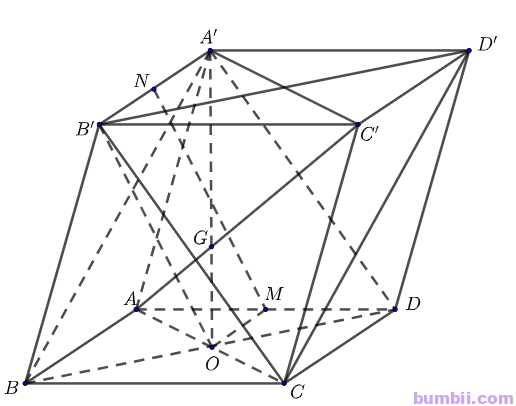
\(a)\) Ta có \(ABCD.A’B’C’D’\) là hình hộp nên các mặt bên là các hình bình hành, các cạnh bên \(AA, BB’, CC’, DD’\) song song với nhau từng đôi một và \((ABCD) // (A’B’C’D’)\).
Mà \((ABCD) \cap (BDD’B’) = BD\), \((A’B’C’D’) \cap (BDD’B’) = B’D’\)
\(\Rightarrow BD // B’D’\)
\(\Rightarrow BD // (CB’D’)\).
Chứng minh tương tự, ta có \(A’B // CD’\) nên \(A’B // (CB’D’)\)
Mặt phẳng \((A’BD)\) chứa hai đường thẳng \(A’B\) và \(BD\) cắt nhau và cùng song song với mặt phẳng \((CB’D’)\) nên \((A’BD) // (CB’D’)\).
Gọi \(O\) là giao điểm hai đường chéo \(AC\) và \(BD\) của hình bình hành \(ABCD\). Khi đó \(O\) là trung điểm mỗi đường.
Có \(O, M\) lần lượt là trung điểm \(AC, AD\) nên \(OM // CD, OM = \displaystyle \frac{1}{2} CD\).
Lại có \(N\) là trung điểm \(A’B’\) suy ra:
\(B’N = \displaystyle \frac{1}{2} A’B’ = \displaystyle \frac{1}{2} CD\) và \(B’N // CD\)
Xét tứ giác \(OMNB’\) có:
\(B’N = OM\) và \(B’N // OM (\text{ cùng } // CD)\) nên tứ giác \(OMNB’\) là hình bình hành.
\(\Rightarrow MN // OB’\)
Mà \(OB’ \subset (BDD’B’)\) suy ra \(MN // (BDD’B’)\).
\(b)\) Gọi \(O\) là giao điểm của \(AC’\) và \(A’O\).
Ta có: \(AO // A’C’\) và \(AO = \displaystyle \frac{1}{2} A’C’\) nên suy ra:
\(\displaystyle \frac{AO}{A’C’} = \displaystyle \frac{OG}{A’G} = \displaystyle \frac{1}{2}\)
Lại có \(O\) là trung điểm \(BD\)
Suy ra \(G\) là trọng tâm tam giác \(A’BD\)
Vậy đường thẳng \(AC’\) đi qua trọng tâm \(G\) của tam giác \(A’BD\).
\(\)
Bài \(4.46\). Cho tứ diện \(ABCD\). Trên cạnh \(AB\) lấy điểm \(M\) sao cho \(BM = 3AM\). Mặt phẳng \((P)\) đi qua \(M\) song song với hai đường thẳng \(AD\) và \(BC\).
\(a)\) Xác định giao điểm \(K\) của mặt phẳng \((P)\) với đường thẳng \(CD\).
\(b)\) Tính tỉ số \(\displaystyle \frac{KC}{CD}\).
Trả lời:
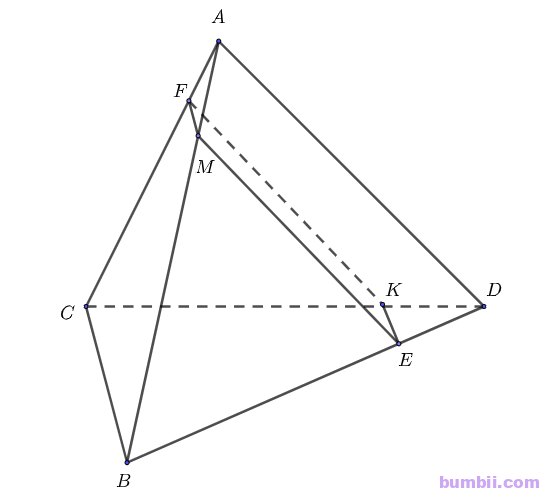
\(a)\) Qua \(M\) kẻ \(MH // BC, MI // AD\).
Mặt phẳng \((P)\) đi qua \(M\) và song song với \(BC\) và \(AD\) nên mặt phẳng \((P)\) chứa \(MH\) và \(MI\).
\((P) \cap (ABC) = MH, (ABC) \cap (BCD) = BC\)
Mà \(MH // BC\) nên giao tuyến của \((P)\) với \((BCD)\) song song với \(BC\) và \(MH\).
Qua \(I\) kẻ \(IK // BC (K \in CD)\)
Vậy \(K\) là giao điểm của \((P)\) với \(CD\).
\(b)\) Có \((P) \cap (ABD) = MI, (P) \cap (ACD) = HK\), \((ABD) \cap (ACD) = AD\)
Mà \(MI // AD\)
Suy ra \(HK // MI\)
Tứ giác \(MHKI\) có \(MH // KI, MI // HK\) nên tứ giác \(MHKI\) là hình bình hành.
Do đó \(MH = KI\)
Xét tam giác \(ABC\) có \(MH // BC\) nên ta có:
\(\displaystyle \frac{MH}{BC} = \displaystyle \frac{AM}{AB} = \displaystyle \frac{AM}{AM + BM}\)
\(= \displaystyle \frac{AM}{4AM} = \displaystyle \frac{1}{4}\)
\(\Rightarrow BC = 4 MH = 4 KI\)
Xét tam giác \(BCD\) có \(IK //BC, BC = 4 KI\). Suy ra:
\(\displaystyle \frac{KC}{CD} = \displaystyle \frac{3}{4}\)
Bài tập cuối chương IV Bài tập cuối chương IV Bài tập cuối chương IV Bài tập cuối chương IV Bài tập cuối chương IV Bài tập cuối chương IV
Xem bài giải trước: Bài 14 – Phép chiếu song song
Xem bài giải tiếp theo: Bài 15 – Giới hạn của dãy số
Xem các bài giải khác: Giải bài tập SGK Toán Lớp 11 Kết nối tri thức với cuộc sống
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech

Hạnh phúc đạt được khi bạn ngừng chờ đợi điều đó xảy ra và thực hiện các bước để biến nó thành hiện thực.